Способ представления числа символами некоторого алфавита которые называются цифрами

СИСТЕМА СЧИСЛЕНИЯ – способ представления числа символами некоторого алфавита, которые называют цифрами.

Простейшая и самая древняя – так называемая унарная система счисления. В ней для записи любых чисел (т.е. кодирования) используется один символ: палочка, узелок, зарубка, камушек …

Длина записи при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков.

Сами того не осознавая, этим кодом пользуются малыши, показывая на пальцах свой возраст. Именно унарная система счисления до сих пор вводит детей в мир счета.

У разных народов существовали разные системы счисления:

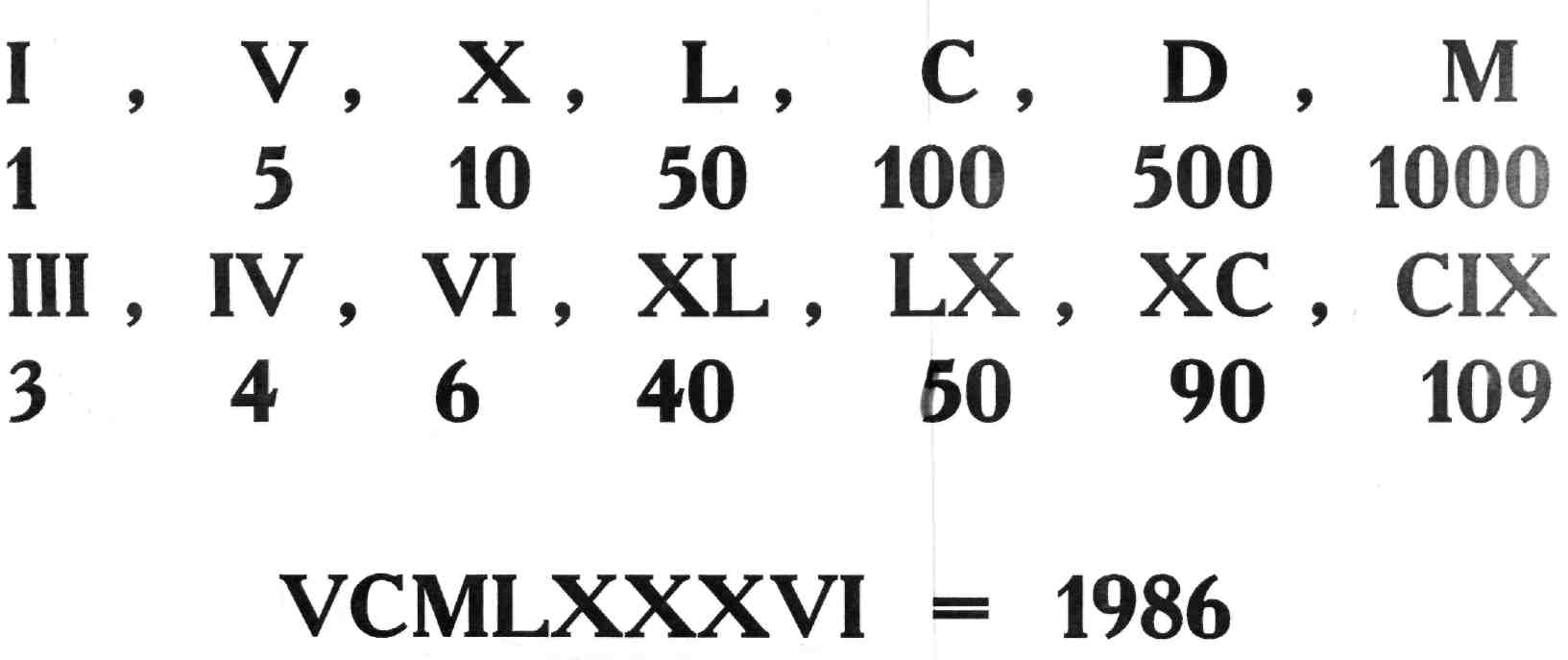► До наших дней сохранилась римская система счисления. В римской системе счисления цифры обозначаются буквами латинского алфавита (рис.1).

Для записи промежуточных чисел используется правило:

Источник

2009 год. Системой счисления называется способ представления числа символами некоторого алфавита, которые называются цифрами.Все системы счисления делятся. — презентация

Презентация была опубликована 8 лет назад пользователемЛюдмила Карпикова

Похожие презентации

Презентация на тему: » 2009 год. Системой счисления называется способ представления числа символами некоторого алфавита, которые называются цифрами.Все системы счисления делятся.» — Транскрипт:

4 Системой счисления называется способ представления числа символами некоторого алфавита, которые называются цифрами.Все системы счисления делятся на две группы:позиционные системы и непозиционные. Позиционные системы счисления характеризуются определенным алфавитом цифр и основанием.Наиболее распространенными позиционными системами счисления являются десятичная,двоичная и шестнадцатеричная. Система счисленияОснованиеАлфавит цифр Позиционные Непозиционные Десятичная Восьмеричная Шестнадцатеричная Римская ,1,2,3,4,5,6,7,8,9 Двоичная20,1 0,1,2,3,4,5,6,7 0,1,2,3,4,5,6,7,8,9,А,В,С,D, E,F 1(1),V(5),X(10),L(50),C(100) D(500),M(1000)

5 Кстати, первая позиционная система счисления была придумана еще в Древнем Вавилоне.,причем вавилонская нумерация была не десятичной,а шестидесятеричной,т.е в ней использовалось шестьдесят цифр!Интересно,что до сих пор при измерении времени мы используем основание равное 60(в 1 минуте 60 секунд,а в 1 часе-60 минут). В позиционных системах счисления величина,обозначаемая цифрой,зависит от позиции цифры в числе.Разряд числа возрастает от младших разрядов к старшим справа налево. Рассмотрим пример: десятичное число 555.Цифра 5 встречается трижды,причем самая правая обозначает пять единиц,вторая справа-пять десятков и,наконец,третья-пять сотен.Такая запись числа является записью в сокращенной форме.В полной форме запись должна выглядеть так: = 5* * *10 0 Как видно из примера,число в позиционных системах счисления записывается в виде суммы ряда степеней основания(в данном случае 10) с коэффициентами,в качестве которых выступают цифры данной системы счисления.

6 В двоичной системе основание равно 2,а алфавит цифр включает два числа 0 и 2.Следовательно число в двоичной системе счисления в полной форме записываются в виде суммы ряда степеней основания 2 с коэффициентами,в качестве которых выступают цифры 0 или 1. Сравним двоичную и десятичную системы счисления.Обе системы позиционные,т.е «вес» цифры в числе зависит от ее позиции,однако они различаются набором используемых цифр и основанием.Основание в системе счисления определяет перенос в старший разряд числа.Чем меньше основание,тем быстрее растет разрядность числа. Например, число 5 в двоичной системе в полной форме записывается следующим образом: 5=1* * *2 0 В сокращенной и более привычной форме число 5 в двоичной системе записывается так: 5=101 2

7 В непозиционных системах счисления,самой распространенной из которых является римская,значение цифры не зависит от ее положения в числе. Например, в числе ХХХ(30) цифра Х встречается трижды и,в каждом случае,обозначает одну и ту же величину-число 10, три раза по 10 в сумме дают 30. Величина числа в непозиционных системах счисления определяется как сумма или разность цифр в числе.Если меньшая цифра стоит слева от большей,то она вычитается,если справа-прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом: МСМХСV111= ( ) + (100-10)

8 Преобразование чисел из двоичной,восьмеричной и шестнадцатеричной систем счисления в десятичную выполнить довольно легко.Для этого необходимо записать число в полной форме и вычислить его значение. Например, возьмем двоичное число Запишем его в полной форме и произведем вычисления: =1* * * *2 0 =1*8 + 0*4 + 1*2 + 1*1 = Возьмем любое восьмеричное число,например Запишем его в полной форме и произведем вычисления: Возьмем любое шестнадцатеричное число,например 19F 16.Запишем его в полной форме и произведем вычисления: = 6* * *8 0 = 6*64 + 7*8 + 5*1 = F 16 = 1* * F*8 0 = 1* * *1 =

9 Перевод чисел из десятичной системы в двоичную,восьмеричную и шестнадцатеричную более сложен. Исходное десятичное число многократно(до тех пор,пока Рассмотрим алгоритм перевода числа из десятичной системы в двоичную. частное не станет равным нулю)делится на основание двоичной системы,т.е на 2.Если при делении образуется остаток,то в соответствующей двоичный разряд записывается 1,если делится без остатка,то записывается 0.Запись остатков в двоичное число ведется слева направо,т.е от младшего разряда к старшим. Двоичная Восьмеричная Шестнадцатеричная

10 1) Чем отличаются позиционные системы счисления от непозиционных? 2) Запишите двоичное число в полной форме. 3) Запишите число 1999 в римской системе счисления. 4)Переведите в десятичную систему следующие числа: Двоичные: 101 2,110 2,111 2 Восьмеричные:9 8,11 8,22 8 Шестнадцатеричный:1А 16,BF 16,9C 16 5) Переведите из десятичной системы в двоичную следующие числа: 7,9,13. Завершить показ

Источник

Кодирование числовой информации

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит системы счисления состоит из символов, которые называются цифрами.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные. В позиционных системах счисления количественное значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Непозиционные системы счисления. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков: зарубок, черточек, точек.

Такая система записи чисел называется единичной, так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Единичной системой счисления пользуются малыши, показывая на пальцах свой возраст или используя для этого счетные палочки.

Примером непозиционной системы, которая сохранилась до наших дней, может служить римская система счисления, которая начала применяться более двух с половиной тысяч лет назад в Древнем Риме. В основе римской системы счисления лежат знаки I (один палец) для числа 1, V (раскрытая ладонь) для числа 5, X (две сложенные ладони) для числа 10, а для обозначения чисел 100, 500 и 1000 используются латинские буквы С, D и М.

В римской системе счисления количественное значение цифры не зависит от ее положения в числе. Например, в римском числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три раза по 10 в сумме дают 30.

Чтобы записать число в римской системе счисления, необходимо разложить его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом:

XXVIII =10 + 10 + 5 + 1 + 1 + 1 (два десятка, пяток, три единицы).

При записи чисел в римской системе счисления применяется правило: каждый меньший знак, поставленный слева от большего, вычитается из него, в остальных случаях знаки складываются. Например, римское число IX обозначает 9 (-1 + 10), а XI обозначает 11 (10 + 1). Число 99 имеет следующее представление в римской системе счисления: XCIX = -10 + 100 — 1 + 10.

Позиционные системы счисления. Каждая позиционная система счисления имеет определенный алфавит цифр и основание. Основание системы равно количеству цифр (знаков) в ее алфавите.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе. Позиция цифры в числе называется разрядом. Разряды числа возрастают справа налево, от младших разрядов к старшим, причем значения одинаковых цифр, стоящих в соседних разрядах числа, различаются на величину основания.

В настоящее время наиболее распространенными позиционными системами счисления являются десятичная и двоичная. Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских цифр <0, 1, 2, 3, 4, 5, 6, 7, 8, 9>. Алфавит двоичной системы — две цифры <0, 1>(табл. 4.1).

Источник

СЧИСЛЕНИЕ (нумерация), способ выражения и обозначения чисел. Система счисления это знаковая система, в которой числа записываются по определенным правилам. — презентация

Презентация была опубликована 9 лет назад пользователемval22.narod.ru

Похожие презентации

Презентация на тему: » СЧИСЛЕНИЕ (нумерация), способ выражения и обозначения чисел. Система счисления это знаковая система, в которой числа записываются по определенным правилам.» — Транскрипт:

2 СЧИСЛЕНИЕ (нумерация), способ выражения и обозначения чисел. Система счисления это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами. Система счисления это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

3 Системы счисления позиционные непозиционные

4 Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Как только люди начали считать, у них появилась потребность в записи чисел. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, сколько полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету. Отголоски единичной системы счисления встречаются и сегодня. Так, чтобы узнать, на каком курсе учится курсант военного училища, нужно сосчитать, сколько полосок нашито на его рукаве. Сами того не осознавая, единичной системой счисления пользуются малыши, показывая на пальцах свой возраст, а счетные палочки используется для обучения учеников 1-го класса счету.

5 наиболее известным примером является система римских цифр. Система римских цифр основана на употреблении особых знаков для десятичных разрядов (I=1, X=10, C=100, M=1000) и их половин (V=5, L=50, D=500). Система римских цифр основана на употреблении особых знаков для десятичных разрядов (I=1, X=10, C=100, M=1000) и их половин (V=5, L=50, D=500). При этом если большая цифра стоит перед меньшей, то они складываются, а если меньшая перед большей, то меньшая вычитается из большей. При этом если большая цифра стоит перед меньшей, то они складываются, а если меньшая перед большей, то меньшая вычитается из большей. Например, IX обозначает 9, Например, IX обозначает 9, XI обозначает 11. Непозиционная система счисления

6 Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Чтобы записать число, римляне разлагали его на сумму тысяч, полутысяч, сотен, полусотен, десятков, пятков, единиц. Например, десятичное число 28 представляется следующим образом: Например, десятичное число 28 представляется следующим образом:XXVIII= (три десятка, пяток, три единицы). (три десятка, пяток, три единицы). а десятичное число 99 имеет вот такое представление: а десятичное число 99 имеет вот такое представление:XCIХ=

7 Римская непозиционная система счисления. MCMXCVIII ( )+ ( )

8 «позиционная система счисления», основанная на принципе позиционного, или поместного, значения цифр, т. е. на том, что основанная на принципе позиционного, или поместного, значения цифр, т. е. на том, что одна и та же цифра получает различные числовые значения в зависимости от ее места в записи чисел. одна и та же цифра получает различные числовые значения в зависимости от ее места в записи чисел.

9 В др. Вавилоне была распространена шестидесятеричная система и от нее человечество унаследовало час, состоящий из 60 минут по 60 секунд каждая, а также разделение круга на 360 градусов. В др. Вавилоне была распространена шестидесятеричная система и от нее человечество унаследовало час, состоящий из 60 минут по 60 секунд каждая, а также разделение круга на 360 градусов. позиционная система счисления

10 В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа. В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.

11 Наиболее употребительная система счисления десятичная, Наиболее употребительная система счисления десятичная, с цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Происхождение десятичной системы счисления связано с пальцевым счетом. с цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Происхождение десятичной системы счисления связано с пальцевым счетом. позиционная система счисления

12 777 семь единиц семь единиц семь десятков семь сотен

13 777 — это свёрнутая форма записи числа. Развёрнутая форма записи числа:

14 Пример: 4718,63 — свёрнутая форма Десятичное число 4718,63 в развернутой форме запишется так:

16 Алфавит: 0, 1 — это свёрнутая форма записи числа. Развёрнутая форма записи числа: Двоичная система счисления. В двоичной системе счисления основание 2.

18 Восьмеричная система счисления. Основание: 8 Алфавит: 0, 1, 2, 3, 4, 5, 6 и 7. Запишем восьмеричное число А 8 =7764,1 в развернутом виде:

19 Таким образом, запись 3АF16 означает: Таким образом, запись 3АF16 означает: Шестнадцатеричная система счисления. Основание: 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F.

20 2.18. Заполните все ячейки таблицы: Заполните все ячейки таблицы: Система счисленияОснованиеБазис шестнадцатеричная16 десятичная 0,1,2,3,4,5,6,7,8,9 80,1,2,3,4,5,6,7 2 Система счисления ОснованиеРазряды (степени) десятичная восьмеричная8 двоичная2

21 Д/з: § Д/з: § Задания для самостоятельного выполнения 4.1 – 4.5 Задания для самостоятельного выполнения 4.1 – 4.5

22 1.Для чего используются системы счисления? 2. Чем отличаются позиционные системы счисления от непозиционных? 3. Каково основание десятичной системы счисления, двоичной, восьмеричной и шестнадцатеричной? 4. Какие цифры входят в алфавит десятичной системы счисления, двоичной, восьмеричной и шестнадцатеричной? 5. На какую величину в позиционных системах счисления различаются одинаковые цифры, стоящие в соседних разрядах числа? 6. Сравните числа VVV и Может ли в качестве цифры использоваться символ буквы? Назовите Римские цифры.

23 I=10 X=10 C=100 M=1000 V=5 L=50 D=500

24 Какой числовой эквивалент имеет цифра 6 в числах: Какие числа записаны римскими цифрами: а) MCMXCIX; б) CMLXXXVIII; в) MCXLVII?MCMXCIXCMLXXXVIIIMCXLVII? Запишите в развернутой форме числа: А 8 = ; А 2 =101001; А 16 = ; А 8 = А 2 =101001А 16 = А 10 = 143,511; А 8 =0,134512;А 10 = 143,511А 8 =0, А 16 = 1В3,5С2.

25 I=10 X=10 C=100 M=1000 V=5 L=50 D= ( )+ ( )+(10-1) 1999 MCMXCIX

26 ( ) I=10 X=10 C=100 M=1000 V=5 L=50 D=500 CMLXXXVIII

27 (50-10) I=10 X=10 C=100 M=1000 V=5 L=50 D=500 MCXLVII

34 Правильно ли записаны числа в соответствующих системах счисления: а) А10=А,234;б) А8=-5678;в) А16=456,46; д) А2=22,2; 2. Запишите в свернутой форме следующие числа: а) А16=А*161+1*160+7*16-1+5*16-2;б) А10= 9*101+1*100+5*10-1+3* Запишите в развернутом виде числа: а) А8=143511;г) А10=143,511;б) А2=100111;в) А16=143511;д) А8=0,143511;е) А16=1A3,5C1.

Похожие презентации

4.1. Кодирование числовой информации 4.1.1. Представление числовой информации с помощью систем счисления Для записи информации о количестве объектов используются.

Системы счисления. Содержание Введение Непозиционные системы счисления Непозиционные системы счисления Единичная Римская Позиционные системы счисления.

Системы счисления Содержание : Системы счисления это. Системы счисления это. Системы счисления это. Системы счисления это. Виды систем счисления.

Кодирование числовой информации. Для записи информации о количестве объектов используются числа. Система счисления – это знаковая система, в которой числа.

Автор: Пророченко Ю.М.. Система счисления это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита,

Системы счисления. Содержание Введение Непозиционные системы счисления Непозиционные системы счисления Единичная Римская Позиционные системы счисления.

Кодирование числовой информации Системы счисления.

СИСТЕМЫ СЧИСЛЕНИЯ Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита,

Системы счисления. Все есть число», говорили пифагорийцы, подчеркивая необычайно важную роль чисел в практической деятельности. Известно множество способов.

СИСТЕМЫ СЧИСЛЕНИЯ Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита,

Система счисления – это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Представление числовой информации с помощью систем счисления.

2009 год. Системой счисления называется способ представления числа символами некоторого алфавита, которые называются цифрами.Все системы счисления делятся.

«Все есть число», говорили пифагорийцы, подчеркивая необычайно важную роль чисел в практической деятельности. Для представления чисел используются системы.

Системы счисления. 4IV IIII Система счисления – способ представления чисел и соответствующие ему правила действия над числами.

КОДИРОВАНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ. КОДИРОВАНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ.

Представление числовой информации с помощью систем счисления Урок информатики в 8 классе Разработан учителем информатики МОУ «Парбигская сош» Слепченко.

1. Виды систем счисления 2. История непозиционных систем счисления 3. Перевод чисел из десятичной СС в двоичную и обратно 4. Самостоятельная работа.

Системы счисления Почему люди разных стран говорят на разных языках, а считают одинаково?

Ефимова Е.Н.школа 8401 Системы счисления Понятие о системах счисления. Исторические сведения. Урок 1.

Источник