Построение угла между двумя плоскостями
Мерой угла между плоскостями является острый угол, образованный двумя прямыми, лежащими в этих плоскостях и проведенными перпендикулярно линии их пересечения.
- Из произвольной точки K проводят перпендикуляры к каждой из заданных плоскостей.
- Способом вращения вокруг линии уровня определяют величину угла γ° с вершиной в точке K.
- Вычисляют угол между плоскостями ϕ° = 180 – γ° при условии, что γ° > 90°. Если γ° Решение
- В произвольном месте чертежа отмечаем точку K. Из неё опускаем перпендикуляры m и n соответственно к плоскостям α и β. Направление проекций m и n следующее: m»⊥f0α, m’⊥h0α, n»⊥f0β, n’⊥h0β.
- Определяем действительный размер ∠γ° между прямыми m и n. Для этого вокруг фронтали f поворачиваем плоскость угла с вершиной K в положение, параллельное фронтальной плоскости проекции. Радиус поворота R точки K равен величине гипотенузы прямоугольного треугольника O»K»K0, катет которого K»K0 = yK – yO.
- Искомый угол ϕ° = ∠γ°, поскольку ∠γ° острый.
На рисунке ниже показано решение задачи, в которой требуется найти угол γ° между плоскостями α и β, заданными параллельными и пересекающимися прямыми соответственно.
- Определяем направление проекций горизонталей h1, h2 и фронталей f1, f2, принадлежащих плоскостям α и β, в порядке, указанном стрелками. Из произвольной точки K на пл. α и β опускаем перпендикуляры e и k. При этом e»⊥f»1, e’⊥h’1 и k»⊥f»2, k’⊥h’2.
- Определяем ∠γ° между прямыми e и k. Для этого проводим горизонталь h3 и вокруг неё поворачиваем точку K в положение K1 , при котором △CKD станет параллелен горизонтальной плоскости и отразится на ней в натуральную величину – △C’K’1D’. Проекция центра поворота O’ находится на проведенном к h’3 перпендикуляре K’O’. Радиус R определяется из прямоугольного треугольника O’K’K0, у которого сторона K’K0 = ZO – ZK.
- Значение искомого ∠ϕ° = ∠γ°, так как угол γ° острый.
Источник
Угол между плоскостями. Метод координат. Задание 14
Угол между плоскостями. Метод координант.
В этой статье я расскажу, как решать задачи на нахождение угла между плоскостями с помощью метода координат.
Сначала немного теории.
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величина двугранного угла измеряется величиной соответствующего линейного угла.
Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:
Пусть наши плоскости 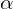

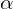

Косинус угла 
В ответе мы записываем 
Решим задачу, которая была предложена на пробнике для подготовке к ЕГЭ 17 марта 2012 года.
В правильной четырехугольной призме 
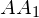





Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат:
Теперь перед нами стоит задача написать уравнения плоскости 
Подробный алгоритм нахождения уравнения плоскости 
После того, как мы найдем коэффициенты в уравнениях плоскости 

Предлагаю вам посмотреть подробное видеорешение этой задачи:
Источник
Угол между двумя пересекающимися плоскостями: определение, примеры нахождения
Статья рассказывает о нахождении угла между плоскостями. После приведения определения зададим графическую иллюстрацию, рассмотрим подробный способ нахождения методом координат. Получим формулу для пересекающихся плоскостей, в которую входят координаты нормальных векторов.
Угол между плоскостями – определение
В материале будут использованы данные и понятия, которые ранее были изучены в статьях про плоскость и прямую в пространстве. Для начала необходимо перейти к рассуждениям, позволяющим иметь определенный подход к определению угла между двумя пересекающимися плоскостями.
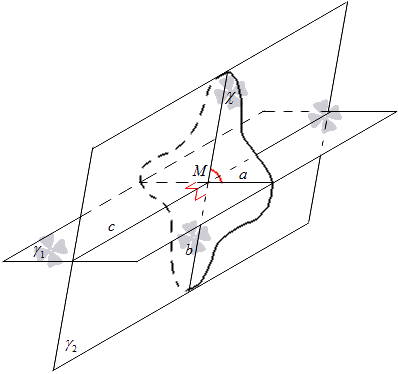
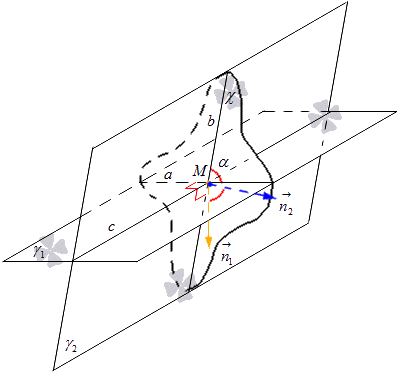
Заданы две пересекающиеся плоскости γ 1 и γ 2 . Их пересечение примет обозначение c . Построение плоскости χ связано с пересечением этих плоскостей. Плоскость χ проходит через точку М в качестве прямой c . Будет производиться пересечение плоскостей γ 1 и γ 2 с помощью плоскости χ . Принимаем обозначения прямой, пересекающей γ 1 и χ за прямую a , а пересекающую γ 2 и χ за прямую b . Получаем, что пересечение прямых a и b дает точку M .
Расположение точки M не влияет на угол между пересекающимися прямыми a и b , а точка M располагается на прямой c , через которую проходит плоскость χ .
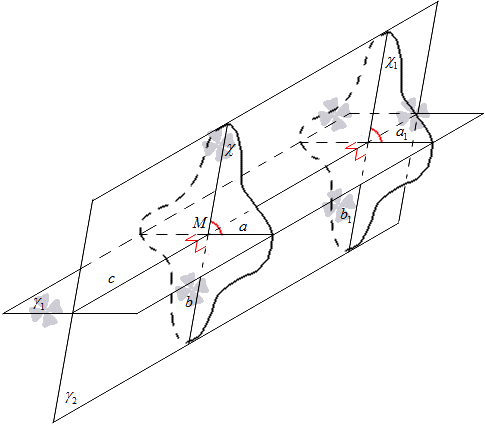
Необходимо построить плоскость χ 1 с перпендикулярностью к прямой c и отличную от плоскости χ . Пересечение плоскостей γ 1 и γ 2 с помощью χ 1 примет обозначение прямых а 1 и b 1 .
Видно, что при построении χ и χ 1 прямые a и b перпендикулярны прямой c , тогда и а 1 , b 1 располагаются перпендикулярно прямой c . Нахождение прямых a и а 1 в плоскости γ 1 с перпендикулярностью к прямой c , тогда их можно считать параллельными. Таки же образом расположение b и b 1 в плоскости γ 2 с перпендикулярностью прямой c говорит об их параллельности. Значит, необходимо сделать параллельный перенос плоскости χ 1 на χ , где получим две совпадающие прямые a и а 1 , b и b 1 . Получаем, что угол между пересекающимися прямыми a и b 1 равен углу пересекающихся прямых a и b .
Рассмотрим не рисунке, приведенном ниже.
Данное суждение доказывается тем, что между пересекающимися прямыми a и b имеется угол, который не зависит от расположения точки M , то есть точки пересечения. Эти прямые располагаются в плоскостях γ 1 и γ 2 . Фактически, получившийся угол можно считать углом между двумя пересекающимися плоскостями.
Перейдем к определению угла между имеющимися пересекающимися плоскостями γ 1 и γ 2 .
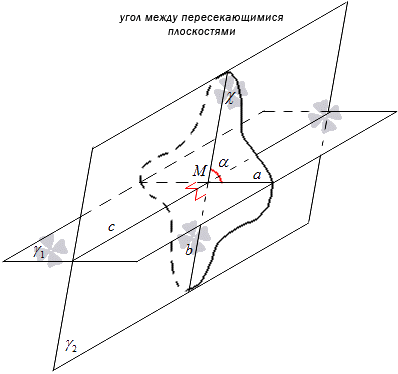
Углом между двумя пересекающимися плоскостями γ 1 и γ 2 называют угол, образовавшийся путем пересечения прямых a и b , где плоскости γ 1 и γ 2 имеют пересечение с плоскостью χ , перпендикулярной прямой c .
Рассмотрим рисунок, приведенный ниже.
Определение может быть подано в другой форме. При пересечении плоскостей γ 1 и γ 2 , где c – прямая, на которой они пересеклись, отметить точку M , через которую провести прямые a и b , перпендикулярные прямой c и лежащие в плоскостях γ 1 и γ 2 , тогда угол между прямыми a и b будет являться углом между плоскостями. Практически это применимо для построения угла между плоскостями.
При пересечении образуется угол, который по значению меньше 90 градусов, то есть градусная мера угла действительна на промежутке такого вида ( 0 , 90 ] . Одновременно данные плоскости называют перпендикулярными в случае, если при пересечении образуется прямой угол. Угол между параллельными плоскостями считается равным нулю.
Нахождение угла между двумя пересекающимися плоскостями
Обычный способ для нахождения угла между пересекающимися плоскостями – это выполнение дополнительных построений. Это способствует определять его с точностью, причем делать это можно с помощью признаков равенства или подобия треугольника, синусов, косинусов угла.
Рассмотрим решение задач на примере из задач ЕГЭ блока C 2 .
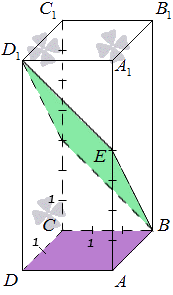
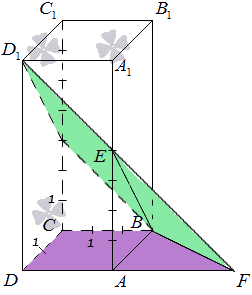
Задан прямоугольный параллелепипед А В С D A 1 B 1 C 1 D 1 , где сторона А В = 2 , A D = 3 , А А 1 = 7 , точка E разделяет сторону А А 1 в отношении 4 : 3 . Найти угол между плоскостями А В С и В E D 1 .
Для наглядности необходимо выполнить чертеж. Получим, что
Наглядное представление необходимо для того, чтобы было удобней работать с углом между плоскостями.
Производим определение прямой линии, по которой происходит пересечение плоскостей А В С и В E D 1 . Точка B является общей точкой. Следует найти еще одну общую точку пересечения. Рассмотрим прямые D A и D 1 E , которые располагаются в одной плоскости A D D 1 . Их расположение не говорит о параллельности, значит, они имеют общую точку пересечения.
Однако, прямая D A расположена в плоскости А В С , а D 1 E в B E D 1 . Отсюда получаем, что прямые D A и D 1 E имеют общую точку пересечения, которая является общей и для плоскостей А В С и B E D 1 . Обозначает точку пересечения прямых D A и D 1 E буквой F . Отсюда получаем, что B F является прямой, по которой пересекаются плоскости А В С и В E D 1 .
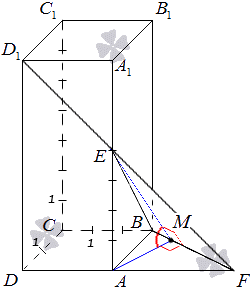
Рассмотрим на рисунке, приведенном ниже.
Для получения ответа необходимо произвести построение прямых, расположенных в плоскостях А В С и В E D 1 с прохождением через точку, находящуюся на прямой B F и перпендикулярной ей. Тогда получившийся угол между этими прямыми считается искомым углом между плоскостями А В С и В E D 1 .
Отсюда видно, что точка A – проекция точки E на плоскость А В С . Необходимо провести прямую, пересекающую под прямым углом прямую B F в точке М . Видно, что прямая А М – проекция прямой Е М на плоскость А В С , исходя из теоремы о тех перпендикулярах A M ⊥ B F . Рассмотрим рисунок, изображенный ниже.
∠ A M E — это искомый угол, образованный плоскостями А В С и В E D 1 . Из получившегося треугольника А Е М можем найти синус, косинус или тангенс угла, после чего и сам угол, только при известных двух сторонах его. По условию имеем, что длина А Е находится таким образом: прямая А А 1 разделена точкой E в отношении 4 : 3 , то означает полную длину прямой – 7 частей, тогда А Е = 4 частям. Находим А М .
Необходимо рассмотреть прямоугольный треугольник А В F . Имеем прямой угол A с высотой А М . Из условия А В = 2 , тогда можем найти длину A F по подобию треугольников D D 1 F и A E F . Получаем, что A E D D 1 = A F D F ⇔ A E D D 1 = A F D A + A F ⇒ 4 7 = A F 3 + A F ⇔ A F = 4
Необходимо найти длину стороны B F из треугольника A B F , используя теорему Пифагора. Получаем, что B F = A B 2 + A F 2 = 2 2 + 4 2 = 2 5 . Длина стороны А М находится через площадь треугольника A B F . Имеем, что площадь может равняться как S A B C = 1 2 · A B · A F , так и S A B C = 1 2 · B F · A M .
Получаем, что A M = A B · A F B F = 2 · 4 2 5 = 4 5 5
Тогда можем найти значение тангенса угла треугольника А Е М . Получим:
t g ∠ A M E = A E A M = 4 4 5 5 = 5
Искомый угол, получаемый пересечением плоскостей А В С и B E D 1 равняется a r c t g 5 , тогда при упрощении получим a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .
Ответ: a r c t g 5 = a r c sin 30 6 = a r c cos 6 6 .
Некоторые случаи нахождения угла между пересекающимися прямыми задаются при помощи координатной плоскости О х у z и методом координат. Рассмотрим подробней.
Если дана задача, где необходимо найти угол между пересекающимися плоскостями γ 1 и γ 2 , искомый угол обозначим за α .
Тогда заданная система координат показывает, что имеем координаты нормальных векторов пересекающихся плоскостей γ 1 и γ 2 . Тогда обозначим, что n 1 → = n 1 x , n 1 y , n 1 z является нормальным вектором плоскости γ 1 , а n 2 → = ( n 2 x , n 2 y , n 2 z ) — для плоскости γ 2 . Рассмотрим подробное нахождение угла, расположенного между этими плоскостями по координатам векторов.
Необходимо обозначить прямую, по которой происходит пересечение плоскостей γ 1 и γ 2 буквой c . На прямой с имеем точку M , через которую проводим плоскость χ , перпендикулярную c . Плоскость χ по прямым a и b производит пересечение плоскостей γ 1 и γ 2 в точке M . из определения следует, что угол между пересекающимися плоскостями γ 1 и γ 2 равен углу пересекающихся прямых a и b , принадлежащих этим плоскостям соответственно.
В плоскости χ откладываем от точки M нормальные векторы и обозначаем их n 1 → и n 2 → . Вектор n 1 → располагается на прямой, перпендикулярной прямой a , а вектор n 2 → на прямой, перпендикулярной прямой b . Отсюда получаем, что заданная плоскость χ имеет нормальный вектор прямой a , равный n 1 → и для прямой b , равный n 2 → . Рассмотрим рисунок, приведенный ниже.
Отсюда получаем формулу, по которой можем вычислить синус угла пересекающихся прямых при помощи координат векторов. Получили, что косинусом угла между прямыми a и b то же, что и косинус между пересекающимися плоскостями γ 1 и γ 2 выводится из формулы cos α = cos n 1 → , n 2 → ^ = n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2 , где имеем, что n 1 → = ( n 1 x , n 1 y , n 1 z ) и n 2 → = ( n 2 x , n 2 y , n 2 z ) являются координатами векторов представленных плоскостей.
Вычисление угла между пересекающимися прямыми производится по формуле
α = a r c cos n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2
По условию дан параллелепипед А В С D A 1 B 1 C 1 D 1 , где А В = 2 , A D = 3 , А А 1 = 7 , а точка E разделяет сторону А А 1 4 : 3 . Найти угол между плоскостями А В С и B E D 1 .
Из условия видно, что стороны его попарно перпендикулярны. Это значит, что необходимо ввести систему координат О х у z с вершиной в точке С и координатными осями О х , О у , О z . Необходимо поставить направление по соответствующим сторонам. Рассмотрим рисунок, приведенный ниже.
Пересекающиеся плоскости А В С и B E D 1 образуют угол, который можно найти по формуле α = a r c cos n 1 x · n 2 x + n 1 y · n 2 y + n 1 z · n 2 z n 1 x 2 + n 1 y 2 + n 1 z 2 · n 2 x 2 + n 2 y 2 + n 2 z 2 , в которой n 1 → = ( n 1 x , n 1 y , n 1 z ) и n 2 → = ( n 2 x , n 2 y , n 2 z ) являются нормальными векторами этих плоскостей. Необходимо определить координаты. По рисунку видим, что координатная ось О х у совпадает в плоскостью А В С , это значит, что координаты нормального вектора k → равняются значению n 1 → = k → = ( 0 , 0 , 1 ) .
За нормальный вектор плоскости B E D 1 принимается векторное произведение B E → и B D 1 → , где их координаты находятся путем координат крайних точек В , Е , D 1 , которые определяются, исходя из условия задачи.
Получаем, что B ( 0 , 3 , 0 ) , D 1 ( 2 , 0 , 7 ) . Потому как A E E A 1 = 4 3 , из координат точек A 2 , 3 , 0 , A 1 2 , 3 , 7 найдем E 2 , 3 , 4 . Получаем, что B E → = ( 2 , 0 , 4 ) , B D 1 → = 2 , — 3 , 7 n 2 → = B E → × B D 1 = i → j → k → 2 0 4 2 — 3 7 = 12 · i → — 6 · j → — 6 · k → ⇔ n 2 → = ( 12 , — 6 , — 6 )
Необходимо произвести подстановку найденных координат в формулу вычисления угла через арккосинус. Получаем
α = a r c cos 0 · 12 + 0 · ( — 6 ) + 1 · ( — 6 ) 0 2 + 0 2 + 1 2 · 12 2 + ( — 6 ) 2 + ( — 6 ) 2 = a r c cos 6 6 6 = a r c cos 6 6
Метод координат дает аналогичный результат.
Ответ: a r c cos 6 6 .
Завершающая задача рассматривается с целью нахождения угла между пересекающимися плоскостями при имеющихся известных уравнениях плоскостей.
Вычислить синус , косинус угла и значение угла, образованного двумя пересекающимися прямыми, которые определены в системе координат О х у z и заданы уравнениями 2 x — 4 y + z + 1 = 0 и 3 y — z — 1 = 0 .
При изучении темы общего уравнения прямой вида A x + B y + C z + D = 0 выявили, что А , В , С являются коэффициентами, равными координатам нормального вектора. Значит, n 1 → = 2 , — 4 , 1 и n 2 → = 0 , 3 , — 1 являются нормальным векторами заданных прямых.
Необходимо подставить координаты нормальных векторов плоскостей в формулу вычисления искомого угла пересекающихся плоскостей. Тогда получаем, что
α = a r c cos 2 · 0 + — 4 · 3 + 1 · ( — 1 ) 2 2 + — 4 2 + 1 2 = a r c cos 13 210
Отсюда имеем, что косинус угла принимает вид cos α = 13 210 . Тогда угол пересекающихся прямых не является тупым. Подставив в тригонометрическое тождество, получаем, что значение синуса угла равняется выражению. Вычислим и получим, что
sin α = 1 — cos 2 α = 1 — 13 210 = 41 210
Ответ: sin α = 41 210 , cos α = 13 210 , α = a r c cos 13 210 = a r c sin 41 210 .
Источник