Способ построения развертки пирамиды

Способ построения развертки пирамиды

При построении развертки пирамиды применяется метод треугольника. Развертка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников – граней пирамиды и многоугольника — основания. Поэтому построение развертки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трем сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину ребер и сторон основания.

Рисунок 137. Определение истинной величины основания и ребер пирамиды

Алгоритм построения можно сформулировать следующим образом (рис. 137):

определяют натуральную величину основания пирамиды (например, методом замены плоскостей проекций);

определяют истинную величину всех ребер пирамиды любым из известных способов (в данном примере натуральная величина всех ребер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);

с троят основание пирамиды и по найденным трем сторонам строят какую-либо из боковых граней, пристраивая к ней следующие (рис.138).

Рисунок 138. Построение развертки пирамиды

Точки, расположенные внутри контура развертки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех ребер, по которым многогранник разрезан, на развертке соответствуют две точки, принадлежащие контуру развертки.

Примером первой точки на рисунках служит точка К₀ и К О SА D, а иллюстрацией второго случая являются точки М₀ и М₀ * . Для определения точки К₀ на развертке пришлось по ее ортогональным проекциям найти длины отрезков АМ ( метод замены плоскостей проекций) и SК (метод вращения). Эти отрезки были использованы затем при построении на развертке сначала прямой S₀ М₀ и, наконец, точки К₀.

Источник

Лекция 6. Многогранники

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра .
Ребра, пересекаясь, образуют вершины .
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

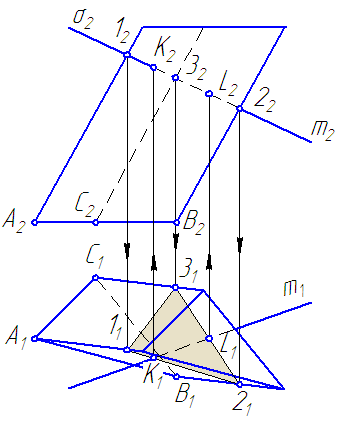
Дана пирамида, основание которой параллельно π₁. Основание представляет собой некоторый треугольник.

S – вершина пирамиды (Рисунок 6.1).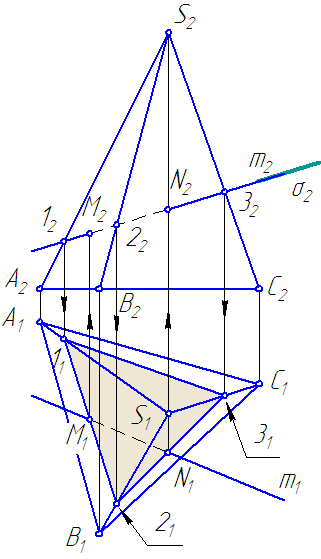

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции необходимо выполнять при помощи пропорционального деления отрезка.

1. В сечении находим точки M и N принадлежащие прямой m.
2. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

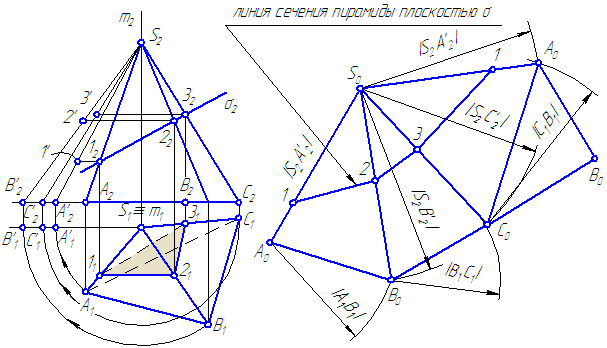
Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки \overline<1>,\overline<2>,\overline <3>, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

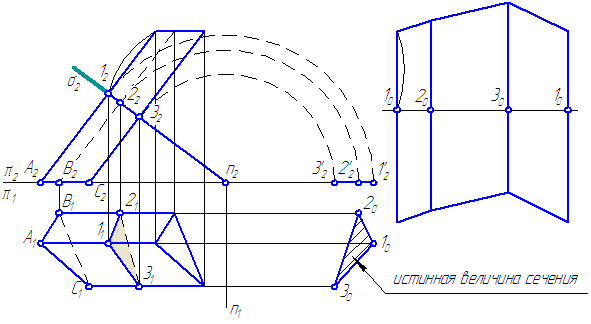
Рисунок 6.4 – Построение развёртки призмы
Порядок построения :

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

1. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

Возможны два случая пересечения многогранников (Рисунок 6.5):

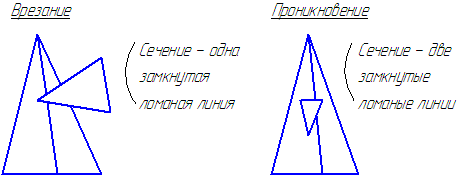
Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

Построить линии пересечения призмы с пирамидой (Рисунок 6.6).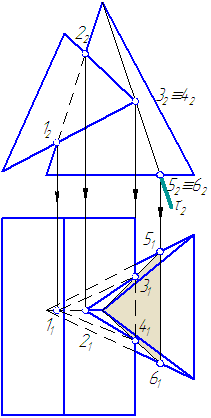

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

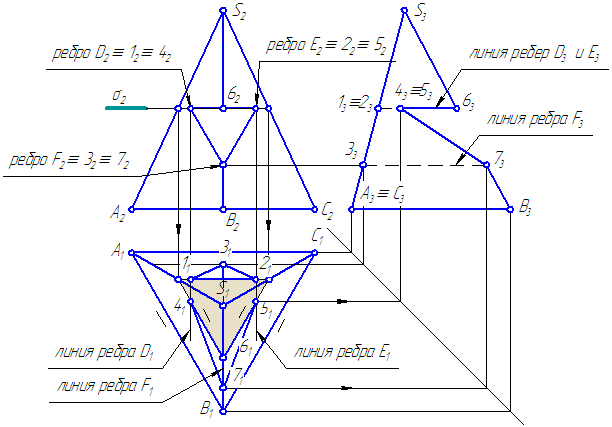
Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение :

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

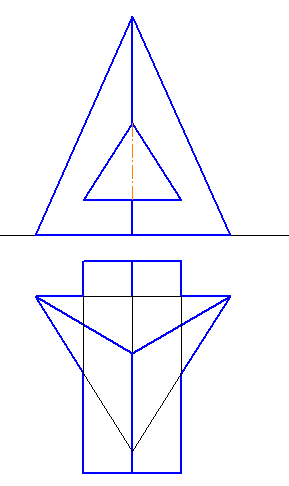
Рисунок 6.8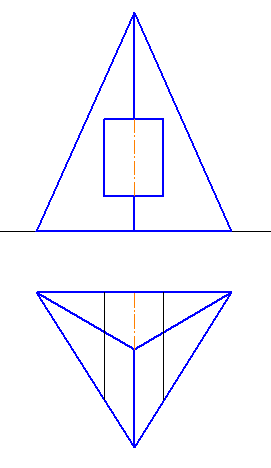

Рисунок 6.9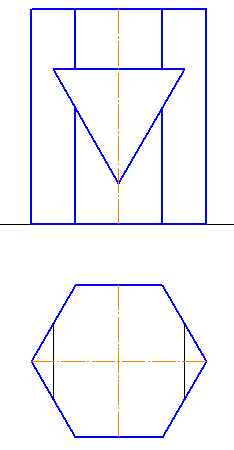

Рисунок 6.10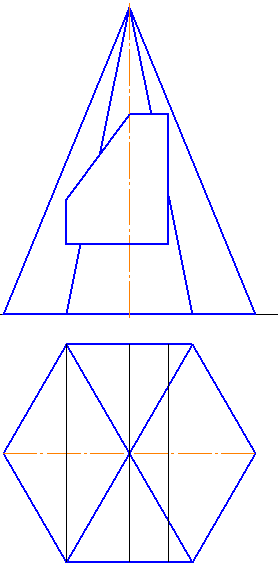

Рисунок 6.11

Источник

Построение развертки поверхности пирамиды способом треугольников

Развертка поверхности пирамиды — это плоская фигура, составленная из основания и граней пирамиды, совмещенных с некоторой плоскостью. На примере ниже мы рассмотрим построение развертки способом треугольников.

Пирамиду SABC пересекает фронтально-проецирующая плоскость α. Необходимо построить развертку поверхности SABC и нанести на нее линию пересечения.

На фронтальной проекции S»A»B»C» отмечаем точки D», E» и F», в которых след α_v пересекается с отрезками A»S», B»S» и C»S» соответственно. Определяем положение точек D’, E’, F’ и соединяем их друг с другом. Линия пересечения обозначена на рисунке красным цветом.

Определение длины ребер

Чтобы найти натуральные величины боковых ребер пирамиды, воспользуемся методом вращения вокруг проецирующей прямой. Для этого через вершину S перпендикулярно горизонтальной плоскости H проведем ось i. Поворачивая вокруг нее отрезки SA, SB и SC, переместим их в положение, параллельное фронтальной плоскости V.

Действительные величины ребер равны проекциям S»A»₁, S»₁B»₁ и S»C»₁. Отмечаем на них точки D»₁, E»₁, F»₁, как это показано стрелками на рисунке выше.

Треугольник ABC, лежащий в основании пирамиды, параллелен горизонтальной плоскости. Он отображается на ней в натуральную величину, равную ∆A’B’C’.

Порядок построения развертки

В произвольном месте на чертеже отмечаем точку S₀. Через нее проводим прямую n и откладываем отрезок S₀A₀ = S»A»₁.

Строим грань ABS = A₀B₀S₀ как треугольник по трем сторонам. Для этого из точек S₀ и A₀ проводим дуги окружностей радиусами R₁ = S»B»₁ и r₁ = A’B’ соответственно. Пересечение данных дуг определяет положение точки B₀.

Грани B₀S₀C₀ и C₀S₀A₀ строятся аналогично. Основание пирамиды в зависимости компоновки чертежа присоединяется к любой из сторон: A₀B₀, B₀C₀ или C₀A₀.

Нанесем на развертку линию, по которой плоскость α пересекается с пирамидой. Для этого на ребрах S₀A₀, S₀B₀ и S₀С₀ отметим соответственно точки D₀, E₀ и F₀. При этом точка D₀ находится на пересечении отрезка S₀A₀ с окружностью радиусом S»D»₁. Аналогично E₀ = S₀B₀ ∩ S»E»₁, F₀ = S₀C₀ ∩ S»F»₁.

Источник

Как сделать объемную пирамиду — пошаговая инструкция

Обычно дети изучают геометрические фигуры в начальных классах, при этом для закрепления материала учителя задают на дом сделать пирамиду. Без помощи родителей они, скорее всего, не справятся. Особых навыков для этого не понадобится, но перед тем, как сделать пирамиду из бумаги, придется создать развертку и продумать основные моменты по склеиванию.

Зачем использовать макет пирамиды?

Поделка считается универсальной, поскольку одинаково подходит для развития дошколят и детей из младших классов. Такое занятие развивает мелкую моторику детей, а поскольку для изготовления используется схема из бумаги, они развивают еще и образное мышление.

Когда детям удается что-то подобное сделать самостоятельно, они сохраняют поделку и оставляют ее в качестве украшения своей комнаты или рабочего пространства. Не стоит запрещать им этого, поскольку пирамида станет лишним напоминанием, что усердие дает свои результаты.

Некоторые, научившись один раз создавать фигуру с припусками, затем используют этот навык для изготовления подарочной упаковки или хранят в ней какие-то мелкие предметы. Чтобы при этом каждый раз не разбирать предмет, в нем делают небольшое отверстие, куда потом складывают пуговицы, бусины, украшения и пр.

Как сделать пирамиду из бумаги?

Заранее стоит обговорить с ребенком все основные моменты, чтобы подобрать соответствующие материалы. Перед тем, как сделать треугольник из цветного картона, определяют цель изготовления, с ребенком проговаривают, какие материалы отталкиваясь от этого лучше подобрать.

Требуемые материалы

Чтобы во время работы не отвлекаться на другие моменты, стоит заранее подготовить все требуемые инструменты. Для склеивания обычно берут ПВА или карандаш, тут отталкиваются оттого, с чем ребенок обычно работает. Помимо этого, используется бумага или картон любого оттенка формата А4, альбомный лист, ножницы, карандаш, линейка, ластик.

Если при этом используется готовый макет пирамиды, то его заранее распечатывают. При правильной подготовке ребенок не останется без работы ни на одном этапе, в этом случае он не потеряет интерес и останется доволен.

Параметры

Для получения симметричной поделки заранее определяют ее габариты. Для изготовления крупной пирамиды для каждой части используют отдельный лист, во всех остальных случаях достаточно одного листика картона или бумаги.

Пирамида из картона планируется таким образом, чтобы ее ширина равнялась длине грани квадрата. На эту часть обычно оставляют не более 15 см.

Составление чертежа

Если заранее составить развертку пирамиды, то проблем с определением параметров и симметричностью сторон не возникнет. Чертеж рисуют самостоятельно или работают с готовым шаблоном. Во время этого учитывают следующие моменты:

• В основании всегда лежит правильный многоугольник с соответствующей высотой. Размеры поделки определяют самостоятельно.
• Заранее изображаются 4 квадрата, все кроме одного при этом используются для треугольника.
• На любой боковой стороне определяют середину, от основания проводят две линии через эту точку, чтобы образовалась вершина.
• В равнобедренных треугольниках квадраты соединяют между собой с небольшим отступом.

Независимо от выбранного шаблона и типа пирамиды, во время вырезания заготовки к краям прибавляют 0,5–1 см, это упростит работу.

Сборка модели

Разберем всю последовательность действий, чтобы во время работы не возникало вопросов:

1. Определитесь с вариантом поделки.
2. Соберите требуемый материал. В нашем случае используется плотная бумага, карандаш, ножницы, ПВА.
3. На основном материале нарисуйте квадрат и поделите его на 9 частей.
4. Определите основание, а потом нарисуйте треугольник в каждом подходящем квадрате, заранее отступите немного места для припусков.
5. Вырежьте фигуру, согните ее у основания и в тех местах, где остается припуск.
6. Проклейте все отогнутые части, а затем соедините их друг с другом.

• 
• 
• 
• 

Если используется обычный серый материал (как в нашей поделке), то после склеивания и вырезания пирамида украшается. Для этого используют карандаши, фломастеры или краски.

Особенности разных моделей

Несмотря на то, что последовательность действий остается почти такой же, при изготовлении фигур другой формы приходится учитывать некоторые моменты.

Четырехугольная

Для ее изготовления используют одну из представленных схем. Проще всего распечатать понравившийся вариант или нарисовать точно такой же. В более простом шаблоне нужные части проклеиваются и поднимаются вверх, а во втором случае они изнутри сгибаются по пунктирным линиям. Зазоры там предварительно промазывают клеем. Четырехугольная пирамида выглядит более эффектно, поэтому во время конкурсов или состязаний некоторые выбирают этот вариант.

• 
• 

Египетская

Она собирается по аналогии с базовым вариантом, но для создания требуемого эффекта используется другой материал. Одноцветная бумага не подойдет, поэтому берут материал, который имитирует поверхность пирамиды. Из каждой части вырезают треугольник и квадрат (он ложится в основание). После этого проклеивают припуски и основу, чтобы все части фиксировались.

Для египетской пирамиды потребуется хороший клей, поскольку ее дно состоит из трех частей. При неаккуратной работе поделка быстро распадется.

• 
• 

Пятиугольная

Нестандартный вариант, поскольку он получается неправильной формы. Такие пирамиды редко делают, но некоторым детям они нравятся. Шаблоны для этого есть с разными типами граней.

• 
• 
• 

Шестиугольная

Сложности с ней возникают только при попытке создания собственного шаблона. Если использовать готовый материал, то сложностей не возникнет. Стоит предварительно объяснить ребенку, что именно получится из заготовки. Прилагаем два шаблона для этой поделки: первая фигура получится более вытянутой, а вторая — приплюснутой.

• 
• 

Бумажная пирамида считается простой и при этом не очень трудоемкой поделкой, но для ее изготовления все равно потребуется внимательность, усидчивость и аккуратная работа с основными инструментами.

Источник