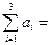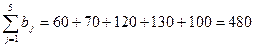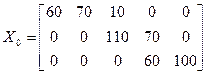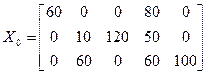Способ построения опорного плана транспортной задачи

Способ построения опорного плана транспортной задачи

Метод северо-западного угла

Пусть условия транспортной задачи заданы таблице 2.3.
Не учитывая стоимости перевозки единицы груза, начинаем удовлетворение потребностей первого потребителя B1 за счет запаса поставщика А ₁ . Для этого сравниваем a ₁ = 100 с b _i = 200, a _{1 1} меньший из объемов, т. е. = 100 ед. записываем в левый нижний угол клетки А ₁ B ₁ . Запасы первого поставщика полностью израсходованы, по этому остальные клетки первой строки прочеркиваем. Потребности В остались неудовлетворенными на 200–100=100 ед. Сравниваем этот остаток с запасами поставщика А ₂ : так как 100 ₂ .B ₁ , чем полностью удовлетворяем потребности потребителя B ₁ , а оставшиеся клетки в первом столбце прочеркиваем.

Таблица 2.3

У поставщика А ₂ осталось 150 ед. груза. Удовлетворяем потребителя B ₂ за счет оставшегося у поставщика А ₂ груза. Для этого сравниваем этот остаток с потребностями потребителя B ₂ : 150 ₂ B ₂ и, так как запасы А ₂ полностью израсходованы, прочеркиваем остальные клетки второй строки. Потребности B ₂ остались неудовлетворенными на 50 ед. Удовлетворяем их за счет поставщика А ₃ и переходим к удовлетворению B ₃ за счет остатка, имеющегося у поставщика А ₃ , и т. д. Процесс продолжаем до тех пор, пока не удовлетворим всех потребителей за счет запасов поставщиков. На этом построение первоначального опорного плана заканчивается.
Таким образом, в табл. в правых верхних углах клеток стоят числа, определяющие стоимость перевозки единицы грузов, а в левых нижних углах — числа, определяющие план перевозок, так как их сумма по строкам равна запасам соответствующего поставщика, а сумма по столбцам — потребности соответствующего потребителя.
Проверим, является ли план, построенный в табл. 2.2, опорным. Видим, что, начиная движение от занятой клетки A1B1, вернуться не только в нее, но и в любую другую занятую клетку, двигаясь только по занятым ячейкам, невозможно. Следовательно, план является опорным. В то же время план невырожденный, так как содержит точно m + n -1 = 4 + 5 — 1 = 8 занятых клеток.
При составлении первоначального опорного плана методом северо-западного угла стоимость перевозки единицы груза не учитывалась, поэтому построенный план далек от оптимального, получение которого связано с большим объемом вычислительных работ. Поэтому рассмотренный метод используется при вычислениях-с помощью ЭВМ.
Найдем общую стоимость составленного плана как сумму произведений объемов перевозок, стоящих в левом углу занятых клеток, на соответствующие стоимости в этих же ячейках:
Z = 100 *10 + 100*2 + 150 *7+ 50 *5 + 100*3 + 50*2 + 50*16+ 250*13 = 6950 (eд. стоимости)
Если при составлении опорного плана учитывать стоимость перевозки единицы груза, то, очевидно, план будет значительно ближе к оптимальному.

Метод минимальной стоимости

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a _i , или b _j . Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.
Составим с помощью этого метода опорный план уже рассмотренной задачи. Запишем ее условие в таблицу (табл. 2.5). Выбираем в таблице наименьшую стоимость (это стоимость, помещенная в клетке A ₁ , B ₄ ) так как A ₁ = b ₄ , 100 ед. груза помещаем в этой клетке и исключаем из рассмотрения первую строку и четвертый столбец. В оставшейся таблице стоимостей наименьшей является стоимость, расположенная в клетке A ₂ , B ₁ и в клетке A ₃ , B ₅ . Заполняем любую из них, например A ₂ , B ₁ . Имеем 200 ₁ . В клетку A ₃ , B ₅ записываем 200 ед. и исключаем из рассмотрения строку A ₃ . В оставшейся таблице стоимостей снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получен план
X = (X ₁₄ = 100; X ₂₁ = 200; X ₂₂ = 50; X ₃₅ = 200, X ₄₂ = 150; X ₄₃ = 100; X ₄₅ = 50),
остальные значения переменных равны нулю.

Таблица 2.5

План не содержит циклов и состоит из семи положительных перевозок, следовательно, является вырожденным опорным планом. Определим его стоимость:
Z = 100*1+200*2+50*7+200*2+150*8+100*12+50*13= 4300 (ед)
Стоимость плана перевозок значительно меньше, следовательно, он ближе к оптимальному.

Метод аппроксимации Фогеля

Данный метод состоит в следующем:

1. на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы;
2. находят max Δc _ij и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность.

Процесс продолжается до тех пор, пока все грузы не будут развезены по потребителям. Данный метод в ряде задач приводит к оптимальному плану. Решим этим методом задачу из примера 2.6.1 (см. табл.2.7).

Таблица 2.7

На первом шаге заполняем клетку A ₃ B ₁ (max Δc = 5 и min c _ij = 6), исключаем 1-ый столбец, отметив в дополнительной строке буквой «В» факт выполнения заказа пункта B ₁ . Находим новые разности минимальных тарифов по строкам (в столбцах они не изменились) и max Δc = 2 в 1-ой строке и в 4-ом столбце. Заполняем клетку A ₁ B ₄ и исключаем 4-й столбец и т.д. В конце остается последовательно заполнить клетки 3-го столбца остатками запасов в A ₁ , A ₃ , A ₂ . Составленный опорный план дает значение Z ₃ = 909 ₂ .

Метод двойного предпочтения

Если таблица стоимостей велика, то перебор всех элементов затруднителен. В этом случае используют метод двойного предпочтения, суть которого заключается в следующем.
В каждом столбце отмечают знаком V клетку с наименьшей стоимостью. Затем то же проделывают в каждой строке. В результате некоторые клетки имеют отметку VV. В них находится минимальная стоимость, как по столбцу, так и по строке. В эти клетки помещают максимально возможные объемы перевозок, каждый раз исключая из рассмотрения соответствующие столбцы или строки. Затем распределяют перевозки по ячейкам, отмеченным знаком V. В оставшейся части таблицы перевозки распределяют по наименьшей стоимости.

Источник

Построение опорного плана транспортной задачи

Его можно найти несколькими способами. Рассмотрим наиболее распространенные.

а) Метод северо-западного угла.

Он заключается в том, что в начале максимально допустимое количество груза помещается в верхнюю левую (северо-западную) клетку таблицы, затем заполняется соседняя клетка в строке или в столбце, в зависимости от того, где имеются еще неиспользованные возможности перевозок.

Таким же образом (вправо и вниз) производится распределение всего количества груза.

При таком заполнении стоимость перевозки единицы груза не учитывается.

Построить опорный план транспортной задачи для исходных данных, приведенных в таблице.

Пункты отправления	Пункты назначения	Запасы
В1	В2	В3	В4	В5
А1
А2
А3
Потребности

Определим тип задачи

следовательно, задача закрытого типа. Построим опорный план методом северо-западного угла .

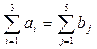
Пункты отправления	Пункты назначения	Запасы
В1	В2	В3	В4	В5
А1
А2
А3
Потребности

Таким образом , опорный план имеет вид:

Определим стоимость перевозок:

С₀=2×60+3×70+4×10+1×110+7×60+2×100=1380

б) Метод минимального элемента.

В этом случае на каждом шаге вычислений выбирают клетку с минимальным тарифом перевозок (если таких клеток несколько , то выбирают любую из них) и помещают в эту клетку максимально допустимое количество груза, с учетом имеющихся запасов и требуемых потребностей. Заполняя по этому принципу требуемое количество клеток, получим опорный план; при этом стоимость перевозок, как правило, меньше, чем в предыдущем методе.

Построить опорный план транспортной задачи для условий предыдущего примера методом минимального элемента.

Пункты отправления	Пункты назначения	Запасы
В1	В2	В3	В4	В5
А1
А2
А3
Потребности

С₀=2×60+2×80+4×10+120+4×50+7×60+2×100=1260

Источник

Решение транспортной задачи

Первым этапом решения транспортной задачи является определение ее типа (открытая или закрытая, или иначе сбалансированная или не сбалансированная). Приближенные методы (методы нахождения опорного плана) позволяют на втором этапе решения за небольшое число шагов получить допустимое, но не всегда оптимальное, решение задачи. К данной группе методов относятся методы:

• вычеркивания (метод двойного предпочтения);
• северо-западного угла;
• минимального элемента;
• аппроксимации Фогеля.

Опорное решение транспортной задачи

Приближенные методы решения транспортной задачи.
Метод вычеркивания (метод двойного предпочтения). Если в строке или столбце таблицы одна занятая клетка, то она не может входить в какой-либо цикл, так как цикл имеет две и только две клетки в каждом столбце. Следовательно, можно вычеркнуть все строки таблицы, содержащие по одной занятой клетке, затем вычеркнуть все столбцы, содержащие по одной занятой клетке, далее вернуться к строкам и продолжить вычеркивание строк и столбцов. Если в результате вычеркивания все строки и столбцы будут вычеркнуты, значит, из занятых клеток таблицы нельзя выделить часть, образующую цикл, и система соответствующих векторов условий является линейно независимой, а решение опорным. Если же после вычеркиваний останется часть клеток, то эти клетки образуют цикл, система соответствующих векторов условий линейно зависима, а решение не является опорным.
Метод «северо-западного угла» состоит в последовательном переборе строк и столбцов транспортной таблицы, начиная с левого столбца и верхней строки, и выписывании максимально возможных отгрузок в соответствующие ячейки таблицы так, чтобы не были превышены заявленные в задаче возможности поставщика или потребности потребителя. На цены доставки в этом методе не обращают внимание, поскольку предполагается дальнейшая оптимизация отгрузок.
Метод «минимального элемента». Отличаясь простотой данный метод все же эффективнее чем, к примеру, метод Северо-западного угла. Кроме того, метод минимального элемента понятен и логичен. Его суть в том, что в транспортной таблице сначала заполняются ячейки с наименьшими тарифами, а потом уже ячейки с большими тарифами. То есть мы выбираем перевозки с минимальной стоимостью доставки груза. Это очевидный и логичный ход. Правда он не всегда приводит к оптимальному плану.
Метод «аппроксимации Фогеля». При методе аппроксимации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную. В строке (или в столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.

Источник