Способ построения магических квадратов

МЕТОДЫ ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ

Уважаемые читатели! Эта страница является Приложением к главе “Магические квадраты” из книги “Компьютер решает головоломки”. Она адресована тем, кого заинтересовала тема “Магические квадраты”. Изложенные методы построения магических квадратов я нашла в литературе (в основном это журналы “Наука и жизнь”). Но! не нашла методов построения магических квадратов чётного (или: чётно-нечётного) порядка, не являющихся чётно-чётными (то есть порядок таких квадратов делится на число 2, но не делится на число 4), например, шестого, десятого и т. д. Этот метод я изобрела сама. Поэтому я пока не привожу его здесь. Делаю заявку на изобретение нового метода, которого нет в литературе! Я не могу сказать со 100% уверенностью, что в литературе вообще нет методов построения магических квадратов чётно-нечётного порядка. Надо поискать получше. Но даже если они и есть, то, вполне возможно, что они отличаются от метода, придуманного мной. Приглашаю всех заинтересовавшихся рассмотреть тему подробно и сообщить мне, нашлись ли такие методы. Или мой метод пока единственный?

А теперь перехожу к методам построения магических квадратов нечётного и чётно-чётного порядка.

Магические квадраты нечётного порядка

Если магический квадрат третьего порядка нетрудно построить простым перебором всевозможных комбинаций, то, уже начиная с квадрата четвёртого порядка, дело осложняется. Вы убедились в этом, если решали задачу о магическом квадрате четвёртого порядка, приведённую в разделе 1. Математики изобрели несколько методов построения магических квадратов. Начнём с метода террас, который применяется для построения магических квадратов нечётного порядка: пятого, седьмого и т. д. Рассмотрим его на примере магического квадрата пятого порядка.

С четырёх сторон к исходному квадрату 5х5 добавляются террасы так, чтобы получился зубчатый квадрат того же порядка, что и исходный (рис. 1). В полученной фигуре располагают числа от 1 до 25 в естественном порядке косыми рядами снизу вверх (рис. 1) или сверху вниз (рис. 2). Числа в террасах, не попавшие в квадрат, перемещаются как бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным сторонам квадрата. На рис. 3 и 4 изображены готовые магические квадраты, они аналогичны по структуре, только один повёрнут на 90 градусов относительно центра квадрата. Заметим, что методом террас можно построить не только традиционный магический квадрат нечётного порядка (то есть заполненный числами от 1 до n 2 ), но и квадрат, заполненный любыми другими числами, лишь бы разность между каждым последующим и предыдущим числом была постоянной. Так, на рис. 5 вы видите нетрадиционный магический квадрат пятого порядка, заполненный чётными числами от 2 до 50, построенный методом террас. Предлагаю вам построить методом террас магические квадраты седьмого и/или девятого порядка.

Источник

Основные методы построения магических квадратов с нечетным числом клеток

Статья просмотрена: 4986 раз

Библиографическое описание:

Бурханова, Ю. Н. Основные методы построения магических квадратов с нечетным числом клеток / Ю. Н. Бурханова, Е. А. Касаткина. — Текст : непосредственный // Молодой ученый. — 2010. — № 4 (15). — С. 29-35. — URL: https://moluch.ru/archive/15/1386/ (дата обращения: 20.11.2021).

Предлагаемая вниманию читателей статья посвящена вопросу, стоящему довольно далеко от центральной линии развития математической науки.

Священные, волшебные, загадочные, таинственные совершенные… Как только их не называли. Они пользовались особой популярностью у прорицателей, астрологов и врачевателей. Привлекающие своей красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множество тайн… Знакомьтесь: магические квадраты – удивительные представители воображаемого мира чисел.

Учение о магических квадратах занимало в математике значительное место лишь в тот период времени, когда всем руководили суеверия и астрология; в дальнейшем при возникновении новых естественнонаучных и технических задач теория магических квадратов стала не нужна. Однако учение о магических квадратах до сих пор может представлять интерес для любителей математики, в первую очередь для учащихся, в силу простоты и наглядности задач, не говоря уже о том, что это учение представляет собой благодарное поле приложения ряда более теоретико-числовых концепций.

Предлагаю вниманию читателя рассмотреть наиболее известные методы построения магических квадратов с нечетным числом клеток. При этом мы ограничиваемся лишь «классическими» магическими квадратами, т.е. квадратами, состоящими из последовательных натуральных чисел от 1 до .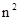

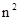
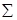
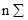
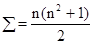
Числовым квадратом порядка n, где n – некоторое положительное целое число, мы будем называть квадрат, разбитый на n 2 клеток, в которых размещены ( в некотором порядке) целые числа от 1 до . Числовой квадрат мы будем называть магическим, если суммы, получаемые от сложения чисел каждого горизонтального ряда, каждого вертикального ряда и обеих диагоналей, одинаковы. Так как квадрат порядка n и сумма чисел каждого ряда одинакова, то сумма всех чисел, размещенных в магическом квадрате, равна . С другой стороны, она равна[3]

. (1)

Условия равенства суммы элементов отдельных строк, столбцов и диагоналей числу 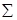мы будем называть условиями магичности этих строк, столбцов и диагоналей.[3]

Пример магического квадрата порядка 4 приведен на рис.1. (это так называемый квадрат Дюрера, изображенный на его гравюре «Меланхолия»). Для него в согласии с формулой (1), .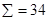

Рис.1. Квадрат Дюрера

Несмотря на то, что в свое время (особенно в XVI- XVIII веках) магические квадраты были предметом пристального изучения известных математиков, все же она не может считаться завершенной. Достаточно сказать, что до сих пор не известен никакой общий метод построения всех магических квадратов данного порядка n. Можно лишь утверждать, что это число делится на 8, так как из любого магического квадрата поворотами на 90 вокруг центра и отражениями в сторонах получаются еще 7 новых магических квадратов[4].

Клетки магического квадрата порядка n мы будем обозначать парами целых чисел (x,y) – их координатами, где х – номер вертикального ряда, у – номер горизонтального ряда, на их пересечении находится данная клетка[2]. При этом вертикальные мы нумеруем слева направо, а горизонтальные – снизу вверх. В качестве номеров мы будем использовать числа

Сдвигая основной квадрат параллельно самому себе на векторы с целочисленными координатами, делящимися на n, мы получим систему налегающих друг на друга квадратов порядка n, покрывающую всю плоскость. Две клетки, принадлежащим двум таким квадратам и занимающие относительно них одинаковое положение, мы будем называть эквивалентными. В дальнейшем эквивалентные клетки будут играть одинаковую роль и будут рассматриваться как одинаковые. Каждое целое число z=1, 2, . . ., n 2 мы можем записать в виде

где r и s – некоторые числа системы (2), однозначно определенные числом z и, обратно определяющее это число. Мы будем числа r и z называть координатами числа z[2].

Например, при n=3 координаты чисел

z=1, 2, 3, 4, 5, 6, 7, 8, 9

имеют соответственно вид

При задании некоторого магического квадрата порядка n каждой паре r,s сопоставляется пара чисел х, у – координаты клетки квадрата, в которую вписано число с координатами r, s. Другими словами, числа х и у являются функциями чисел r и s. Обозначая эти функции буквами f и g, мы получим, следовательно, что х = f(r, s) и у = g(r, s).

В дальнейшем любую пару f(r, s) и g(r, s) мы будем называть методом построения магических квадратов[2].

Описанное сведение задачи построения магического квадрата к задаче построения пары функций f(r, s) и g(r, s) позволяет, в частности, классифицировать способы построения магических квадратов в зависимости от характера этих функций.

Индийский метод составления магических квадратов (иногда называемые также сиамским) является, по-видимому, самым древним алгоритмом построения магических квадратов произвольного нечетного порядка n=2m+1. этот алгоритм описывают следующими правилами[2]:

1 . Числа от 1 до n2 поочередно вписываются в клетки основного квадрата.

2 . Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.

3 . Число 1 вписывается в среднюю клетку верхнего ряда, т.е. в клетку с координатами (m, 2m).

4 . Если число z вписано в клетку с координатами (х, у), то следующее число z+1 вписывается в клетку с координатами (х+1, у+1), т.е. в клетку, смежную с клеткой (х, у), в направлении восходящей диагонали, при условии, что эта последняя клетка еще свободна от чисел.

5 . Если клетка с координатами (х+1, у+1) уже занята некоторым числом, то число z+1 вписывается в клетку с координатами (х, у-1), т.е. в клетку, непосредственно примыкающую снизу к клетке (х, у). (оказывается это всегда возможно, т.е. клетка (х, у-1) обязательно свободна от чисел).

На рис.2 изображен магический квадрат третьего порядка, построенный индийским методом. Для ясности в этом рисунке заполнены также некоторые клетки вне основного квадрата. Не описывая подробно это построение, мы укажем лишь, что число 1 вписано на основании правила 1 и 3 , число 2 – на основании правил 4 и 2 , число 3 – на основании правил 4 и 2 , число 4 – на основании правил 5 и 2 , число 5 – на основании правила 4 , число 6 – на основании правила 4 , число 7 – на основании правил 5 и 2 , число 8 – на основании правил 4 и 2 и, наконец, число 9 – на основании правил 4 и 2 .

Источник

Магические квадраты

История открытия магических квадратов; элементарные принципы их построения. Линейный метод построения магических квадратов порядка n. Описание методов Москопула, альфила и Баше. Особенности построения магических квадратов четного и нечетного порядков.

Рубрика	Математика
Вид	курсовая работа
Язык	русский
Дата добавления	24.07.2014
Размер файла	992,4 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Размещено на http://www.allbest.ru/

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

по алгебре на тему:

§1. Элементарное построение магических квадратов при N = 3; 4

§2. Линейный алгоритм построения магических квадратов нечетного порядка

§3. Классические алгоритмы построения магических квадратов нечетного порядка

§4. Построение магических квадратов четного порядка

§5. Индуктивный метод построения магических квадратов произвольного порядка

Магический квадрат — это квадратная таблица nЧn, заполненная n 2 числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n 2 . Магический квадрат называется ассоциативным или симметричным, если сумма любых двух чисел, расположенных симметрично относительно центра квадрата, равна n 2 + 1.

Магический квадрат — древнекитайского происхождения. Согласно легенде, во времена правления императора Ю (около 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы (рис. 0.1, а), и эти знаки известны под названием ло-шу и равносильны магическому квадрату (рис. 0.1, б).

Рис. 0.1. а) таинственные иероглифы на панцире черепахи; б) магический квадрат

В XI в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера (рис. 0.2), изображенный на его знаменитой гравюре «Меланхолия I» [4].

Рис. 0.2. Магический квадрат А.Дюрера.

Дата создания гравюры (1514) указана числами, стоящими в двух центральных клетках нижней строки. Магическим квадратам приписывали различные мистические свойства. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы. Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты.

В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры [3].

§1. Элементарное построение магических квадратов при N = 3; 4

Построение магического квадрата при N = 3

Из чисел ряда подбираем группы. В каждой группе по n чисел (здесь по 3 числа). Сумма чисел каждой группы должна равняться У₀ (здесь У₀ = 15).

Готовые группы нужно так разместить в клетках квадрата, чтобы числа группы располагались прямыми рядами: по строкам, по столбцам и по диагоналям. Из 9 чисел натурального ряда можно составить только 8 групп:

1. 1 + 5 + 9 = 15 (в этой группе есть пара: 1 + 9 = у = 10)

4. 2 + 5 + 8 = 15 (2 + 8 = у)

7. 3 + 5 + 7 = 15 (3 + 7 = у)

8. 4 + 5 + 6 = 15 (4 + 6 = у)

Число 5 входит в 4 группы. Это значит, что клетка для числа 5 находится на пересечении четырех прямых рядов. В квадрате 3 Ч 3 клетки есть только одна такая клетка — средняя (рис. 1.1,а).

Рис. 1.1. а)средняя клетка; б)угловая клетка; в)средняя клетка с края

Следовательно, число 5 должно находиться только в центре квадрата и нигде более. Каждые два числа, находящиеся в одной группе и в одном ряду с числом 5, составляют пару. Эти пары располагаются симметрично по отношению к центру квадрата. Поэтому внутренняя структура будет обладать полной центральной симметрией.

Каждое четное число ряда встречается в трех группах. Это значит, что четные числа находятся на пересечении трех прямых рядов, то есть в угловых клетках (рис.1.1, б). Каждое из четырех оставшихся нечетных чисел — 1, 3, 7, 9 — входит только в 2 группы. Их место — в средних клетках по краям квадрата (рис. 1.1, в).

Если для записи единицы из четырех пригодных клеток выбрать среднюю клетку верхней строки, то для числа 9 оказывается пригодной только одна клетка — средняя на нижней строке. Теперь можно заполнить всю первую строку: 6 + 1 + 8 или 8 + 1 + 6. Это не два варианта, а только вариант и его невариант.

Числа в нижних угловых клетках определяются диагоналями:

6 + 5 + 4 и 8 + 5 + 2.

Последние два числа 7 и 3 занимают свои места так, как подсказывают группы «5» и «6» (рис. 1.2).

Рис. 1.2. Построение магического квадрата

Построение магического квадрата при N = 4

Начнём построение магических квадратов 4 Ч 4 с преобразования немагического квадрата такого же размера, заполненного числами от 1 до 16 в их естественном порядке. Задача решается (в одном только варианте), если поменять местами числа четырех пар: 2 и 15, 3 и 14, 5 и 12, 8 и 9 (рис. 1. 3).

Рис. 1.3. Построение магического квадрата. Полученный таким способом квадрат оказывается магическим, а сам способ известен ещё со времён Дюрера [1]

Линейный метод построения магических квадратов порядка n имеет вид:

Если и , то , где []- знак целой части, и (mod n).

Поэтому, формулы (1) можно записать в следующем виде:

Подставляя в равенства (2) числа , получаем координаты ряда клеток, часть из которых будет лежать вне основного квадрата. Затем в каждую клетку надо вписать соответствующее число z, заменяя одновременно клетки, лежащие вне основного квадрата, эквивалентными клетками этого квадрата. В результате получим некоторое заполнение клеток основного квадрата числами от 1 до , которое и будет магическим квадратом [2].

§3. Классические алгоритмы построения магических квадратов нечетного порядка

Индийский (сиамский) метод

Правила построения магических квадратов произвольного нечетного порядка n=2m+1:

1. Числа от 1 до поочередно вписываются в клетки основного квадрата.

2. Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.

3. Число 1 вписывается в среднюю клетку верхнего ряда.

4. Если число z вписано в клетку (x; y), то следующее число z+1 вписывается в клетку (x+1; y+1).

5. Если клетка (x+1; y+1) уже занята некоторым числом, то число z+1 вписывается в клетку (x; y-1).

Рассмотрим такой магический квадрат третьего порядка (рис.3.1). Число 1 вписано на основании правил 1 и 3, число 2- на основании правил 4 и 2, число 3- на основании правил 4 и 2, число 4- на основании правил 5 и 2, число 6- на основании правила 4, число 7- на основании правил 5 и 2, число 8-на основании правил 4 и 2, число 9- на основании правил 4 и 2.

Рис. 3.1. Построение магического квадрата индийским методом

Метод Москопула (метод коня)

Алгоритм последовательного заполнения клеток основного квадрата числами от 1 до :

1. Числа от 1 до поочередно вписываются в клетки основного квадрата.

2. Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.

3. Если n0 (mod 3), то начальная клетка, в которую вписывается число 1, выбирается произвольно; если же n?0 (mod 3), то за эту клетку принимается средняя клетка нижнего горизонтального ряда.

4. Если некоторое число z вписано в клетку (x;y), то число z+1 вписывается в клетку (x+1;y+2) при условии, что эта клетка еще свободна от чисел. магический квадрат линейный четный

5. Если клетка (x+1;y+2) уже занята некоторым числом, то число z+1вписывается в клетку (x;y+4).

Рассмотрим магический квадрат пятого порядка, построенный по данному методу (рис.3.2).

Рис. 3.2. Построение магического квадрата методом Москопула

Правила построения магического квадрата:

1. Числа от 1 до поочередно вписываются в клетки основного квадрата.

2. Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.

3. Число 1 вписывается в клетку (0;1).

4. Если число z вписано в клетку (x;y), то число z+1 вписывается в клетку (x+2;y+2)при условии, что эта клетка еще свободна от чисел.

5. Если клетка (x+2;y+2) уже занята, то число z+1 вписывается в клетку (x+1;y+3).

Пример построения магического квадрата пятого порядка (рис.3.3).

Рис. 3.3. Построение магического квадрата по методу альфила

Для построения магического квадрата следует выбрать на плоскости n соседних диагональных рядов, содержащих по n клеток и таких, что средняя клетка каждого ряда принадлежит нисходящей диагонали основного квадрата. Клетки левого верхнего ряда заполняются снизу вверх числами . Клетки p-го ряда, где , заполняются числами (p1)n+1, (p1)n+2, , pn (для n=9 рис.3.4).

Рис. 3.4. Заполнение магического квадрата по методу Баше

Заполненные таким образом клетки частью расположены внутри основного квадрата, частью- вне его, причем внешние клетки образуют по бокам основного квадрата четыре совершенно одинаковых выступа или террасы. Перенеся клетки террас в основной квадрат, заполним весь основной квадрат числами от 1 до (рис.3.5) [2].

Рис. 3.5. Магический квадрат по методу Баше

§4. Построение магических квадратов четного порядка

Алгоритм построения магического квадрата порядка n=2m:

1. Исходный квадрат делится на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате отмечаются диагональные элементы (например, символом #). Остальные элементы построчно заполняются порядковыми целыми числами в направлении слева- направо и сверху- вниз. Числа, приходящиеся на выделенные диагональные элементы должны быть пропущены (рис. 4.1).

Рис. 4.1. Построение магического квадрата 8-го порядка

2. Отмеченные на шаге 1 диагональные элементы квадрата заполняют пропущенными целыми числами в порядке возрастания в направлении справа- налево и снизу-вверх. Недиагональные элементы в каждом подквадрате должны быть отмечены (например, символом $), а числа, приходящиеся на них должны быть пропущены (рис. 4.2).

Рис. 4.2. Заполнение магического квадрата

3. Квадраты с пропусками диагональных и недиагональных элементов, полученные на шагах 1 и 2, объединяются в общий квадрат, где целочисленные элементы подавляют метки # или $ (рис. 4.3).

Рис. 4.3. Магический квадрат 8-го порядка

Константа этого магического квадрата равна 260, что подтверждается вычислением контрольных сумм элементов по строкам, столбцам и главным диагоналям [5].

§5. Индуктивный метод построения магических квадратов произвольного порядка

называют взаимно дополнительными, если их сумма равна . Число, дополнительное числу , обозначают символом . Таким образом, При n четном все числа ряда (3) располагаются на пары () взаимно дополнительных чисел. При n нечетном это верно для всех чисел ряда (3), за исключением среднего числа , которое дополнительно самому себе.

Квадрат порядка n-2, в котором размещены различные числа из ряда (3), называют обобщенным магическим квадратом, если:

1. сумма чисел каждого вертикального или горизонтального ряда, а также обеих диагоналей, равна ;

2. вместе с некоторым числом a ряда (3) в этот квадрат входит также и дополнительное число .

Увеличив все числа некоторого магического квадрата порядка n-2 на 2n-2, получаем обобщенный магический квадрат.

Такой квадрат можно получить из квадрата Дюрера (рис.5.1), оставляя неизменными числа 1,2, . 8 и увеличивая все остальные на 20(рис.5.2).

Рис. 5.1. Рис. 5.2. Магический квадрат Дюрера. Обобщенный магический квадрат

Некоторый магический квадрат К порядка n получается окаймлением обобщенного магического квадрата К’ порядка n-2, если, удаляя из квадрата К его крайние ряды, мы получим квадрат К’.

Рассмотрим такой квадрат (рис.5.3) полученный окаймлением обобщенного магического квадрата, изображенного на рисунке 5.2 [2].

Рис. 5.3. Обобщенный магический квадрат, полученный путем окаймления

№1. Построить магический квадрат 6-го порядка.

Китайский математик XIII века Ян Хуэй был знаком с треугольником Паскаля (арифметическим треугольником). Он оставил изложение методов решения уравнений 4-й и высших степеней, встречаются правила решения полного квадратного уравнения, суммирования прогрессий, приемы построения магических квадратов. Он сумел построить магический квадрат шестого порядка, причем последний оказался почти ассоциативным (в нем только две пары центрально противолежащих чисел не дают сумму 37, рис.6.1).

Рис. 6.1. Магический квадрат 6-го порядка

№2. Построить магический квадрат 7-го порядка.

1. Гуревич Е.Я. Тайна древнего талисмана. — М.: Наука, 1969. —150 с.

2. Постников М.М. Магические квадраты. — М.: Наука, 1964. — 84 с.

Источник