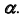- Способ построение точек пересечения прямой с плоскостью
- Порядок построения точки пересечения прямой и плоскости
- Построение точки пересечения прямой и плоскости
- Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Пересечение прямой с плоскостью в начертательной геометрии с примерами
- Пересечение проецирующей прямой с плоскостью общего положения
- Пересечение прямой общего положения с проецирующей плоскостью
- Пересечение прямой общего положения с плоскостью общего положения
Способ построение точек пересечения прямой с плоскостью

Точка пересечения прямой и плоскости
Рассмотрим пошаговую инструкцию построения точки пересечения прямой общего положения с плоскостью общего положения.Отметим, что построение точки пересечения прямой и плоскости — это одна из основ решения задач по предмету начертательная геометрия, не освоив которую дальнейшее понимание предмета будет достаточно трудным.
Порядок построения точки пересечения прямой и плоскости
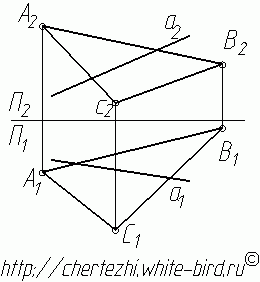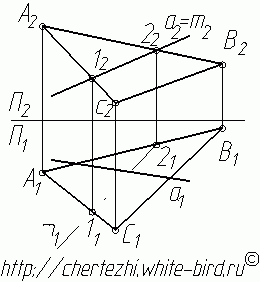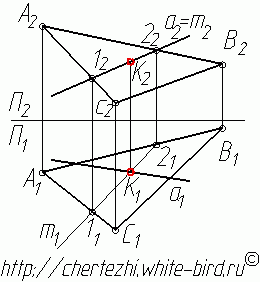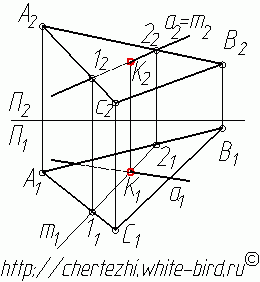
1. Заключим прямую а во вспомогательную фронтально-проецирующую плоскость (плоскость перпендикулярную фронтальной плоскости проекции). На фронтальной проекции она сольется с прямой а. Очевидно, что линия m пересечения этой плоскости с плоскостью треугольника АВС на фронтальной проекции так же будет сливаться с прямой а (а=m).
2. Определим фронтальные проекции двух точек этой линии m: точки 1 и 2.
3. Найдем их горизонтальные проекции.
4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является линией пересечения вспомогательной плоскости с плоскостью треугольника АВС, и соответственно принадлежит обеим плоскостям). Так как прямая а принадлежит вспомогательной плоскости, и прямая m принадлежит ей же, то точка пересечения этих прямых К и есть точка пересечения прямой а с плоскостью треугольника АВС.
5. С помощью линии связи найдем фронтальную проекцию точки пересечения К.
6. Осталось только определить видимость прямой а. Это можно сделать с помощью метода конкурирующих точек.
Обратите внимание, что мы начали поиск точки пересечения прямой с плоскостью с того, что заключили прямую а во вспомогательную фронтально-проецирующую плоскость. Точно таким же образом можно было заключить прямую а в горизонтально-проецирующую плоскость, и тогда бы построения начались как бы «снизу вверх», но смысл остался бы точно таким же, как и конечное решение — точка пересечения прямой с плоскостью.
Внимание! Для этой темы есть видеоурок.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
или запишите наш телефон и расскажите о нас своим друзьям — кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки — и кто-то еще сможет освоить черчение.
А вот это — не реклама. Это напоминание, что каждый из нас может сделать. Если хотите — это просьба. Мы действительно им нужны: 
Автор комментария: Дмитрий
Дата: 2012-08-16
Очень легко и понятно вы описали как найти точку пересечения прямой и плоскости, мегареспект!
Автор комментария: Алексндр
Дата: 2012-11-02
Да, теперь осилил
Автор комментария: Студент
Дата: 2012-11-14
Сделайте нормальные чертежи. Без анимации пошаговые.
Оставляйте адрес, может вам и будет подарок. Новый год ведь скоро 🙂
Автор комментария: Михаил
Дата: 2013-01-31
А вот нечего торопиться. Надо покушать как следует, сесть и всмотреться в гифку. Тогда и познаешь дзен. 🙂
Не торопиться, быть сытым и выспавшимся — да, это отличное подспорье. Спасибо за то, что указали на столь важные моменты. Да прибудет с вами сила, Михаил!
Автор комментария: Настя
Дата: 2013-03-08
Помогите пожалуста. у меня плоскость перпендикулярна фронтальной плоскости проекции и задана следами, а прямая горизонтальна горизонтальной плоскости проекций
Автор комментария: Евгений
Дата: 2014-12-21
Это простооо кул,все понятно,мегареспект вам!!
Автор комментария: Георгий
Дата: 2014-12-28
4. Соединим горизонтальные проекции точек 1 и 2 — получим горизонтальную проекцию прямой m (которая является точкой пересечения вспомогательной плоскости с плоскостью треугольника АВС. Тут надо исправить: прямая не может являться точкой. Также отсутствует закрывающая скобка.
Автор комментария: Дмитрий
Дата: 2015-05-01
Я всё равно ничего не понял. Хоть на первый взгляд это более толковое объяснение решения, чем пишут в книгах — там ваще мрак.
Автор комментария: Лиля
Дата: 2015-09-22
Высший класс! Ключевое предложение для понимания сути: «Заключим прямую а во вспомогательную фронтально-проецирующую плоскость . «
Эмм. Это сарказм? 🙂 Если да, то в свое оправдание могу сказать лишь то, что терминология должна быть вам в некоторой мере знакома. С меня лишь графический порядок решения. Но с другой стороны давать его в абсолютном отрыве от теории тоже нехорошо. Указанная в вашем комментарии фраза пригодится вам на экзамене, или как минимум на защите данной работы. Но для графического решения прямо сейчас она не так важна. Просто выполняйте по шагам.
Автор комментария: Лия
Дата: 2015-10-22
Автор комментария: Василий
Дата: 2016-10-13
Спасибо огромное.Всё доходчиво и ясно!
Автор комментария: Олег
Дата: 2016-11-17
Как быть если прямая на П2 перпендикулярна Ох, а на П1 в точку проэцируется?
Добавьте свой комментарий:
Наша страница в ВК:
чертежи Машиностроение и радио/приборостроение (специальность рк,РТ, ФАРМ и др.), строительные, 3D, печатные платы. Оформление по ескд. online. Компас, SolidWorks, P-Cad. Быстро, качественно. B96O1234@#$
Коллеги, не тратьте время. Объявления правятся быстрее, чем индексируются. Лучше предлагайте обмен ссылками, статьями. Денег в конце концов переведите — варианты всякие можно придумать.
Источник
Построение точки пересечения прямой и плоскости
Известно, что прямая пересекает плоскость, если она не принадлежит этой плоскости и не параллельна ей. Следуя приведенному ниже алгоритму, найдем точку пересечения прямой a с плоскостью общего положения α, заданной следами h0α, f0α.
- Через прямую a проводим вспомогательную фронтально-проецирующую плоскость γ. На рисунке обозначены её следы h0γ, f0γ.
- Строим проекции прямой AB, по которой пересекаются плоскости α и γ. В данной задаче точка B’ = h0α ∩ h0γ, A» = f0α ∩ f0γ. Точки A’ и B» лежат на оси x, их положение определяется по линиям связи.
- Прямые a и AB пересекаются в искомой точке K. Её горизонтальная проекция K’ = a’ ∩ A’B’. Фронтальная проекция K» лежит на прямой a».
Алгоритм решения останется тем же, если пл. α будет задана параллельными, скрещивающимися прямыми, отсеком фигуры или другими возможными способами.
Видимость прямой a относительно плоскости α. Метод конкурирующих точек
- Отметим на чертеже фронтально-конкурирующие точки A и С (рис. ниже). Будем считать, что точка A принадлежит пл. α, а С лежит на прямой a. Фронтальные проекции A» и С» совпадают, но при этом т. A и С удалены от плоскости проекций П2 на разное расстояние.
- Найдем горизонтальные проекции A’ и C’. Как видно на рисунке, точка C’ удалена от плоскости П2 на большее расстояние, чем т. A’, принадлежащая пл. α. Следовательно, участок прямой а», расположенный левее точки K», будет видимым. Участок a» правее K» является невидимым. Отмечаем его штриховой линией.
- Отметим на чертеже горизонтально-конкурирующие точки D и E. Будем считать, что точка D принадлежит пл. α, а E лежит на прямой a. Горизонтальные проекции D’ и E’ совпадают, но при этом т. D и E удалены от плоскости П1 на разное расстояние.
- Определим положение фронтальных проекций D» и E». Как видно на рисунке, точка D», находящаяся в пл. α, удалена от плоскости П1 на большее расстояние, чем т. E», принадлежащая прямой a. Следовательно, участок а’, расположенный правее точки K’, будет невидимым. Отмечаем его штриховой линией. Участок a’ левее K’ является видимым.
Источник
Пересечение прямой с плоскостью в начертательной геометрии с примерами
Содержание:
Пересечение прямой с плоскостью:
Рассмотрим три варианта, а соответственно и три алгоритма решения задачи по определению точки пересечения прямой с плоскостью:
- прямая — проецирующая, плоскость — общего положения;
- прямая — общего положения, плоскость — проецирующая;
- прямая и плоскость — общего положения.
Пересечение проецирующей прямой с плоскостью общего положения
При решении задач на определение точки пересечения проецирую- щей прямой с плоскостью общего положения используется собирательное свойство вырожденной проекции проецирующей прямой. Вырожденная проекция прямой совпадает с одноименной проекцией искомой точки. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной плоскости.
Задача:
На эпюре Монжа построить проекции точки пересечения проецирующей прямой
Алгоритм решения
- Так как прямая
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
Отметим горизонтальную проекцию
- Фронтальную проекцию
определим по принадлежности точки K плоскости
(задача 3).
Видимость прямой 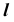
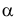
Пересечение прямой общего положения с проецирующей плоскостью
При решении задач на определение точки пересечения проецирующей плоскости с прямой общего положения используется собирательное свойство вырожденной проекции проецирующей плоскости. Одна из проекций искомой точки определяется на пересечении вырожденной проекции плоскости с одноименной проекцией заданной прямой. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной прямой.
Задача:
На эпюре Монжа построить проекции точки пересечения прямой общего положения 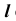
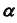
Алгоритм решения
- Так как точка K — общий элемент прямой и плоскости, а плоскость
— фронтально- проецирующая, следовательно, проекция
определится на пересечении фронтальных проекций прямой и плоскости
- Горизонтальную проекцию
определим по принадлежности точки K прямой
(задача 1).
Видимость прямой 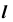
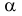
Пересечение прямой общего положения с плоскостью общего положения
Для построения точки пересечения прямой общего положения 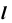
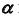
1. Заключим прямую 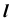
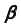
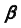
2. Строим линию пересечения заданной плоскости 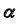
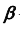
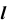
Так как линия m принадлежит заданной плоскости 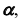
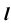
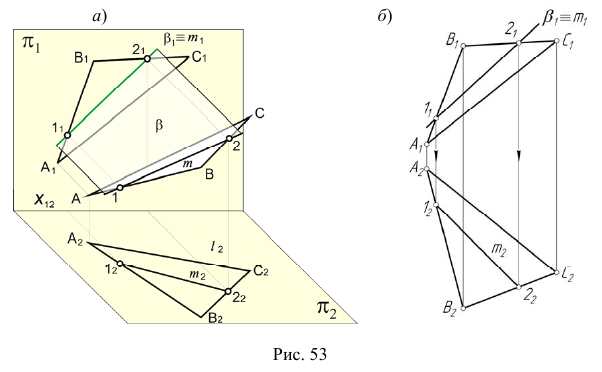
Перед решением задачи по определению точки пересечения прямой общего положения с плоскостью общего положения рассмотрим отдельно реализацию на эпюре Монжа п. 2 — построение линии пересечения проецирующей плоскости с плоскостью общего положения рис. 53, а.
Задача:
На эпюре Монжа построить проекции линии пересечения плоскости общего положения 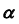
При решении этой задачи используем собирательное свойство вырожденной проекции проецирующей плоскости.
Алгоритм решения
- Определим фронтальную проекцию линии m. Так как плоскость
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
(рис. 53, б).
- Горизонтальную проекцию линии m построим, учитывая ее принадлежность плоскости
(задача 2).
- Заказать чертежи
Задача:
На эпюре Монжа построить проекции точки пересечения прямой общего положения l с плоскостью общего положения (ABC) (рис. 54, а).
Алгоритм решения
1. Заключим прямую линию l во вспомогательную проецирующую плоскость 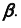
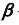
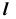
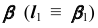
2. Построим проекции линии пересечения m заданной плоскости 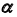
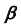
3. Определим проекции точки пересечения K прямой линии 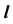
- отметим проекцию
- на пересечении
и линии проекционной связи отметим проекцию
(рис. 55, б).
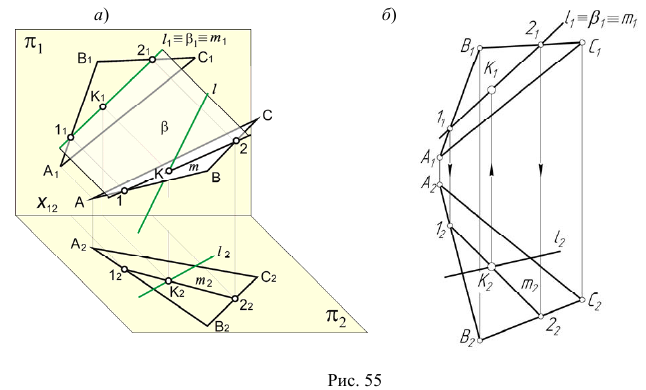
4. Определим видимость прямой 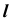
Точка K делит прямую 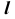
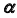
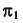
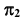
Определим видимость прямой 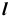
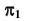
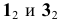
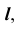
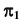
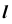
Видимость прямой 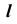
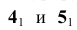
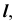
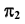
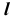
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пересечение прямой с поверхностью
- Пересечение поверхностей
- Способы преобразования чертежа
- Ортогональное проецирование: точка, прямая, плоскость
- Отображение пространственных объектов на плоскость
- Моделирование линии на эпюре Монжа
- Моделирование плоскости на эпюре Монжа
- Моделирование поверхностей на эпюре Монжа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник




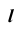
 — горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой  Отметим горизонтальную проекцию
Отметим горизонтальную проекцию 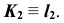
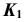 определим по принадлежности точки K плоскости
определим по принадлежности точки K плоскости 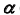 (задача 3).
(задача 3).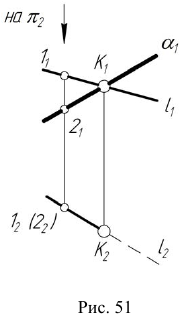
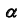 — фронтально- проецирующая, следовательно, проекция
— фронтально- проецирующая, следовательно, проекция 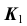 определится на пересечении фронтальных проекций прямой и плоскости
определится на пересечении фронтальных проекций прямой и плоскости 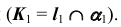
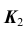 определим по принадлежности точки K прямой
определим по принадлежности точки K прямой  (задача 1).
(задача 1).
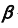 — фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости 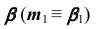 (рис. 53, б).
(рис. 53, б).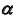 (задача 2).
(задача 2).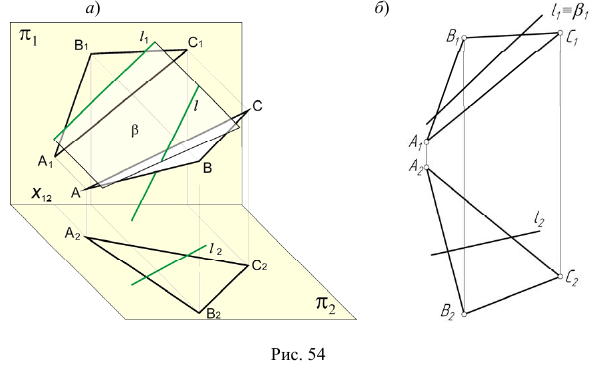
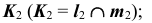
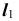 и линии проекционной связи отметим проекцию
и линии проекционной связи отметим проекцию 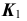 (рис. 55, б).
(рис. 55, б).