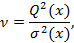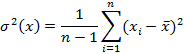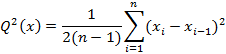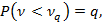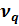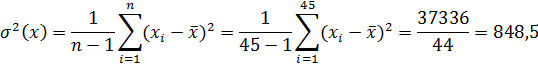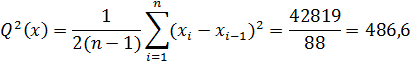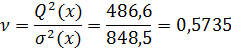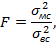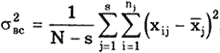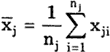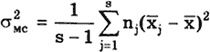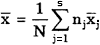Способ последовательных разностей критерий аббе
Рейтинг: 
Пример 5.2. Измерить ЭДС потенциометром постоянного тока, имеющим паразитную термоЭДС.
При выполнении одного измерения получаем ЭДС E1. Затем меняем полярность измеряемой ЭДС и направление тока в потенциометре. Вновь проводим его уравновешивание — получаем значение Е2. Если термоЭДС дает погрешность DЕ и Е1 =ЕХ + DЕ, то Е2 = ЕХ — DЕ. Отсюда Ех= (Е1 + Е2)/2. Следовательно, систематическая погрешность, обусловленная действием термоЭДС, устранена.
• Метод рандомизации — наиболее универсальный способ исключения неизвестных постоянных систематических погрешностей. Суть его состоит в том, что одна и та же величина измеряется различными методами (приборами). Систематические погрешности каждого из них для всей совокупности являются разными случайными величинами. Вследствие этого при увеличении числа используемых методов (приборов) систематические погрешности взаимно компенсируются.
Для устранения переменных и монотонно изменяющихся систематических погрешностей применяют следующие приемы и методы.
• Анализ знаков неисправленных случайных погрешностей. Если знаки неисправленных случайных погрешностей чередуются с какой-либо закономерностью, то наблюдается переменная систематическая погрешность. Если последовательность знаков «+» у случайных погрешностей сменяется последовательностью знаков»—» или наоборот, то присутствует монотонно изменяющаяся систематическая погрешность. Если группы знаков «+» и «-» у случайных погрешностей чередуются, то присутствует периодическая систематическая погрешность.
• Графический метод. Он является одним из наиболее простых способов обнаружения переменной систематической погрешности в ряду результатов наблюдений и заключается в построении графика последовательности неисправленных значений результатов наблюдений. На графике через построенные точки проводят плавную кривую, которая выражает тенденцию результата измерения, если она существует. Если тенденция не прослеживается, то переменную систематическую погрешность считают практически отсутствующей.
• Метод симметричных наблюдений. Рассмотрим сущность этого метода на примере измерительного преобразователя, передаточная функция которого имеет вид y = kx + y0, где х, у — входная и выходная величины преобразователя; k — коэффициент, погрешность которого изменяется во времени по линейному закону; у0 — постоянная.
Для устранения систематической погрешности трижды измеряется выходная величина у через равные промежутки времени Dt. При первом и третьем измерениях на вход преобразователя подается сигнал х0 от образцовой меры. В результате измерений получается система уравнений:
Ее решение позволяет получить значение х, свободное от переменной систематической погрешности, обусловленной изменением коэффициента k:
• Специальные статистические методы. К ним относятся способ последовательных разностей, дисперсионный анализ, и др. Рассмотрим подробнее некоторые из них.
Способ последовательных разностей (критерий Аббе). Применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем. Дисперсию результатов наблюдений можно оценить двумя способами: обычным
и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей (хi+1 — xi)2
Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т.е. имела место переменная систематическая погрешность, то s2[х] дает преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на s2[х] влияют вариации х . В то же время изменения центра группирования х весьма мало сказываются на значениях последовательных разностей di = (хi+1 — xi), поэтому смещения х̅ почти не отразятся на значении Q2[x].
Отношение v = Q2[x]/s2[x] является критерием для обнаружения систематических смещений центра группирования результатов наблюдений. Критическая область для этого критерия (критерия Аббе) определяется как P(v
Источник
Классификация систематических погрешностей. Способы обнаружения и устранения
1. Постоянные систематические погрешности – погрешности, которые в течение всего времени измерений сохраняют свой знак и свое значение (погрешности большинства мер, например, гирь, концевых мер длины, катушек и магазинов сопротивления).
2. Переменные погрешности при повторных измерениях могут принимать различные значения и в зависимости от характера изменения эти погрешности подразделяют на:
— прогрессивные погрешности – погрешности, которые в процессе измерений возрастают или убывают. Пример: погрешности, возникающие вследствие износа контактирующих деталей средств измерения, постепенное падение напряжения источника тока, питающего измерительную цепь;
— периодические погрешности – погрешности, значения которых являются периодической функцией времени или функцией перемещения указателя измерительного прибора. Пример: средства измерений с круговой шкалой, стрелка которых при измерении совершает несколько оборотов (секундомеры, индикаторы часового типа).
Специальные статистические способыобнаружения систематических погрешностей:
1. Способ последовательных разностей (критерий Аббе) применяется для обнаружения изменяющейся во времени систематической погрешности и состоит в следующем.
является критерием для обнаружения систематических погрешностей, где
Это две оценки дисперсии (среднего квадратического отклонения) результатов наблюдений: обычным способом и вычислением суммы квадратов последовательных (в порядке проведения измерений) разностей (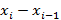 
). Отсюда и название метода.
Критическая область для критерия Аббе определяется как:
где q=1-P – уровень значимости;
Р – доверительная вероятность.
Значения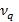 
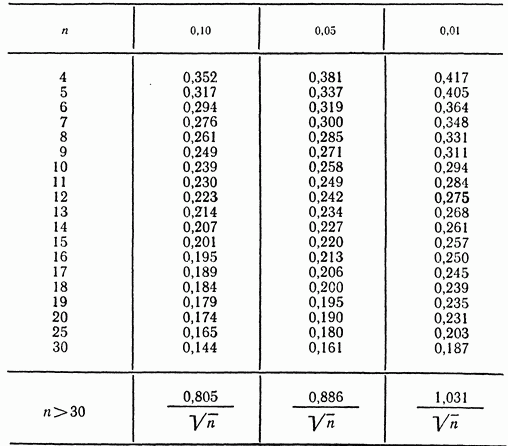
для различных уровней значимости q и числа наблюдений n приведены в таблице.
Таблица 1 – Значения критерия Аббе 
Если полученное значение критерия Аббе меньше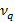 
, то обнаруживается систематическая погрешность результатов измерений.
Пример: На цементном заводе в процессе производства ежедневно в течение 45 дней брались пробы и определялось среднее сопротивление сжатию контрольных кубов (н/см 2 или кг/см 2 ). Результаты наблюдения: 40, 33, 75, 18, 62, 33, 38, 69, 65, 100, 124, 91, 79, 42, 63, 23, 47, 52, 98, 97, 73, 85, 88, 40, 42, 51, 23, 75, 52, 126, 90, 111, 92, 109, 72, 28, 56, 17, 52, 68, 75, 102, 107, 77, 45 (всего 45 измерений).
Зададимся уровнем значимости q=0,05. Из таблицы 1 находим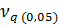 
(45) = 0,7603.
Как видно, полученное значение критерия Аббе меньше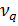 
, следовательно, присутствует систематическая погрешность результатов измерений.
2. Дисперсионный анализ (критерий Фишера) позволяет выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическую погрешность.
В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует различным значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление), временная последовательность проведения измерений и т.п.
После проведения N измерений их разбивают на s серий (s>3) по nj результатов наблюдений в каждой серии и затем устанавливают, имеетсяили отсутствует систематическое расхождение между результатаминаблюдений в различных сериях.
Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера:
где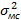 
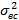
– межсерийная дисперсия, выражает силу действия фактора, вызывающего систематические различия между сериями;
– внутрисерийная дисперсия, характеризует случайные погрешности измерений, обуславливающие различия (отклонения результатов наблюдений) внутри серии.
Критическая область для критерия Фишера соответствует P(F > Fq) = q.
Значения Fq для различных уровней значимости q, числа измерений N и числа серий s приведены в таблице 2.
Таблица 2 — Значения критерия Фишера
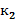 | Fq при к1, равном | ||||||
| 98,49 | 99,00 | 99,17 | 99,25 | 99,30 | 99,33 | 99,36 | 99,42 |
| 21,20 | 18,00 | 16,69 | 15,98 | 15,52 | 15,21 | 14,80 | 14,37 |
| 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,10 | 7,72 |
| 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,03 | 5,67 |
| 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,06 | 4,71 |
| 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,50 | 4,16 |
| 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,14 | 3,80 |
| 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,20 | 3,89 | 3,55 |
| 8,28 | 6,01 | 5,09 | 4,58 | 4,25 | 4,01 | 3,71 | 3,37 |
| 8,10 | 5,85 | 4,94 | 4,43 | 4,10 | 3,87 | 3,56 | 3,23 |
| 7,56 | 5,39 | 4,51 | 4,02 | 3,70 | 3,47 | 3,17 | 2,84 |
Для определения Fq необходимо вычислить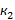 
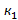
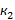
= N-s и 
= s-1. Причем, – это число степеней свободы большей дисперсии, к1– число степеней свободы меньшей дисперсии.
Если полученное значение критерия Фишера больше Fq, то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
Дисперсионный анализ (критерий Фишера) является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.
Дисперсионный анализ (критерий Фишера). В практике измерений часто бывает необходимо выяснить наличие систематической погрешности результатов наблюдений, обусловленной влиянием какого-либо постоянно действующего фактора, или определить, вызывают ли изменения этого фактора систематическое смещение результатов измерений. В данном случае проводят многократные измерения, состоящие из достаточного числа серий, каждая из которых соответствует определенным (пусть неизвестным, но различным) значениям влияющего фактора. Влияющими факторами, по которым производится объединение результатов наблюдений по сериям, могут быть внешние условия (температура, давление и т.д.), временная последовательность проведения измерений и т.п. 
После проведения N измерений их разбивают на s серий (s > 3) поnj результатов наблюдений ( snj= N ) в каждой серии и затем устанавливают, имеется или отсутствует систематическое расхождение между результатами наблюдений в различных сериях. При этом должно быть установлено, что результаты в сериях распределены нормально. Рассеяние результатов наблюдений в пределах каждой серии отражает только случайные влияния, характеризует лишь случайные погрешности измерений в пределах этой серии. Характеристикой совокупности случайных внутрисерийных погрешностей будет средняя сумма дисперсий результатов наблюдений, вычисленных раздельно для каждой серии, т.е.
где xji — результат i-го измерения в j-й серии.
Внутрисерийная дисперсия 
2 BC характеризует случайные погрешности измерений, так как только случайные влияния обусловливают те различия (отклонения результатов наблюдений), на которых она основана. В то же время рассеяние 
j различных серий обусловливается не только случайными погрешностями измерений, но и систематическими различиями (если они существуют) между результатами наблюдений, сгруппированными по сериям. Следовательно, усредненная межсерийная дисперсия
где , выражает силу действия фактора, вызывающего систематические различия между сериями.
Таким образом, 2 BC /( 2 BC+ 2 MC) характеризует долю дисперсии всех результатов наблюдений, обусловленную наличием случайных погрешностей измерений, а 2 MC /( 2 BC+ 2 MC) — долю дисперсии, обусловленную межсерийными различиями результатов наблюдений. Первую из них называют коэффициентом ошибки, вторую — показателем дифференциации. Чем больше отношение показателя дифференциации к коэффициенту ошибки, тем сильнее действие фактора, по которому группировались серии, и тем больше систематическое различие между ними.
Критерием оценки наличия систематических погрешностей в данном случае является дисперсионный критерий Фишера F= 2 MC 2 BC. Критическая область для критерия Фишера соответствует P(F>Fq)=q.
Значения Fq для различных уровней значимости q, числа измерений N и числа серий s приведены в приложении 1, где k2=N-s , k1=s-1. Если полученное значение критерия Фишера больше Fq (при заданных q, N и s), то гипотеза об отсутствии систематических смещений результатов наблюдений по сериям отвергается, т.е. обнаруживается систематическая погрешность, вызываемая тем фактором, по которому группировались результаты наблюдений.
Из всех рассмотренных способов обнаружения систематических погрешностей дисперсионный анализ является наиболее эффективным и достоверным, так как позволяет не только установить факт наличия погрешности, но и дает возможность проанализировать источники ее возникновения.
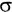
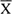
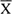
Дата добавления: 2016-05-28 ; просмотров: 6893 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник
