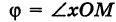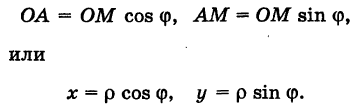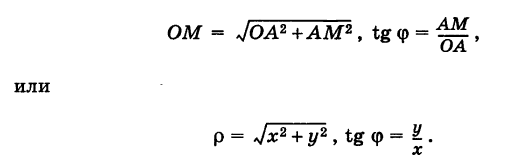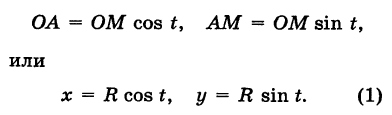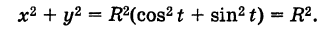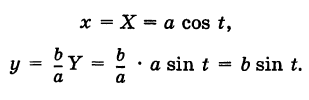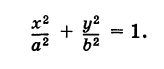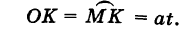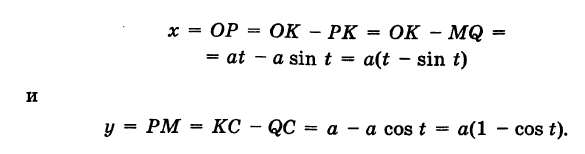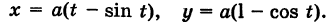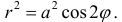Способы геодезических разбивочных работ

Drillings.ru

Торговый дом АУМАС

Тел: +7 (8552) 77-36-15
Моб. тел.: +79053740010, +79600530909, +79656296455
E-mail: drillings@aumas.ru, sale@aumas.ru

Буровые установки (агрегаты, станки) шпиндельного типа

Глубина бурения, м

100 м

300 м

500 м

800 м

2000 м

Буровые установки с подвижным вращателем

Глубина бурения, м

до 15 м.

до 25-50 м.

до 100 м.

до 300 м.

до500 м.

до1000 м.

до2000 м.

Буровые установки роторного типа для бурения скважин

Глубина бурения, м

до 25-50 м.

до 200 м.

600-800 м.

Глубина бурения 2000-3000 м.

Самоходные буровые установки для бурения скважин

Буровые установки и оборудование для глубокого бурения

Источник

ТЕМА 11: «ТОПОГЕОДЕЗИЧЕСКАЯ ПРИВЯЗКА ПО КАРТЕ»

от Admin

ЗАНЯТИЕ 2: «ПОЛЯРНЫЙ СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ»

Вопрос I. Условия применения, сущность полярного способа.

Полярный способ применяется в условиях прямой видимости между контурной (исходной) и привязываемой точками.

Сущность полярного способа заключается в определении дирекционного угла направления с исходной контурной точки на привязываемую и расстояния между ними, вычислении координат привязываемой точки решением ПГЗ.

Дирекционный угол с исходной точки на привязываемую определяют способом, обеспечивающим наибольшую точность и своевременность в данных условиях обстановки.

Если прибор устанавливается не на исходной , а на привязываемой точке, то измеренный с нее дирекционный угол на исходную точку изменяют на 30-00.

Расстояние от исходной точки до привязываемой измеряют мерной лентой , с помощью дальномерной рейки , дальномерами , засечкой с помощью базы.

Вычисление координат привязываемой точки сводится к решению ПГЗ с помощью приборов ,таблиц приращений координат.

На МК: Хпр= Хисх + Д cosaисх-пр;

Упр= Уисх + Д sinaисх-пр.

На АЛЛ:Хпр = Хисх + Д sin(15-00 — a¢исх-пр);

Упр= Уисх + Д sin a¢исх-пр.

Для контроля координаты привязываемой точки определяют этим же способом относительно другой контурной точки.

Разница координат не должна превышать:

-25м для карты М 1:25000 ( аэрофотоснимка );

-50м для карты М 1:50000;

-100м для карты М 1:100000.

За окончательный результат принимают среднее значение двух вычислений. В случае превышения указанных значений проверяют вычисления или повторяют полевые измерения.

Определить координаты ОП при ТГП полярным способом от КТ с отм.193,6 (7111), если aкт-оп=26-80, расстояние Дкт-оп измерено буссолью с помощью дальномерной рейки и равно 250м.

1.Определить прямоугольные координаты отм.193,6 (7111) по карте:

2.Вычислить a¢ = 30-00 — a = 30-00-26-80 = 3-20.
3.Вычислить приращения координат:

DХ = Д sin(15-00 — a¢кт-оп) = 250 sin12-80 = — 236м;

DY = Д sin a¢кт-оп = 250 sin 3-20 = + 82м.

4.Вычислить координаты ОП:

Хоп = Хкт + DХ = 71705-236= 71469;

Уоп = Укт + DУ = 11272+82= 11354.

5.Нанести ОП на карту .( h=195м).

Определить координаты ОП от КТ отм.176,2 (6908), если aоп-кт=1-30, расстояние ОП-КТ измерено буссолью с помощью дальномерной рейки

1.Определить прямоугольные координаты отм.176,2 (6909) по карте:
Хкт=69530, Укт=08840.

2.Изменить дирекционный угол с ОП на КТ на обратный:

aкт-оп = aоп-кт ± 30-00 = 1-30 ± 30-00 = 31-30.

3.Вычислить a¢=31-30 — a = 31-30-30-00 = 1-30.

3.Вычислить приращения координат:

DХ = Д sin(15-00 — a¢кт-оп) = 247 sin13-70 = — 245м;

DY = Д sin a¢кт-оп = 247 sin 1-30 = — 33м.

4.Вычислить координаты ОП:

Хоп = Хкт + DХ = 69530-245 = 69385;

Уоп = Укт + DУ = 08840-33 = 08807.

5.Нанести ОП на карту .

В том случае, когда расстояние до начальной точки более 400 м, отсутствует дальномер, невозможно определить другим способом , расстояние определяют засечкой с помощью базы.

База может располагаться под прямым углом или острым углом

Вопрос 2. Полярный способ определения координат с вычислением дальности засечкой с помощью базы.

При невозможности расположить базу под прямым углом, ее можно выбросить под любым углом в то место, откуда будет наблюдаться контурная точка.

В практике топогеодезических работ привязка элементов боевого порядка полярным способом с вычислением дальности засечкой с помощью базы сводится к решению треугольника по двум углам и одной стороне ( базе).

Согласно теоремы синусов: в треугольнике отношение длины любой стороны к синусу противолежащего ей угла есть величина постоянная.

Поэтому для треугольника АВС можно записать соотношение

АВ/sinC = AC/sinB = BC/sinA.

Порядок проведения полевых измерений

1. Расставить ПАБ в стороне от привязываемой точки (Р), так чтобы направление базы было примерно перпендикулярно к направлению НТ.
2. Сориентировать ПАБ по дирекционному углу и измерить:

— дирекционный угол с ПАБ на НТ (aпаб-нт);

— дирекционный угол на ОП (aпаб-р).

1. Измерить длину базы Б.
2. Измерить горизонтальный угол b с привязываемой точки (Р) между направлениями на НТ и ПАБ.

Можно определить b по панораме орудия, если ОП уже занята.

1. Если ОП не занята, то над привязываемой точкой расставить буссоль, сориентировать ее по дирекционному углу и измерить дирекционный угол на начальную точку.

Обработка результатов полевых измерений

1).Определить по карте координаты НТ (Хнт, Унт).

2).Вычислить горизонтальный угол при буссоли Q.

Он равен разнице между дирекционными углами правого и левого

Q = aпаб-р — aпаб-нт

3). Вычислить горизонтальный угол при НТ — угол засечки g.

4). Вычислить дальность Д

Д=Б/sing sinQ

5.) Вычислить дирекционный угол с НТ на привязываемую точку Р:

a нт-р = (aпаб-нт± 30-00)±g,

где знак «+» или «-» угла засечки определяется из абриса.

6). Решением ПГЗ вычислить приращения координат от НТ к привязываемой точке DХ и DУ.

7). Вычислить координаты привязываемой точки Р.

Определить координаты ОП полярным способом по карте М 1:50000 от НТ — труба черепичного завода (7110). Дальность до НТ определить засечкой с помощью базы, если база расположена под острым углом к измеряемому расстоянию.

aпаб-оп=51-81, aпаб-нт=6-60, Б = 62 м, b=13-89

1.Определить с карты Хнт = 71505 , Унт=10735.

2.Q=aпаб-нт — aпаб-оп = 66-60 — 51-81 = 14-79.

4.Д=Б/sing sinQ = sin14-79 = 450м.

5.aнт-оп = (aпаб-нт±30-00) ±g = (6-00+30-00) + 1-32 = 37-92,

где знак «+»- определен по абрису, a¢=7-92.

6.DХ=Д sin(15-00 — a¢нт-оп) = 450 sin(15-00-7-92) = -304м;

Источник

Полярные координаты — определение и вычисление с примерами решения

Содержание:

Полярные координаты. параметрические уравнения линии

Полярные координаты

Основная идея метода координат состоит в том, что положение точки на плоскости однозначно определяется с помощью двух чисел. Конкретный геометрический смысл этих чисел дает ту или иную систему координат. Наиболее важной после прямоугольной системы, исключительно употреблявшейся нами до сих пор, является полярная система координат, к рассмотрению которой мы и переходим.

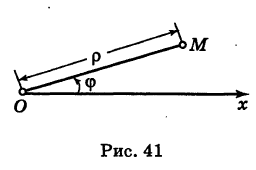
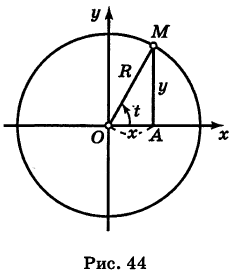
Возьмем на плоскости точку О, которую назовем полюсом. Проведем из полюса О направленную полупрямую Ох, называемую полярной осью (рис. 41).

Пусть М — произвольная точка плоскости. Соединим точку М с полюсом О отрезком ОМ. Длина отрезка ОМ = р называется полярным радиусом точки М, а угол

Точка М с полярными координатами риф записывается следующим образом: М (р, ф), причем на первом месте ставится полярный радиус р, а на втором — полярный угол ф.

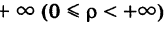
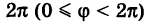
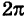
Что касается значений, принимаемых полярными координатами, то достаточно, очевидно, рассматривать значения р от 0 до и значения ф от 0 до , при этом, как мы условились, угол ф отсчитывается от полярной оси против хода часовой стрелки. Однако в некоторых вопросах приходится рассматривать углы, большие , а также отрицательные углы, т. е. углы, отсчитываемые от полярной оси по направлению движения часовой стрелки.

Связь между прямоугольными и полярными координатами

Рассмотрим переход от полярных координат к прямоугольным и обратно.

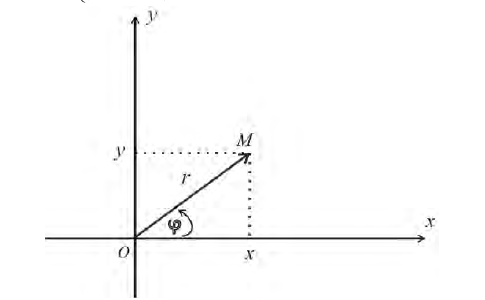
Предположим, что полюс полярной системы совпадает с началом прямоугольной системы координат Оху, а полярная ось является положительной полуосью Ох (рис. 42).

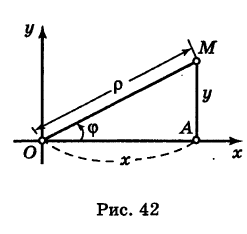
Тогда для произвольной точки М имеем

Считая угол ф острым, из прямоугольного треугольника АОМ находим

Полученные формулы справедливы для любого угла ф. Так выражаются прямоугольные координаты точки М через ее полярные координаты. Далее, из этого же прямоугольного треугольника АОМ получаем

Так выражаются полярные координаты точки через ее прямоугольные координаты.

Заметим, что при определении полярного угла ф по tg ф нужно учитывать знаки координат х и у.

Ранее мы видели, что линии могут быть заданы с помощью уравнений, связывающих их текущие прямоугольные координаты. Покажем теперь на простейшем примере, что линии могут определяться и уравнениями относительно полярных координат.

Пример:

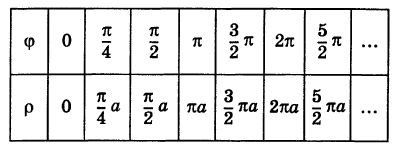
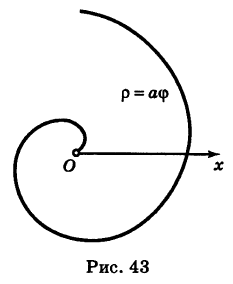
Рассмотрим кривую 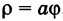, где а — некоторое положительное число. Эта кривая называется спиралью Архимеда. Для ее построения составляем таблицу соответственных значений ф и р:

По этой таблице наносим точки и соединяем их линией, уточняя, если в этом есть необходимость, положение промежуточных точек (рис. 43).

Параметрические уравнения линии

Иногда бывает удобнее вместо уравнения линии, связывающего прямоугольные координаты 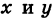, рассматривать так называемые параметрические уравнения линии, дающие выражения текущих координат х и у в виде функций от некоторой переменной величины t (параметра). Параметрические уравнения играют важную роль, например, в механике, где координаты х и у движущейся точки М (х, у) рассматриваются как функции времени (уравнения движения).

Пример:

Выведем параметрические уравнения окружности.

Пусть М 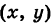— произвольная точка окружности радиуса R с центром в начале координат (рис. 44). В определяемом ею прямоугольном треугольнике АОМ обозначим угол хОМ через t. Тогда, очевидно, будут иметь место равенства

Это и есть параметрические уравнения окружности.

Чтобы получить обычное уравнение окружности, нужно исключить параметр t. Для этого возводим уравнения (1) в квадрат и складываем их:

Пример:

Выведем параметрические уравнения эллипса.

Эллипс с полуосями а и b можно рассматривать как равномерно сжатую вдоль вертикального диаметра окружность радиуса а, где коэффициент сжатия k = b/a. Пусть М (х, у) — точка эллипса, N (X, У) — соответствующая точка окружности (рис. 45), где

За параметр t примем угол, образованный радиусом ON окружности с положительным направлением оси Ох: . Используя формулы (2), имеем

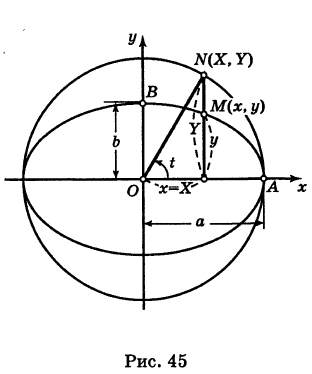
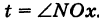
Таким образом, параметрические уравнения эллипса с полуосями а и b есть

Исключив из уравнений (3) параметр получим каноническое уравнение эллипса

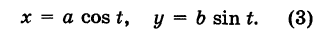
Имея параметрические уравнения линии, можно по точкам построить ее.

Пример:

Решение:

Составляем таблицу значений:

Нанося точки с соответствующими координатами (х, у) на плоскость Оху и соединяя их линией, получим искомую кривую (рис. 46).

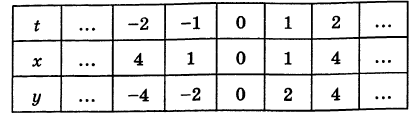
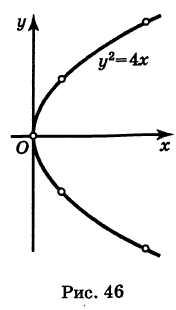
Эта кривая— парабола. В самом деле, исключив параметр t из уравнений (4), получим 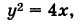т. е. каноническое уравнение параболы.

Параметрические уравнения циклоиды

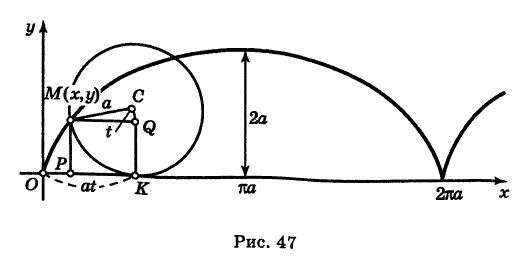
Определение: Циклоидой называется кривая, описываемая точкой окружности, катящейся без скольжения по прямой линии (рис. 47).

Выведем параметрические уравнения циклоиды, приняв прямую за ось Ох, предполагая, что радиус катящейся окружности равен айв начальном положении движущаяся точка М совпадает с началом координат. За параметр t примем угол поворота (в радианах) подвижного радиуса МС окружности относительно вертикального радиуса КС, где К — точка касания окружности с осью Ох (рис. 47). Так как качение окружности происходит без скольжения, то, очевидно, имеем

Отсюда на основании рис. 47 для координат текущей точки М циклоиды получаем следующие выражения:

Таким образом, параметрические уравнения циклоиды есть

Полярная система координат

Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат Оху . Пусть М(х, у) – точка на плоскости, M ≠ 0. Полярными координатами точки М называются числа r − длина ее радиус-вектора (полярный
радиус) и ϕ − угол, образованный радиус-вектором с положительным направлением оси Ох (полярный угол), 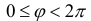. Точка О при этом называется
полюсом, а полуось Ох – полярной осью.
Замечание. Зависимость между прямоугольными (х, у) и полярными ( , ) r ϕ
координатами точки М задается в виде: 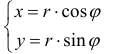(1)

Рис.1. Полярные координаты точки.
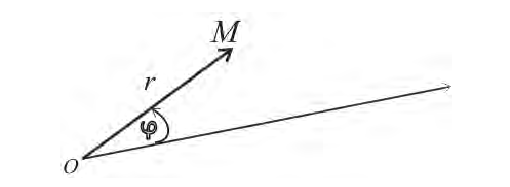
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя
прямоугольную систему координат:

Пример 1.

Построим на плоскости линию, заданную уравнением:
− лемниската.
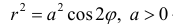
Решение.

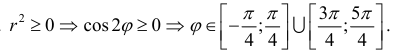
Вычислим значения r при различных значениях ϕ :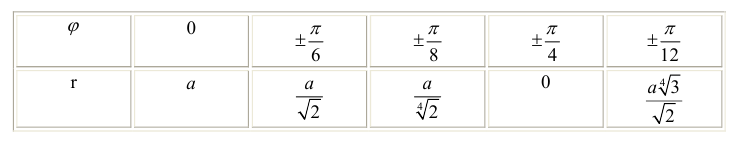

Проводим лучи из начала координат под углами ϕ к оси Ох и на них откладываем
отрезки длины r , получим :

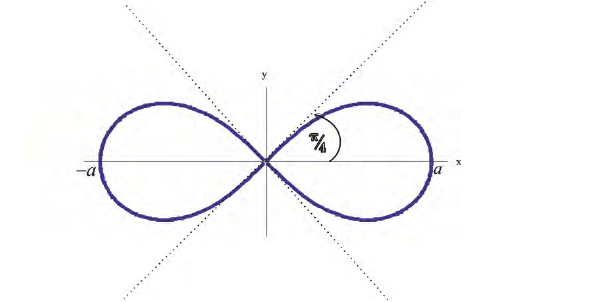
Рис.3. Лемниската

Пример 2.

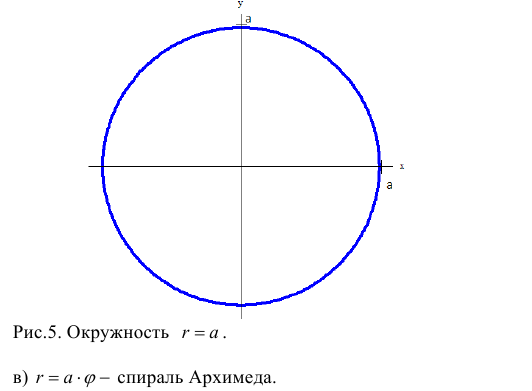
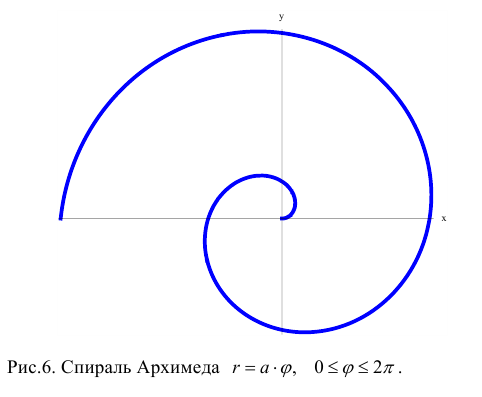
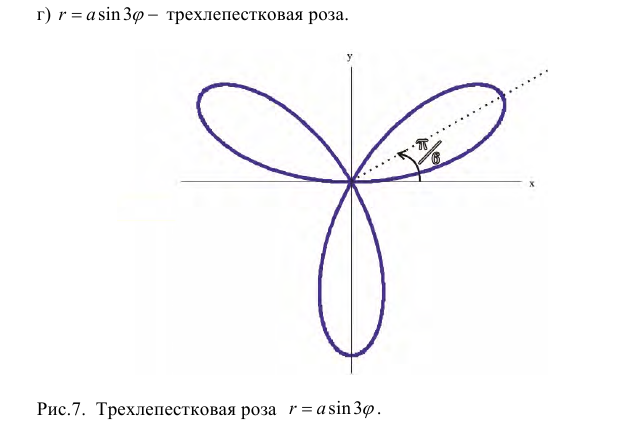
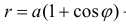
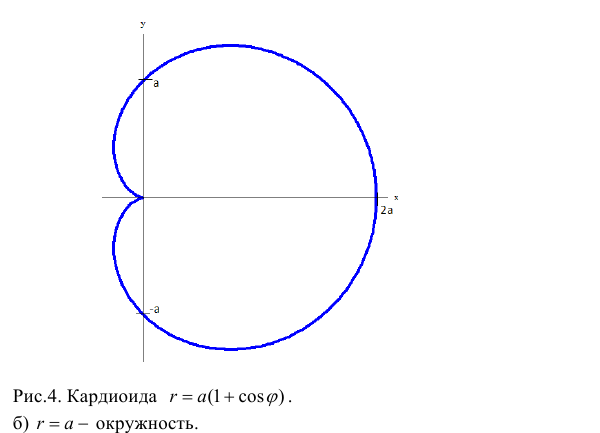
а) Построим кривую − кардиоида. Рассуждая, как в примере 1 получим:




Замечание. Если в определении 1 отбросить требование 0 ≤ ϕ 0, то формулы (1) будут задавать непрерывное отображение точек плоскости (O, r, ϕ) на точки плоскости (x, O, y).

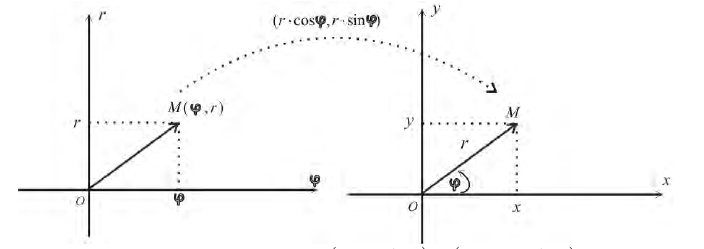
При этом, если r > 0, то векторы 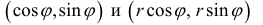сонаправлены, если r

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник