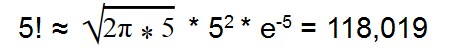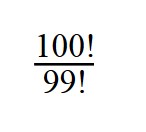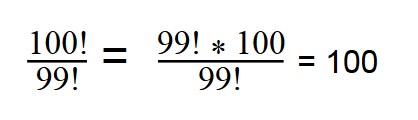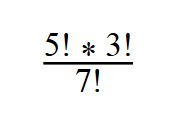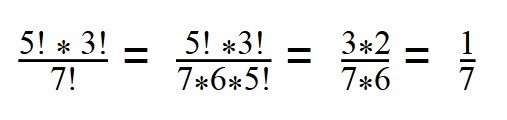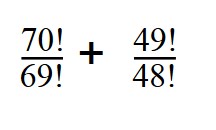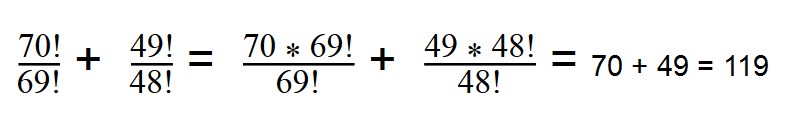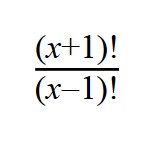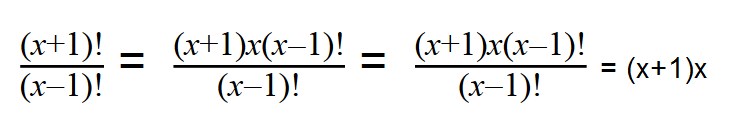- Способ получить факториал
- Альтернативные вопросы в кроссвордах для слова умножение
- Определение слова умножение в словарях
- Примеры употребления слова умножение в литературе.
- Факториал
- Факториал: определение
- Формулы и свойства факториала
- Примеры решений
- Способ получить произведение
- Альтернативные вопросы в кроссвордах для слова умножение
- Определение слова умножение в словарях
- Примеры употребления слова умножение в литературе.
- Алгоритмы быстрого вычисления факториала
Способ получить факториал
Последняя бука буква «е»
Ответ на вопрос «Способ получить факториал «, 9 (девять) букв:
умножение
Альтернативные вопросы в кроссвордах для слова умножение
Определение слова умножение в словарях
Википедия Значение слова в словаре Википедия
Умноже́ние — одна из основных бинарных математических операций ( арифметических действий) двух аргументов . Например для натуральных чисел: $c=a \cdot b = \underbrace< a+a+\cdots+a >_= a_1 + a_2 + \ldots + a_b = <\displaystyle\sum_
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова. Значение слова в словаре Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
-я, ср. см. множить, -ся. Математическое действие посредством к-рого из двух чисел (или величин) получается новое число (или величина), к-рое (для целых чисел) содержит слагаемым первое число столько раз, сколько единиц во втором. Таблица умножения. Задача.
Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
арифметическое действие. Обозначается точкой «.» или знаком «?» (в буквенном исчислении знаки умножения опускаются). Умножение целых положительных чисел (натуральных чисел) есть действие, позволяющее по двум числам а (множимому) и b (множителю) найти третье.
Примеры употребления слова умножение в литературе.
Он сравнивает их дело также с заквашиванием, с сеянием семян и с умножением горчичных зерен.
Затем были и те, кто не решался вмешиваться вообще, потому что сознание их исследовало события вторичных и третьестепенных эффектов по мере их умножения и запутывания по всем направлениям всей системы.
За прошедшее столетие вновь произошло умножение грехов и сниже-ние греховного порога в результате внедрившегося в умы людей антих-риста в виде материалистическо-атеистического учения и лжепророка в лице Коммунистической партии Маркса -Ленина.
За прошедшее столетие вновь произошло умножение грехов и сниже-ние греховного порога в результате внедрившегося в умы людей антих-риста в виде материалистическо-атеистического учения и лжепророка в лице Коммунистической партии Маркса-Ленина.
Это критика доктрины меркантилизма, отождествлявшей умножение количества денег в стране с ростом благосостояния населения.
Источник: библиотека Максима Мошкова
Источник
Факториал
О чем эта статья:
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
- 3! 56! 12!
| Формула факториала n!=1⋅2⋅3⋅. ⋅(n−2)⋅(n−1)⋅n |
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
- (n — 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)
- n! = 1*2*3*4*5*. *(n — 2)(n — 1)n
- (n + 1)! = 1*2*3*4*5*. *(n — 2)(n — 1)n(n + 1)
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
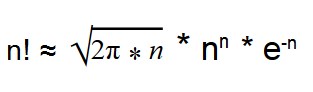 |
Рекуррентная формула
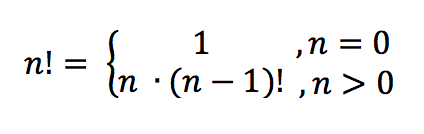 |
- 5! = 5*(5 — 1)! = 5*4! = 5*24 = 120
- 6! = 6*(6-1)! = 6*5! = 6*120 = 720
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
- Пользуйтесь готовой таблицей 5! * 7! = 120 * 5040 = 604800
- Или раскладывайте факториалы отдельно, если хотите потренироваться:
5! = 1*2*3*4*5 = 4! * 5 =120
7! = 1*2*3*4*5*6*7 = 6! * 7 = 5040
120 * 5040 = 604800
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
При сокращении факториалов, пользуйтесь свойством:
n! = (n — 1)! * n
100! = 99! * 100
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.
Источник
Способ получить произведение
Последняя бука буква «е»
Ответ на вопрос «Способ получить произведение «, 9 (девять) букв:
умножение
Альтернативные вопросы в кроссвордах для слова умножение
Определение слова умножение в словарях
Википедия Значение слова в словаре Википедия
Умноже́ние — одна из основных бинарных математических операций ( арифметических действий) двух аргументов . Например для натуральных чисел: $c=a \cdot b = \underbrace< a+a+\cdots+a >_= a_1 + a_2 + \ldots + a_b = <\displaystyle\sum_
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова. Значение слова в словаре Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
ср. Процесс действия по знач. глаг.: умножать (1), умножить. Состояние по знач. глаг.: умножаться (1), умножиться. Арифметическое действие, повторение определенного числа в качестве слагаемого столько раз, сколько единиц содержится в другом числе.
Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
арифметическое действие. Обозначается точкой «.» или знаком «?» (в буквенном исчислении знаки умножения опускаются). Умножение целых положительных чисел (натуральных чисел) есть действие, позволяющее по двум числам а (множимому) и b (множителю) найти третье.
Примеры употребления слова умножение в литературе.
Он сравнивает их дело также с заквашиванием, с сеянием семян и с умножением горчичных зерен.
Затем были и те, кто не решался вмешиваться вообще, потому что сознание их исследовало события вторичных и третьестепенных эффектов по мере их умножения и запутывания по всем направлениям всей системы.
За прошедшее столетие вновь произошло умножение грехов и сниже-ние греховного порога в результате внедрившегося в умы людей антих-риста в виде материалистическо-атеистического учения и лжепророка в лице Коммунистической партии Маркса -Ленина.
За прошедшее столетие вновь произошло умножение грехов и сниже-ние греховного порога в результате внедрившегося в умы людей антих-риста в виде материалистическо-атеистического учения и лжепророка в лице Коммунистической партии Маркса-Ленина.
Это критика доктрины меркантилизма, отождествлявшей умножение количества денег в стране с ростом благосостояния населения.
Источник: библиотека Максима Мошкова
Источник
Алгоритмы быстрого вычисления факториала
Понятие факториала известно всем. Это функция, вычисляющая произведение последовательных натуральных чисел от 1 до N включительно: N! = 1 * 2 * 3 *… * N. Факториал — быстрорастущая функция, уже для небольших значений N значение N! имеет много значащих цифр.
Попробуем реализовать эту функцию на языке программирования. Очевидно, нам понадобиться язык, поддерживающий длинную арифметику. Я воспользуюсь C#, но с таким же успехом можно взять Java или Python.
Итак, простейшая реализация (назовем ее наивной) получается прямо из определения факториала:
На моей машине эта реализация работает примерно 1,6 секунд для N=50 000.
Далее рассмотрим алгоритмы, которые работают намного быстрее наивной реализации.
Алгоритм вычисления деревом
Первый алгоритм основан на том соображении, что длинные числа примерно одинаковой длины умножать эффективнее, чем длинное число умножать на короткое (как в наивной реализации). То есть нам нужно добиться, чтобы при вычислении факториала множители постоянно были примерно одинаковой длины.
Пусть нам нужно найти произведение последовательных чисел от L до R, обозначим его как P(L, R). Разделим интервал от L до R пополам и посчитаем P(L, R) как P(L, M) * P(M + 1, R), где M находится посередине между L и R, M = (L + R) / 2. Заметим, что множители будут примерно одинаковой длины. Аналогично разобьем P(L, M) и P(M + 1, R). Будем производить эту операцию, пока в каждом интервале останется не более двух множителей. Очевидно, что P(L, R) = L, если L и R равны, и P(L, R) = L * R, если L и R отличаются на единицу. Чтобы найти N! нужно посчитать P(2, N).
Посмотрим, как будет работать наш алгоритм для N=10, найдем P(2, 10):
P(2, 10)
P(2, 6) * P(7, 10)
( P(2, 4) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( (P(2, 3) * P(4) ) * P(5, 6) ) * ( P(7, 8) * P(9, 10) )
( ( (2 * 3) * (4) ) * (5 * 6) ) * ( (7 * 8) * (9 * 10) )
( ( 6 * 4 ) * 30 ) * ( 56 * 90 )
( 24 * 30 ) * ( 5 040 )
720 * 5 040
3 628 800
Получается своеобразное дерево, где множители находятся в узлах, а результат получается в корне
Реализуем описанный алгоритм:
Для N=50 000 факториал вычисляется за 0,9 секунд, что почти вдвое быстрее, чем в наивной реализации.
Алгоритм вычисления факторизацией
Второй алгоритм быстрого вычисления использует разложение факториала на простые множители (факторизацию). Очевидно, что в разложении N! участвуют только простые множители от 2 до N. Попробуем посчитать, сколько раз простой множитель K содержится в N!, то есть узнаем степень множителя K в разложении. Каждый K-ый член произведения 1 * 2 * 3 *… * N увеличивает показатель на единицу, то есть показатель степени будет равен N / K. Но каждый K 2 -ый член увеличивает степень еще на единицу, то есть показатель становится N / K + N / K 2 . Аналогично для K 3 , K 4 и так далее. В итоге получим, что показатель степени при простом множителе K будет равен N / K + N / K 2 + N / K 3 + N / K 4 +…
Для наглядности посчитаем, сколько раз двойка содержится в 10! Двойку дает каждый второй множитель (2, 4, 6, 8 и 10), всего таких множителей 10 / 2 = 5. Каждый четвертый дает четверку (2 2 ), всего таких множителей 10 / 4 = 2 (4 и 8). Каждый восьмой дает восьмерку (2 3 ), такой множитель всего один 10 / 8 = 1 (8). Шестнадцать (2 4 ) и более уже не дает ни один множитель, значит, подсчет можно завершать. Суммируя, получим, что показатель степени при двойке в разложении 10! на простые множители будет равен 10 / 2 + 10 / 4 + 10 / 8 = 5 + 2 + 1 = 8.
Если действовать таким же образом, можно найти показатели при 3, 5 и 7 в разложении 10!, после чего остается только вычислить значение произведения:
10! = 2 8 * 3 4 * 5 2 * 7 1 = 3 628 800
Осталось найти простые числа от 2 до N, для этого можно использовать решето Эратосфена:
Эта реализация также тратит примерно 0,9 секунд на вычисление 50 000!
Как справедливо отметил pomme скорость вычисления факториала на 98% зависит от скорости умножения. Попробуем протестировать наши алгоритмы, реализовав их на C++ с использованием библиотеки GMP. Результаты тестирования приведены ниже, по ним получается что алгоритм умножения в C# имеет довольно странную асимптотику, поэтому оптимизация дает относительно небольшой выигрыш в C# и огромный в C++ с GMP. Однако этому вопросу вероятно стоит посвятить отдельную статью.
Все алгоритмы тестировались для N равном 1 000, 2 000, 5 000, 10 000, 20 000, 50 000 и 100 000 десятью итерациями. В таблице указано среднее значение времени работы в миллисекундах.
График с линейной шкалой
График с логарифмической шкалой
Идеи и алгоритмы из комментариев
Хабражители предложили немало интересных идей и алгоритмов в ответ на мою статью, здесь я оставлю ссылки на лучшие из них
Исходные коды реализованных алгоритмов приведены под спойлерами
Источник