Способ получения когерентных волн зеркала френеля

Способы получения когерентных лучей

Для осуществления интерференции света необходимо получить когерентные световые пучки, для чего применяются различные приемы. До появления лазеров во всех приборах для наблюдения интерференции света когерентные пучки получали разделением и последующим сведением световых лучей, исходящих из одного и того же источника. Практически это можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел.

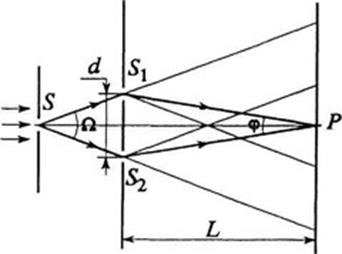
1.Метод Юнга. Свет от ярко освещенной щели S падает на две щели S1 и S2, играющие роль когерентных источников. Интерференционная картина наблюдается на экране, расположенном на некотором расстоянии параллельно S1 и S2.

Рис.2 – Интерференционная картина, полученная методом Юнга.

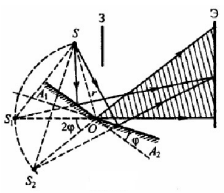
2.Зеркала Френеля. Свет от источника S падает рассеивающимися пучком на два плоских зеркала А1О и А2О, расположенных под малым углом φ. Роль когерентных источников играют мнимые S1 и S2 изображения источника S. Интерференционная картина наблюдается на экране Э, защищенном от прямого попадания света заслонкой З.

Рис.3 – Зеркала Френеля.

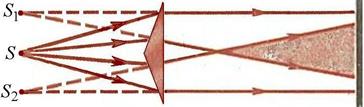
3.Бипризма Френеля. Свет от источника S преломляется в призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых когерентных источников S1 и S2. На поверхности экрана Э в заштрихованной области происходит наложение когерентных пучков и наблюдается интерференционная картина.

Рис.4 – Бипризма Френеля.

Кольца Ньютона.

Кольца Ньютона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину.

Интерференционная картина в виде концентрических колец (колец Ньютона) возникает между поверхностями, одна из которых плоская, а другая имеет большой радиус кривизны (например, стеклянная пластинка и плосковыпуклая линза). Исаак Ньютон, исследовав их в монохроматическом и белом свете, обнаружил, что радиус колец возрастает с увеличением длины волны (от фиолетового к красному).

2.3. Интерференция в тонких пленках.

Интерференцию света по методу деления амплитуды во многих отношениях наблюдать проще, чем в опытах с делением волнового фронта. Один из способов, использующих такой метод, – опыт Поля.

В опыте Поля свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки (рис.5).

В любую точку P, находящуюся с той же стороны от пластинки, что и источник, приходят два луча. Эти лучи образуют интерференционную картину.

Рис.5 – Свет от источника S отражается двумя поверхностями тонкой прозрачной плоскопараллельной пластинки.

Для определения вида полос можно представить себе, что лучи выходят из мнимых изображений S₁ и S₂ источника S, создаваемых поверхностями пластинки. На удаленном экране, расположенном параллельно пластинке, интерференционные полосы имеют вид концентрических колец с центрами на перпендикуляре к пластинке, проходящем через источник S. Этот опыт предъявляет менее жесткие требования к размерам источника S, чем рассмотренные выше опыты. Поэтому можно в качестве S применить ртутную лампу без вспомогательного экрана с малым отверстием, что обеспечивает значительный световой поток. С помощью листочка слюды (толщиной 0,03 – 0,05 мм) можно получить яркую интерференционную картину прямо на потолке и на стенах аудитории. Чем тоньше пластинка, тем крупнее масштаб интерференционной картины, т.е. больше расстояние между полосами.

Особенно важен частный случай интерференции света, отраженного двумя поверхностями плоскопараллельной пластинки, когда точка наблюдения P находится в бесконечности, т.е. наблюдение ведется либо глазом, аккомодированным на бесконечность, либо на экране, расположенном в фокальной плоскости собирающей линзы (рис.6).

Рис.6 – Полосы равного наклона.

В этом случае оба луча, идущие от S к P, порождены одним падающим лучом и после отражения от передней и задней поверхностей пластинки параллельны друг другу. Оптическая разность хода между ними в точке P такая же, как на линии DC. олоса, соответствующая данному порядку интерференции, обусловлена светом, падающим на пластинку под вполне определенным углом α. Поэтому такие полосы называют интерференционными полосами равного наклона. Если ось объектива расположена перпендикулярно пластинке, полосы имеют вид концентрических колец с центром в фокусе, причем в центре картины порядок интерференции максимален.

Полосы равного наклона можно получить не только в отраженном свете, но и в свете, прошедшем сквозь пластинку. В этом случае один из лучей проходит прямо, а другой – после двух отражений на внутренней стороне пластинки. Однако видимость полос при этом низкая.

По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной.

Явление интерференции волн, рассеянных от некоторого объекта (или прошедших через него) с «опорной» волной, лежит в основе голографии (в т.ч. оптической, акустической или СВЧ–голографии).

Интерференционные волны от отдельных «элементарных» излучателей используются при создании сложных излучающих систем (антенн) для электромагнитных и акустических волн.

Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров. Одной из важных задач, возникающих при построении различных оптических и антенных устройств СВЧ–диапазона, является уменьшение потерь ( ) интенсивности света, мощности потока электромагнитной энергии при отражении от поверхностей линз, обтекателей антенн и пр. приборов, используемых для преобразований световых и радиоволн в разнообразных приборах фотоники, оптоэлектроники и радиоэлектроники.

Для уменьшения потерь на отражение используется покрытие оптических деталей (линз) 3 пленкой 2 со специальным образом подобранными толщиной δ и показателем преломления n (рис.7).

Рис.7 – Оптическая линза, пленка со специальным образом подобранными толщиной δ и показателем преломления n.

Значительно повысить коэффициент отражения R зеркал можно, используя последовательность чередующихся диэлектрических слоев с высоким и низким показателями преломления (рис.8).

Рис.8 – показатели преломления.

Дифракция света это отклонение световых лучей от прямолинейного распространения при прохождении сквозь узкие щели, малые отверстия или при огибании малых препятствий.
Явление дифракции света доказывает, что свет обладает волновыми свойствами.
Для наблюдения дифракции можно:
– пропустить свет от источника через очень малое отверстие или расположить экран на большом расстоянии от отверстия. Тогда на экране наблюдается сложная картина из светлых и темных концентрических колец.
– или направить свет на тонкую проволоку, тогда на экране будут наблюдаться светлые и темные полосы, а в случае белого света – радужная полоса.

Рис.9 – наблюдение дифракции света на малом отверстии.

3.1. Принцип Гюйгенса – Френеля.

Все вторичные источники, расположенные на поверхности фронта волны, когерентны между собой.
Амплитуда и фаза волны в любой точке пространства – это результат интерференции волн, излучаемых вторичными источниками.
Принцип Гюйгенса–Френеля дает объяснение явлению дифракции:
1. вторичные волны, исходя из точек одного и того же волнового фронта (волновой фронт – это множество точек, до которых дошло колебание в данный момент времени), когерентны, т.к. все точки фронта колеблются с одной и той же частотой и в одной и той же фазе;
2. вторичные волны, являясь когерентными, интерферируют.
Явление дифракции накладывает ограничения на применение законов геометрической оптики:
Закон прямолинейного распространения света, законы отражения и преломления света выполняются достаточно точно только, если размеры препятствий много больше длины световой волны.
Дифракция накладывает предел на разрешающую способность оптических приборов:
– в микроскопе при наблюдении очень мелких предметов изображение получается размытым
– в телескопе при наблюдении звезд вместо изображения точки получаем систему светлых и темных полос.

Зоны Френеля.

Френель решил задачу нахождения амплитуды в т. Р, заменив интегрирование суммированием, т.е. перешёл от непрерывных сумм ( ) к дискретным (Σ).

Рис.10–Зоны Френеля.

Точечный источник S создаёт сферическую волну. Требуется определить амплитуду колебаний волны в т. Р. Волновая поверхность в некоторой точке О будет представлять сферу. Френель предложил разбить ее на кольцевые зоны (секторы) так, что расстояния от краев каждой зоны до т. Р отличается на λ/2. Построенные таким образом сектора сферы называются зонами Френеля.

Волны, приходящие в т. Р от аналогичных точек двух соседних зон имеют противоположные фазы, т.к. разность хода между этими волнами равна λ/2.

При не слишком больших m (m – номер зоны), площади зон Френеля примерно равны S₁= S₂ =S_m. С ростом номера зоны m увеличивается расстояние b_m, от зоны до т. Р и угол φ между нормаль. к элементам зоны и направлением на т. Р. Тогда по формуле (1) амплитуда A_m колебания, возбуждаемого m зоной в т.Р, монотонно убывает.

3.3. Дифракция Фраунгофера на щели.

Физик И. Фраунгофер (1787–1826) рассмотрел дифракцию плюсках световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно точечный источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.

Рассмотрим дифракцию Фраунгофера от щели. Пусть плоская монохроматическая световая волна падает нормально плоскости узкой щели шириной а (рис.11). Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении j.

Разобьем открытую часть волновой поверхности в плоскости щели MN на зоны Френеля, имеющие вид полос, параллельных ребру М щели. Ширина каждой зоны выбирается так, чтобы разность хода от краев этих зон была равна l/2, т. е. всего на ширине щели уместится D:l/2 зон. Так как свет на щель падает нормально, то плоскость щели совпадает с волновым фронтом; следовательно, все точки волнового фронта в плоскости щели будут колебаться в одинаковой фазе. Амплитуды вторичных волн в плоскости щели будут равны, так как выбранные зоны Френеля имеют одинаковые площади и одинаково наклонены к направлению наблюдения.

Число зон Френеля, укладывающихся на ширине щели, зависит от угла j. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно гасят друг друга. Следовательно, если число зон Френеля четное, то и в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное, то и наблюдается дифракционный максимум, соответствующий действию одной не скомпенсированной зоны Френеля. Отметим, что в направлении j = 0щель действует как одна зона Френеля, и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В₀наблюдается центральный дифракционный максимум.

Рис.12 – Дифракция Фраунгофера на щели.

3.4. Дифракционная решетка.

Дифракционная решетка – это оптический прибор для измерения длины световой волны.
Дифракционная решетка представляет собой совокупность большого числа очень узких щелей, разделенных непрозрачными промежутками.
Если на решетку падает монохроматическая волна. то щели (вторичные источники) создают когерентные волны. За решеткой ставится собирающая линза, далее – экран. В результате интерференции света от различных щелей решетки на экране наблюдается система максимумов и минимумов.

Рис.13 – Дифракционная решетка.

Разность хода между волнами от краев соседних щелей равна длине отрезка АС. Если на этом отрезке укладывается целое число длин волн, то волны от всех щелей будут усиливать друг друга. При использовании белого света все максимумы (кроме центрального) имеют радужную окраску.

Чем больше штрихов нанесено на решетке, тем дальше друг от друга находятся дифракционные спектры и тем меньше ширина каждой линии на экране, поэтому максимумы видны в виде раздельных линий, т.е. разрешающая сила решетки увеличивается.
Точность измерения длины волны тем больше, чем больше штрихов приходится на единицу длины решетки.

Источник

Классические способы получения интерференционной картины от двух когерентных источников: щели Юнга, зеркала Френеля, бипризма Френеля.

Разделение первоначальной световой волны на две волны и последующее их сведение на экране – общий способ реализации всех двулучевых интерференционных схем. Такое разделение может быть выполнено с помощью экранов, щелей, зеркал и преломляющих тел.

Щели Юнга.

Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга источником света служит ярко освещенная щель S, от которойсветовая волна падает на две узкие равноудаленные щели S₁ и S₂, находящиеся на расстоянии d друг от друга (рис. 6.1.3). Таким образом, щели S₁ и S₂ играют роль когерентных источников, дающих две когерентные цилиндрические световые волны. Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников.

Рис. 6.1.3. Схема опыта Юнга

В области перекрытия световых пучков на экране (его центр – точка P) наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

Расстояние d между щелями S₁ и S₂ должно быть гораздо меньше расстояния L от щелей до экрана. Пусть расстояние между щелями d составляет 1 мм, а расстояние от щелей до экрана L = 1 м. Тогда для красного цвета (l = 600 нм) ширина интерференционной полосы Dх = 0,6 мм. В синем цвете ширина полосы Dх = 0,4 мм. По наблюдаемой ширине интерференционных полос Юнг впервые определил длины волн света, хотя его результаты были довольно неточными.

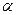
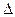
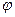
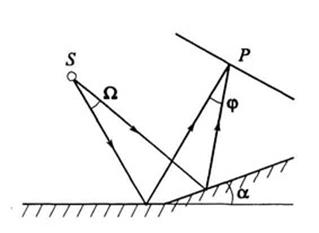
В опыте Френеля (1816 г.) свет от источника S отражается от двух зеркал (или бизеркала), расположенных под достаточно малым углом (рис. 6.1.4). Волны, падающие на экран, могут рассматриваться как волны от двух мнимых изображений источника S в обоих зеркалах. При изменении положения точки наблюдения P на экране изменяется разность хода , в результате чего возникает система интерференционных полос, ширина которых зависит от угла схождения лучей .

Рис. 6.1.4. Зеркала Френеля.

Бипризма Френеля.

Бипризма состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника (щели S) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые волны, как бы исходящие из мнимых когерентных источников S₁ и S₂ (рис. 6.1.5). На экране в области наложения волн наблюдается интерференционная картина в виде светлых и темных полос.

Рис. 6.1.5. Схема опыта с бипризмой Френеля

Условия образования максимума и минимума интенсивности света при интерференции двух волн. Ширина интерференционной полосы. Интерференционная картина от двух когерентных источников.

Рассмотрев общую схему получения интерференционной картины (рис. 6.1.2), мы получили формулу (6.1.7), дающую связь между разностью фаз δ и оптической разностью хода 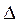двух интерферирующих волн.

Пусть в точке P накладываются две волны, и оптическая разность хода этих волн равна целому числу длин волн в вакууме:

, m = 0, 1, 2, …. (6.1.8)

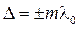
Тогда разность фаз таких волн оказывается кратной 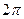и колебания, возбуждаемые в точке Робеими волнами, будут происходить с одинаковой фазой, то есть они будут усиливать друг друга. Поэтому (6.1.8) называется условием интерференционного максимума.

Если оптическая разность хода равна

, m =0, 1, 2,…, (6.1.9)

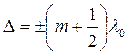
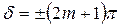
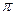
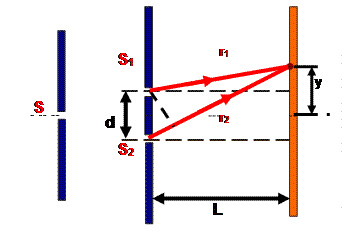
то разность фаз , то есть колебания находятся в противофазе (сдвинуты на ). В результате колебания, возбуждаемые в точке Робеими волнами, будут ослаблять (гасить) друг друга. Формула (6.1.9) называется условием интерференционного минимума.

Пусть точечные источники волн S₁ и S₂ расположены друг от друга на расстоянии d(рис. 6.1.6.). Колебания в точках S₁ и S₂ совершаются в одной фазе. Результат интерференции волн будем наблюдать на экране, расположенном от источников на расстояние L, большее по сравнению с расстоянием d.

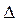
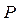
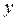
Определим разность хода , с которой приходят волны в точку экрана , отстоящую от его середины на расстояние .

Рис. 6.1.6. Расчет интерференционной картины от двух когерентных источников

Из рисунка видно, что , ,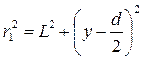

.

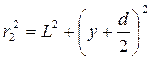
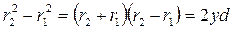
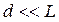
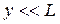
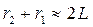
Мы полагаем, что и . При этих условиях можно считать .

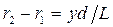
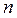
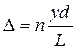
Тогда . Умножив эту разность на показатель преломления среды , получим оптическую разность хода .

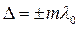
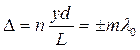
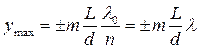
Определим, при каких значениях yбудут наблюдаться максимумы интенсивности. Условие наблюдения максимумов: . Следовательно: и

, m =0, 1, 2,…, (6.1.10)

где 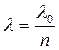— длина волны в среде, заполняющей пространство между источниками и экраном.

Для координат минимумов интенсивности получим:

, m =0, 1, 2,…. (6.1.11)

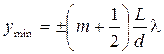
Расстояние между двумя соседними максимумамиинтенсивности называется расстоянием между интерференционными полосами.

Расстояние между соседними минимумами интенсивности называется шириной интерференционной полосы.

Из формул (6.1.10) и (6.1.11) для координат максимумов и минимумов видно, что расстояние между интерференционными полосами и ширина интерференционной полосы имеют одинаковое значение:

. (6.1.12)

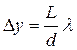
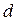
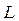
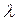
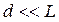
Согласно этой формуле расстояние между полосами при , сравнимом с , было бы того же порядка, что и , т.е. несколько микрон. В этом случае отдельные полосы были бы неразличимы. Вот почему для наблюдения интерференционной картины необходимо выполнение условия .

Источник