Способ получения когерентных волн зеркал френеля
| Методы наблюдения интерференции |   |
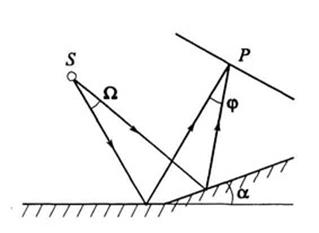
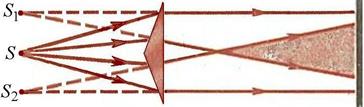
| Свет, испускаемый обычными источниками, можно рассматривать как хаотическую последовательность отдельных цугов синусоидальных волн. Длительность отдельного цуга не превышает 10 — 8 с даже в тех случаях, когда атомы источника не взаимодействуют (газоразрядные лампы низкого давления). Любой регистрирующий прибор имеет значительно большее время разрешения, поэтому наблюдение интерференции невозможно. Образование интерференционной картины можно наблюдать в рассмотренном нами в п. 8.2 опыте Юнга, использующем метод деления волнового фронта (рис. 8.3). Прошедший через узкую длинную щель S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя, параллельными между собой узкими щелями S1 и S2, расположенными близко друг к другу на равных расстояниях от S. Эти щели действуют как вторичные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Расстояние между соседними полосами равно: Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными. Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу (рис. 8.4). Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (рис. 8.5). Можно считать, что здесь образуются два близких мнимых изображения S1 и S2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть (рис. 8.6). Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щели Источник Классические способы получения интерференционной картины от двух когерентных источников: щели Юнга, зеркала Френеля, бипризма Френеля.
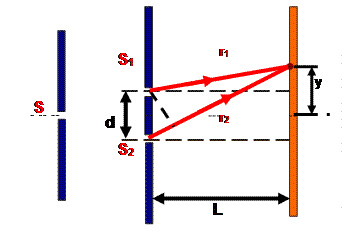
Разделение первоначальной световой волны на две волны и последующее их сведение на экране – общий способ реализации всех двулучевых интерференционных схем. Такое разделение может быть выполнено с помощью экранов, щелей, зеркал и преломляющих тел. Щели Юнга. Исторически первым интерференционным опытом, получившим объяснение на основе волновой теории света, явился опыт Юнга (1802 г.). В опыте Юнга источником света служит ярко освещенная щель S, от которойсветовая волна падает на две узкие равноудаленные щели S1 и S2, находящиеся на расстоянии d друг от друга (рис. 6.1.3). Таким образом, щели S1 и S2 играют роль когерентных источников, дающих две когерентные цилиндрические световые волны. Юнг был первым, кто понял, что нельзя наблюдать интерференцию при сложении волн от двух независимых источников. Рис. 6.1.3. Схема опыта Юнга В области перекрытия световых пучков на экране (его центр – точка P) наблюдалась интерференционная картина в виде чередующихся светлых и темных полос. Расстояние d между щелями S1 и S2 должно быть гораздо меньше расстояния L от щелей до экрана. Пусть расстояние между щелями d составляет 1 мм, а расстояние от щелей до экрана L = 1 м. Тогда для красного цвета (l = 600 нм) ширина интерференционной полосы Dх = 0,6 мм. В синем цвете ширина полосы Dх = 0,4 мм. По наблюдаемой ширине интерференционных полос Юнг впервые определил длины волн света, хотя его результаты были довольно неточными. В опыте Френеля (1816 г.) свет от источника S отражается от двух зеркал (или бизеркала), расположенных под достаточно малым углом Бипризма Френеля. Бипризма состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника (щели S) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые волны, как бы исходящие из мнимых когерентных источников S1 и S2 (рис. 6.1.5). На экране в области наложения волн наблюдается интерференционная картина в виде светлых и темных полос. Рис. 6.1.5. Схема опыта с бипризмой Френеля Условия образования максимума и минимума интенсивности света при интерференции двух волн. Ширина интерференционной полосы. Интерференционная картина от двух когерентных источников. Рассмотрев общую схему получения интерференционной картины (рис. 6.1.2), мы получили формулу (6.1.7), дающую связь между разностью фаз δ и оптической разностью хода Пусть в точке P накладываются две волны, и оптическая разность хода этих волн равна целому числу длин волн в вакууме: Тогда разность фаз таких волн оказывается кратной Если оптическая разность хода равна то разность фаз Пусть точечные источники волн S1 и S2 расположены друг от друга на расстоянии d(рис. 6.1.6.). Колебания в точках S1 и S2 совершаются в одной фазе. Результат интерференции волн будем наблюдать на экране, расположенном от источников на расстояние L, большее по сравнению с расстоянием d. Определим разность хода Рис. 6.1.6. Расчет интерференционной картины от двух когерентных источников Из рисунка видно, что Мы полагаем, что
Тогда Определим, при каких значениях yбудут наблюдаться максимумы интенсивности. Условие наблюдения максимумов: где Для координат минимумов интенсивности получим: Расстояние между двумя соседними максимумамиинтенсивности называется расстоянием между интерференционными полосами. Расстояние между соседними минимумами интенсивности называется шириной интерференционной полосы. Из формул (6.1.10) и (6.1.11) для координат максимумов и минимумов видно, что расстояние между интерференционными полосами и ширина интерференционной полосы имеют одинаковое значение: Согласно этой формуле расстояние между полосами при Источник |
.
. Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками 
и 
, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на 
, где 
— расстояние от S до ребра зеркал, b — расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно: 
. Поэтому ширина интерференционной полосы на экране равна:
.
.
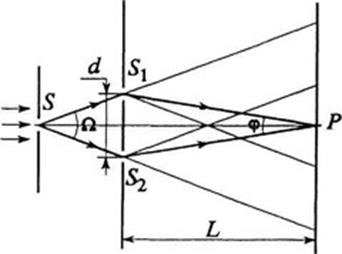
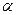(рис. 6.1.4). Волны, падающие на экран, могут рассматриваться как волны от двух мнимых изображений источника S в обоих зеркалах. При изменении положения точки наблюдения P на экране изменяется разность хода 
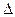, в результате чего возникает система интерференционных полос, ширина которых зависит от угла схождения лучей 
.
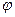двух интерферирующих волн.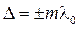
, m = 0, 1, 2, …. (6.1.8)
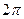и колебания, возбуждаемые в точке Робеими волнами, будут происходить с одинаковой фазой, то есть они будут усиливать друг друга. Поэтому (6.1.8) называется условием интерференционного максимума.
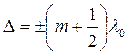, m =0, 1, 2,…, (6.1.9)
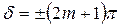, то есть колебания находятся в противофазе (сдвинуты на 
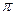). В результате колебания, возбуждаемые в точке Робеими волнами, будут ослаблять (гасить) друг друга. Формула (6.1.9) называется условием интерференционного минимума.
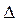, с которой приходят волны в точку экрана 
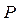, отстоящую от его середины на расстояние 
.
, 
,
.
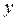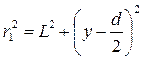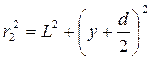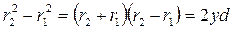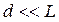и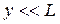 
. При этих условиях можно считать 
.
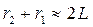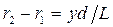. Умножив эту разность на показатель преломления среды 
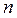, получим оптическую разность хода 
.
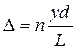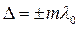. Следовательно: 
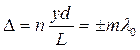и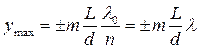
, m =0, 1, 2,…, (6.1.10)
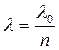— длина волны в среде, заполняющей пространство между источниками и экраном.
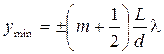, m =0, 1, 2,…. (6.1.11)
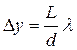. (6.1.12)
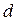, сравнимом с 
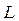, было бы того же порядка, что и 
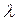, т.е. несколько микрон. В этом случае отдельные полосы были бы неразличимы. Вот почему для наблюдения интерференционной картины необходимо выполнение условия 
.
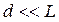