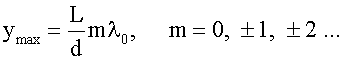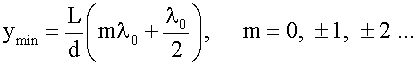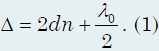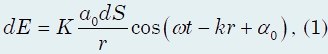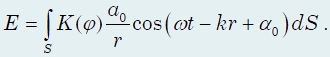Способ получения когерентных волн изображен

Содержание

Способы получения когерентных волн
Способ получения когерентных волн изображен
Методы получения когерентных волн
Способы получения когерентных волн.

Способы получения когерентных волн

Для получения когерентных волн необходимо взять один источник и идущую от него световую волну разделить на две части, которые затем заставить встретиться. Эти волны будут когерентны, т.к. будут принадлежать к одному и тому же моменту излучения, поэтому . .

Явления, используемые для разделения световой волны надвое.

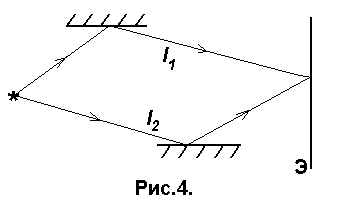
1. Явление отражения света (бизеркала Френеля). Рис.4.

2. Явление преломления света (бипризма Френеля). Рис.5.

3. Явление дифракции света.

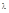
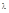
Это есть отклонение света от прямолинейного распространения при прохождении света через малые отверстия или вблизи непрозрачных препятствий, если их размеры (обоих) d соизмеримы с длиной волны (d

). То: Рис.6. – установка Юнга.

Во всех перечисленных случаях реальный источник света был точечным. В реальной жизни свет может быть протяженным – участок неба.

4. , n-показатель преломления пленки.

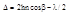
Возможны два случая:

— h=const, тогда 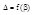. В этом случае интерференционная картина называется полоса равного наклона.

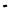
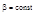
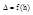
— h const. Падает параллельный пучок лучей. . -полосы равной толщины.

Установка «кольца Ньютона».

Надо рассматривать интерференционную картину в отраженном и преломленном свете.

Источник

Способ получения когерентных волн изображен

3.2. Методы получения когерентных волн

Для получения когерентных световых волн с помощью обычных (нелазерных) источников применяют метод разделения света от одного источника на две или нескольких систем волн (световых пучков). В каждой из них представлено излучение одних и тех же атомов источника, так что эти волны когерентны между собой и интерферируют при наложении.

Разделение света на когерентные пучки можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.

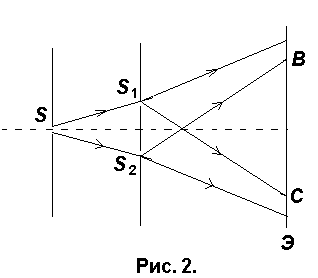
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S 1 и S 2 , параллельные щели S.

Таким образом, щели S 1 и S 2 играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.

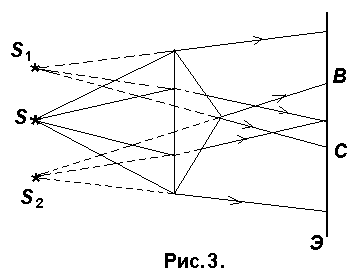
Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S 1 и S 2 , являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.

3.3. Оптическая длина пути и разность хода

Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l 1 и l 2 в средах с абсолютными показателями преломления n 1 и n 2 соответственно (рис.4).

Тогда фазы этих волн [см. (1) и (2.9)]

w t — j 1 = w t — k 1 l 1 + j 0 , w t — j 2 = w t — k 2 l 1 + j 0

j 2 — j 1 = k 2 l 2 — k 1 l 1 = 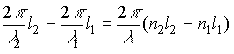(12)

где l 1 = l /n 1 , l 2 = l /n 2 -длины волн в средах, показатели преломления которых n 1 и n 2 соответственно, l — длина волны в вакууме.

Произведение геометрической длины пути l световой волны на абсолютный показатель преломления n называется оптической длиной пути волны.

Величину 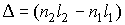(13)

называют оптической разностью хода интерферирующих волн. С учетом этого разность фаз

j 2 — j 1 = 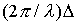(14)

Источник

Методы получения когерентных волн

Интерференция света. Оптическая разность хода. Методы получения когерентных световых волн.

Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

Оптическая разность хода — это разность оптических длин путей световых волн, имеющих общие начальную и конечную точки. В кристаллооптике разность хода обозначается R. По определению

В кристаллических анизотропных средах разность хода возникает из-за разных скоростей двух лучей в направлении, отличном от оптической оси.

Рассмотрим разность хода лучей, возникающую при прохождении света через зерно в шлифе.

На кристалл попадает пучок параллельных волн, перпендикулярных спилу. Поэтому угол падения равен нулю и отклонений по направлению не происходит. Поэтому выражение для R преобразуется в (d — толщина шлифа):

Так как для исследований важна максимальная интерференционная окраска, возникающая при максимальной разности хода, то это выражение переписывается в виде

В последнем выражении Δ — максимальное двулучепреломление.

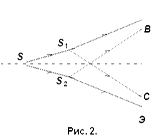Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S₁ и S₂, параллельные щели S. Таким образом, щели S₁ и S₂играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.

Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S₁ и S₂, являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.

3.3. Оптическая длина пути и разность хода

Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l₁и l₂ в средах с абсолютными показателями преломления n₁ и n₂ соответственно (рис.4). Тогда фазы этих волн [см. (1) и (2.9)] wt — j₁= wt — k₁l₁ + j₀ , wt -j₂= wt — k₂l₁ + j₀

j₂ -j₁ = k₂l₂ — k₁l₁ = 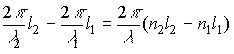(12)

где l₁= l/n₁, l₂= l/n₂ -длины волн в средах, показатели преломления которых n₁ и n₂соответственно, l — длина волны в вакууме.

Величину 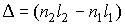(13)

называют оптической разностью хода интерферирующих волн. С учетом этого разность фаз

j₂ -j₁ = 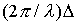(14)

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Способы получения когерентных волн.

Получение когерентных волн для реализации интерференции в оптике осуществляется двумя способами:

1.инструментальное получение из данного источника двух когерентных;

2.деление фронта волны.

Схемы получения когерентных волн в первом случае основаны на получении двух источников, которые являются двумя изображениями данного единого излучающего центра (метод Юнга, бипризма Френеля, зеркала Френеля). Во втором случае получение когерентных волн происходит делением волны в пределах цуга на две волны (интерферометр Майкельсона, тонкие пленки, клин, кольца Ньютона).

23. Интерференция. Условия максимума и минимума интерференции. Опыт Юнга.

Интерференция.

Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.

Условия максимума и минимума интерференции.

Опыт Юнга.

В этом опыте Юнг поток света направил на непрозрачную пластинку с двумя очень маленькими отверстиями, за которой находился экран. Если придерживаться господствовавшей в то время корпускулярной теории света, то на экране он должен был увидеть две светящиеся точки. Вместо этого на экране он увидел чередующиеся светлые и тёмные полосы. Причём самая яркая из них находилась на экране посередине между отверстиями на перегородке, чего быть вообще-то не должно. Юнг объяснил возникновение полос явлением интерференции света.

Но мы с вами ранее сказали, что интерференция — это сложение в пространстве двух или нескольких волн. Таким образом, мы, вслед за Юнгом, можем сказать, что свет обладает волновыми свойствами.

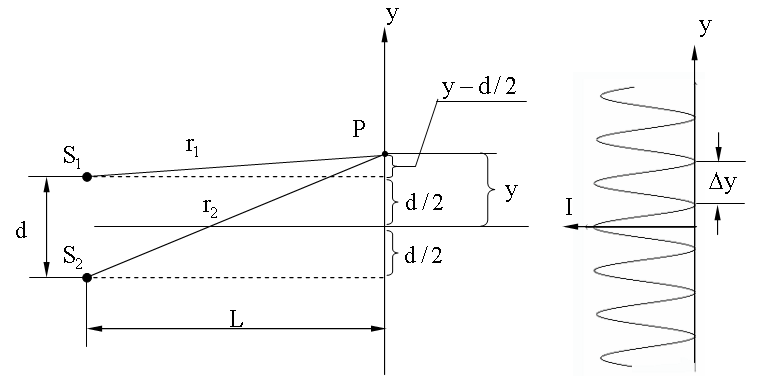
На экране светлые полосы соответствуют точкам, в которых фазы волн одинаковы, а тёмные — точкам, в которых фазы волн противоположны. Существует формула, по которой можно рассчитать, в каком месте экрана будет светлая, а в каком тёмная полоса:

Как видно из формул, расположение максимумов и минимумов на экране будет зависеть от расстояния между источниками (d), расстояния от источников до экрана (L) и от длины волны λ₀

24. Интерференция. Условия максимума и минимума интерференции. Кольца Ньютона.

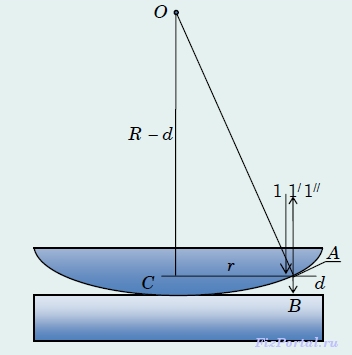
Кольца Ньютона.

Классическим примером полос равной толщины являются кольца Ньютона. Они наблюдаются при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки большой толщины и плоско-выпуклой линзы большого радиуса кривизны. Роль тонкой пленки, от которой отражаются когерентные волны, играет воздушный зазор между пластинкой и линзой. Падающий луч 1 отражается в точках А и В (рис.) от верхней и нижней поверхности воздушного клина и образует отраженные лучи 1 / и 1 // , имеющие разность хода:

25. Интерференция. Условия максимума и минимума интерференции. Плоскопараллельная пластинка.

Плоскопараллельная пластина.

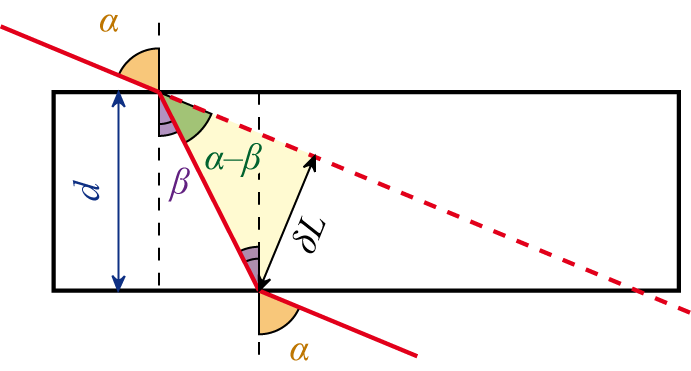
Плоскопараллельная пластина — это оптический прибор, представляющий собой ограниченный параллельными поверхностями слой однородной среды, прозрачной в некотором интервале длин волн λ оптического излучения. Основным оптическим свойством пластины является то, что луч, падающий на пластину, в результате двукратного преломления на поверхностях пластины параллельно смещается на некоторую величину δL относительно исходного луча (см. рисунок).

Плоскопараллельную пластину можно рассматривать в качестве сферической линзы, ограниченной поверхностями бесконечного радиуса. Для такой линзы величина оптической силы равна нулю. Именно поэтому обычные оконные стекла не искажают изображения, а лишь немного смещают его. Но такой сдвиг незаметен глазу, поскольку сдвигается все изображения в поле зрения.

26. Интерференция. Условия максимума и минимума интерференции. Тонкий клин.

27. Дифракция. Виды дифракции. Принцип Гюйгенса-Френеля.

Дифракция.

Под дифракцией света понимают явление непрямолинейного распространения света, проникновение его в область геометрической тени, огибание им препятствий.

Виды дифракции.

1. Дифракция на круглом отверстии (дифракция Френеля).

2. Дифракция от щели (дифракция Фраунгофера).

3. Дифракционная решётка.

Принцип Гюйгенса-Френеля.

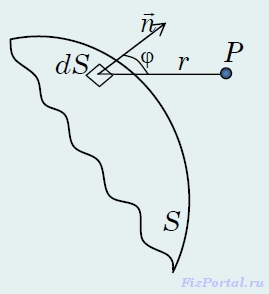
Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S (рис.) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS.

Амплитуда этой вторичной волны убывает с расстоянием r от источника вторичной волны до точки наблюдения по закону 1/r. Следовательно, от каждого участка dS волновой поверхности в точку наблюдения Р приходит элементарное колебание:

где (ωt + α0)− фаза колебания в месте расположения волновой поверхности S, k− волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а₀ определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0этот коэффициент максимален, а при φ/2он равен нулю.

Результирующее колебание в точке Р представляет собой суперпозицию колебаний (1), взятых для всей поверхности S:

Эта формула является аналитическим выражением принципа Гюйгенса-Френеля.

28. Метод зон Френеля (на примере сферической волны). Условия дифракционного максимума и минимума. Дифракция на малом отверстии.

Метод зон Френеля (на примере сферической волны).

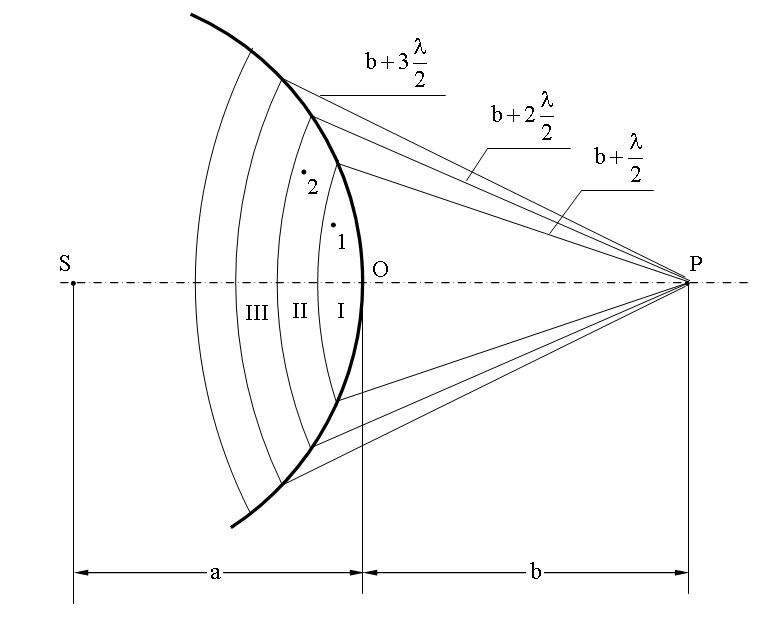
Френель предложил метод разбиения фронта волны на кольцевые зоны, который впоследствии получил название метод зон Френеля.

Пусть от источника света S распространяется монохроматическая сферическая волна, P — точка наблюдения. Через точку O проходит сферическая волновая поверхность. Она симметрична относительно прямой SP.

Разобьем эту поверхность на кольцевые зоны I, II, III и т.д. так, чтобы расстояния от краев зоны до точки P отличались на l/2 — половину длины световой волны. Это разбиение было предложено O. Френелем и зоны называют зонами Френеля.

Возьмем произвольную точку 1 в первой зоне Френеля. В зоне II найдется, в силу правила построения зон, такая соответствующая ей точка, что разность хода лучей, идущих в точку P от точек 1 и 2 будет равна l/2. Вследствие этого колебания от точек 1 и 2 погасят друг друга в точке P.

Из геометрических соображениях следует, что при не очень больших номерах зон их площади примерно одинаковы. Значит каждой точке первой зоны найдется соответствующая ей точка во второй, колебания которых погасят друг друга. Амплитуда результирующего колебания, приходящего в точку P от зоны с номером m, уменьшается с ростом m, т.е.

Последнее изменение этой страницы: 2017-03-14; Просмотров: 3408; Нарушение авторского права страницы

Источник