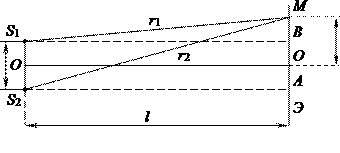Способ получения когерентных волн бипризма френеля
| Методы наблюдения интерференции |   |
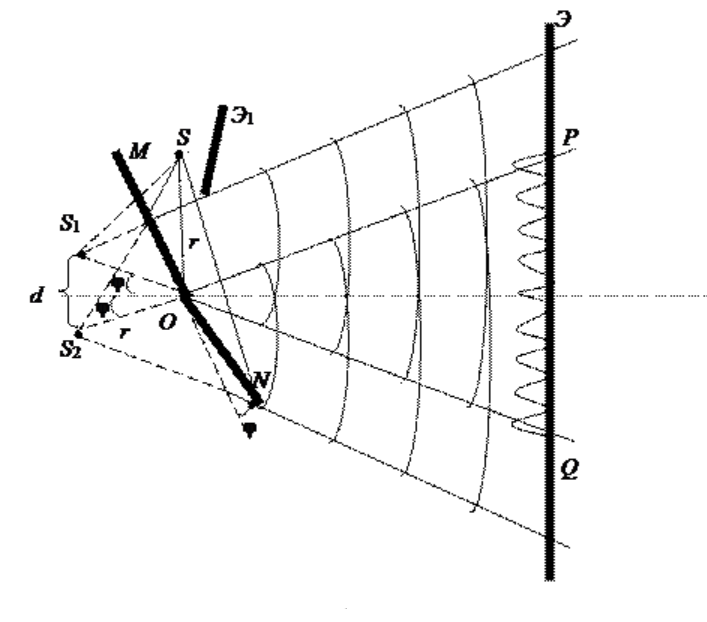
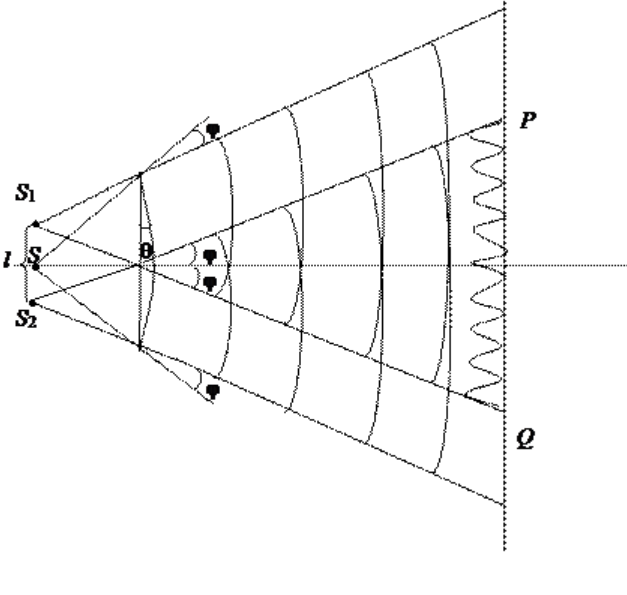
| Свет, испускаемый обычными источниками, можно рассматривать как хаотическую последовательность отдельных цугов синусоидальных волн. Длительность отдельного цуга не превышает 10 — 8 с даже в тех случаях, когда атомы источника не взаимодействуют (газоразрядные лампы низкого давления). Любой регистрирующий прибор имеет значительно большее время разрешения, поэтому наблюдение интерференции невозможно. Образование интерференционной картины можно наблюдать в рассмотренном нами в п. 8.2 опыте Юнга, использующем метод деления волнового фронта (рис. 8.3). Прошедший через узкую длинную щель S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран B с двумя, параллельными между собой узкими щелями S1 и S2, расположенными близко друг к другу на равных расстояниях от S. Эти щели действуют как вторичные синфазные источники, и исходящие от них волны, перекрываясь, создают интерференционную картину, наблюдаемую на удаленном экране C. Расстояние между соседними полосами равно: Измеряя ширину интерференционных полос, Юнг в 1802 г. впервые определил длины световых волн для разных цветов, хотя эти измерения и не были точными. Другой интерференционный опыт, аналогичный опыту Юнга, но в меньшей степени осложненный явлениями дифракции и более светосильный, был осуществлен О. Френелем в 1816 г. Две когерентные световые волны получаются в результате отражения от двух зеркал М и N, плоскости которых наклонены под небольшим углом φ друг к другу (рис. 8.4). Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы (рис. 8.5). Можно считать, что здесь образуются два близких мнимых изображения S1 и S2 источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть (рис. 8.6). Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щели Источник Основные интерференционные схемыДля интерференции света необходимым условием является получение когерентных световых пучков. В процессе его выполнения, свое применение находят различные приемы. До того времени, когда во всех приборах для наблюдения интерференции света появились лазеры, когерентные пучки получали с помощью разделения и последующего сведения световых лучей, испускаемым одним и тем же источником. На практике, это может быть осуществимо при помощи экранов и щелей, зеркал и преломляющих тел. Разберем некоторые из таких методов.
Метод Юнга и интерференция светаПервое наблюдение явления интерференции световых волн, а также и определение их длин были совершены Т. Юнгом. Роль источника света играет ярко освещенная щель S (рисунок 1 ), из которой световая волна попадает на две параллельные щели S , узкие равноудаленные щели S 1 и S 2 . Исходя из этого, можно сделать вывод, что щели S 1 и S 2 в данной ситуации являются когерентными источниками. Интерференционная картина (область ВС) наблюдается на экране Э , установленном на определенном расстоянии параллельно S 1 и S 2 . Зеркала ФренеляПара плоских соприкасающихся зеркал О М и O N расположены таким образом, что угол между их отражающими поверхностями, крайне близок к нулю (рис. 2 ). По этой причине угол j на изображении очень мал. Параллельно линии пересечения зеркал О , на некотором расстоянии r от нее, размещается прямолинейный источник света S , такой как, к примеру, узкая светящаяся щель. Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников S 1 и S 2 . Путь света от источника S к экрану Э преграждает непрозрачный экран Э 1 .
Луч O Q является отражением луча S O от зеркала О М , луч О Р , в свою очередь, представляет собой отражение луча S O от зеркала O N . Несложно понять, что угол между лучами О Р и O Q эквивалентен 2 j . По той причине, что S 1 и S 2 располагаются относительно О М симметрично, длина отрезка O S 1 равняется длине O S , другими словами r . Подобные рассуждения становятся результатом получения того же результата для отрезка O S 2 . Исходя из вышесказанного, можно заявить, что расстояние между источниками S 1 и S 2 равно d = 2 r sin ( j ) ≫ 2 p j . Бипризма ФренеляПара изготовленных из одного куска стекла призм с мизерным преломляющим углом q обладают одной общей гранью и называются бипризмой Френеля (рис. 3 ).
Параллельно данной грани на некотором расстоянии a от нее, находится прямолинейный источник света S . При условии, если преломляющий угол q призмы пренебрежительно мал, а углы падения лучей на грань призмы не сильно велики, то каждый луч отклоняется призмой на почти один и тот же угол, эквивалентный j = ( n — l ) q , где n представляет собой показатель преломления призмы. В случае, когда угол падения лучей на бипризму небольшой, все лучи отклоняются каждой из половин бипризмы на аналогичные углы. Как результат, появляется пара когерентных цилиндрических волн, испускаемых из мнимых источников S 1 и S 2 и принадлежащих той же плоскости, что и S . Интерференция проявляется в качестве результата наложения двух расходящихся пучков света, расходящихся от двух когерентных источников, располагающихся на некотором расстоянии l от экрана Э , как это проиллюстрировано на рисунке 1 . По данной причине порядок расчета и результат наложения волн будут абсолютно равны. Область, в которой волны накладываются друг на друга, носит название поля интерференции. Во всей этой области наблюдается чередование мест с максимальной и минимальной интенсивностью света. Если в поле интерференции поместить экран, то на нем будет проявляться интерференционная картина, выражающаяся в виде чередования светлых и темных полос.
Пускай когерентные источники S 1 и S 2 расположены на некотором расстоянии d друг от друга, а экран Э вместе источниками находится в некой среде с абсолютным показателем преломления n . Определим оптическую разность хода между когерентными волнами, распространяющимися от источников S 1 и S 2 в приведенную точку M на экране. Точка M размещена на расстоянии x от центра интерференционной картины. ∆ = L 2 — L 1 = r 2 n — r 1 n = n ( r 2 — r 1 ) , где L 2 = r 2 n и L 1 = r 1 n представляют собой оптические длины пути для первой и второй волн, а r 2 и r 1 – геометрические длины пути первой и второй волн. Для случая треугольников S 1 А М и S 2 В М будет справедливой следующая запись: r 2 2 = l 2 + x + d 2 2 , r 1 2 = l 2 + x — d 2 2 ⇒ r 2 2 — r 1 2 = x + d 2 2 — x — d 2 2 ⇒ r 2 — r 1 r 2 + r 1 = 2 x d . Так как, l ≫ d , можно заключить, что r 2 + r 1 ≈ 2 l , учитывая это, выражаем: r 2 — r 1 r 2 + r 1 = 2 x d ⇒ r 2 — r 1 2 l = 2 x d ⇒ r 2 — r 1 = x d l . Оптическая разность ход будет эквивалентна выражению: ∆ = n ( r 2 — r 1 ) = n x d l . Применяя условие интерференционных максимумов для оптической разности хода двух волн в формулу ∆ = n r 2 — r 1 = n x d l , выведем координаты максимумов, другими словами, положение светлых полос, на экране n x m a x d l = 2 m λ 2 и x m a x = m λ l m d , m = 0 , 1 , 2 , 3 . . . . В точке x m a x = 0 размещается максимум, соответствующий нулевой оптической разности хода. Порядок интерференции для такого максимума m = 0 . Он является центром интерференционной картины. Подставляя условие интерференционных минимумов для оптической разности хода двух волн в приведенное выражение ∆ = n r 2 — r 1 = n x d l , определим положение темных полос на экране или же координаты минимумов: n x m i n d l = 2 m + 1 λ 2 и x m i n = 2 m + 1 λ l 2 n d , m = 0 , 1 , 2 , 3 . . . Расстояние между двумя соседними максимумами (или минимумами), порядок m которых отличается на единицу, определяется как ширина интерференционной полосы. ∆ x = x m — x m — 1 = m λ l n d — ( m — 1 ) λ l n d = λ l n d . Источник |
.
. Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками 
и 
, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на 
, где 
— расстояние от S до ребра зеркал, b — расстояние от ребра до экрана (см. рис 8.4.). Расстояние d между вторичными источниками равно: 
. Поэтому ширина интерференционной полосы на экране равна:
.
.
