Способ получения когерентных световых волн

3.2. Методы получения когерентных волн

Для получения когерентных световых волн с помощью обычных (нелазерных) источников применяют метод разделения света от одного источника на две или нескольких систем волн (световых пучков). В каждой из них представлено излучение одних и тех же атомов источника, так что эти волны когерентны между собой и интерферируют при наложении.

Разделение света на когерентные пучки можно осуществить с помощью экранов и щелей, зеркал и преломляющих тел. Рассмотрим некоторые из этих методов.

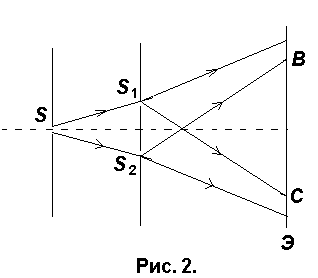
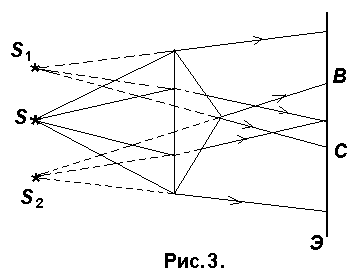
Источником света служит ярко освещенная щель S, от которой световая волна падает на две узкие щели S 1 и S 2 , параллельные щели S.

Таким образом, щели S 1 и S 2 играют роль когерентных источников. На экране Э (область ВС) наблюдается интерференционная картина в виде чередующихся светлых и темных полос.

Она состоит из двух одинаковых сложенных основаниями призм. Свет от источника S преломляется в обеих призмах, в результате чего за призмой распространяются лучи, как бы исходящие от мнимых источников S 1 и S 2 , являющихся когерентными. Таким образом, на экране Э (область ВС) наблюдается интерференционная картина.

3.3. Оптическая длина пути и разность хода

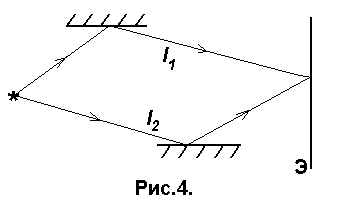
Пусть две когерентные волны (см. 3.1) создаются одним источником S, но до экрана проходят разные геометрические длины путей l 1 и l 2 в средах с абсолютными показателями преломления n 1 и n 2 соответственно (рис.4).

Тогда фазы этих волн [см. (1) и (2.9)]

w t — j 1 = w t — k 1 l 1 + j 0 , w t — j 2 = w t — k 2 l 1 + j 0

j 2 — j 1 = k 2 l 2 — k 1 l 1 = 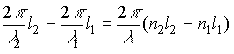(12)

где l 1 = l /n 1 , l 2 = l /n 2 -длины волн в средах, показатели преломления которых n 1 и n 2 соответственно, l — длина волны в вакууме.

Произведение геометрической длины пути l световой волны на абсолютный показатель преломления n называется оптической длиной пути волны.

Величину 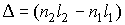(13)

называют оптической разностью хода интерферирующих волн. С учетом этого разность фаз

j 2 — j 1 = 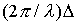(14)

Источник

2.3. Способы получения когерентных волн

Очевидно, что получить когерентные волны от двух независимых источников света практически невозможно. Это связано с тем, что свет атомом излучается в процессе перехода электронов атома с одного энергетического уровня на другой. Момент такого перехода носит вероятностный характер, соответственно, случайна фаза излучаемой атомом электромагнитной волны. Излучение источника складывается из совокупности излучений отдельных атомов и фаза его, естественно, меняется случайным образом. Следовательно, независимые источники излучают световые волны, разность фаз которых меняется хаотично.

Когерентные волны можно получить, если излучение одного источника разделить на два пучка, заставить каждый пучок пройти разные оптические пути, а затем наложить их друг на друга. В этом случае фазы световых волн в каждом пучке меняются хаотично, но синхронно друг с другом, т.е. разность фаз остается постоянной, и пучки будут когерентными. Такое разделение можно осуществить двумя способами — делением волнового фронта и делением амплитуды волны. Способы деления амплитуды волны будут рассмотрены далее, а в данном пункте рассмотрим несколько конкретных интерференционных схем, в которых используется метод деления световой волны по фронту.

Схема Юнга. Пучок света падает на непрозрачный экран с узкой щелью (рис.2.3). Прошедшим светом освещаются две узкие параллельные щели во втором непрозрачном экране. На этих щелях свет испытывает дифракцию, в результате чего за щелями получаются два расходящихся световых пучка. Эти пучки когерентные, т.к. исходят от одного источника. В области их перекрытия АВ наблюдается интерференционная картина.

Бизеркала Френеля. Два плоских соприкасающихся зеркала (рис.1.2) установлены так, что угол между их плоскостями близок к 180 О . Зеркала освещаются светом от источника S (как правило, в качестве источника берется узкая светящаяся щель, ориентированная параллельно линии соединения зеркал). При отражении от зеркал падающий свет разделяется на две когерентные цилиндрические волны, распространяющиеся так, как если бы они исходили из мнимых источников S₁ и S₂, являющихся изображением источника в каждом из зеркал. На экране, где волны перекрываются, наблюдается интерференционная картина.

Бипризма Френеля. Бипризма Френеля (рис.2.5) состоит из двух призм с небольшими преломляющими углами , склеенных по малым основаниям. Параллельно основаниям призм на оси симметрии системы располагается узкая светящаяся щель . После преломления в каждой из призм лучи отклоняются от своего первоначального пути на угол =(n-1), где n— показатель преломления стекла, из которого изготовлены призмы. После преломления в бипризме падающий от S пучок света разделяется на два, как бы исходящих из мнимых источников S₁ и S₂, находящихся в точках пересечения продолжений преломленных лучей. На экране в области пересечения преломленных пучков АВ наблюдается интерференционная картина.

Билинза Бийе. а) Тонкая сферическая линза разрезается по диаметру, и ее половинки разводятся на небольшое расстояние. Образовавшийся промежуток между половинками линзы закрывается непрозрачным экраном. Источник света S помещается на оси симметрии системы на двойном фокусном расстоянии от линзы. В результате получают два действительных изображения S₁ и S₂ точечного источника S (рис.2.5). S₁ и S₂ являются источниками сферических когерентных волн. В области их перекрытия наблюдается интерференционная картина.

б) Из тонкой линзы вырезается по диаметру узкая полоска, а оставшиеся части склеиваются по срезу. Источник света помещается в фокусе линзы. В результате преломления лучей в половинках линзы получаем два пучка с плоскими фронтами, распространяющимися под малым углом друг к другу. В области перекрытия пучков наблюдается интерференционная картина (см. рис.2.6).

Во всех (кроме последнего) рассмотренных выше способах получения когерентных волн расчет параметров интерференционной картины сводится к уже изученному нами случаю двух когерентных источников (п.2.2). Надо только в формуле (2.14) использовать расстояние между источниками S₁ и S₂ и расстояние от источников до экрана, найденные с учетом особенностей геометрии каждого конкретного случая.

Источник

ВОЛНОВАЯ ОПТИКА

18.2. Способы получения когерентных источников

Когерентные источники получают, разделив световую волну, идущую от одного источника на две.

18.2.1. Опыт Юнга

Томас Юнг наблюдал интерференцию от двух источников, прокалывая на малом расстоянии (d ≈ 1мм) два маленьких отверстия в непрозрачном экране. Отверстия освещались светом от солнца, прошедшим через малое отверстие в другом непрозрачном экране.

Интерференционная картина наблюдалась на экране, удаленном на расстоянии L ≈ 1м от двух источников. Так, впервые в истории, Т. Юнг определил длины световых волн.

При использовании лазера в качестве источника света необходимость в экране отпадает.

18.2.2. Зеркала Френеля

Свет от узкой щели S падает на два плоских зеркала, развернутых друг относительно друга на очень малый угол φ . Используя закон отражения света (17.1.3.) нетрудно показать, что падающий пучок света разобьется на два, исходящих из мнимых источников S₁ и S₂ . Источник S закрывают от экрана наблюдения непрозрачным экраном.

18.2.3. Бипризма Френеля

Две стеклянные призмы с малым преломляющим углом θ изготавливают из одного куска стекла так, что призмы сложены своими основаниями, Источник света — ярко освещенная щель S . После преломления в бипризме падающий пучок расщепляется на два, исходящих от мнимых источников S₁ и S₂ , которые дают две когерентные цилиндрические волны.

Так как преломляющий угол θ мал, то все лучи отклоняются каждой из половинок бипризмы на один и тот же угол φ . Можно показать, что в этом случае

здесь n — показатель преломления материала призмы.

Расстояние между источниками:

18.2.4. Интерференция при отражении от прозрачных пластинок

Луч света, падающий на прозрачную пластинку, частично отражается и частично преломляется. Преломленный луч, отражаясь от нижней поверхности пластинки, идет к верхней и преломляется на ней второй раз. Таким образом получаются два луча.

Если источник света естественный, то необходимым условием когерентности является малая толщина пластинок (интерференция в тонких пленках). При освещении лазерным лучом это ограничение отпадает.

При определении оптической разности хода необходимо учитывать изменение фазы отраженной волны на противоположную, если отражение происходит от оптически более плотной среды.

Здесь λ₀/2 появилась за счет изменения фазы волны на противоположную при отражении в точке A . Связь разности фаз δ и разности хода Δ , см. (18.1.2.2.).

18.2.4.1. Кольца Ньютона

Плосковыпуклая линза большого радиуса кладется на стеклянную пластинку и освещается сверху параллельным пучком света. Так как радиус линзы R велик по сравнению с r — радиусом интерференционных полос, то угол падения света на внутреннюю поверхность линзы i ≈ 0 . Тогда геометрическая разность хода с большой точностью равна 2b . При нахождении оптической разности хода следует учитывать изменение фазы на противоположную при отражении от оптически более плотной среды. Связь между b, r и R нетрудно найти из геометрических соображений.

Если в зазоре между линзой и пластиной n = 1 , то для радиуса интерференционных полос (колец Ньютона) получается формула:

При четном m кольца Ньютона темные, в частности при m = 0, r = 0 и в центре наблюдается темное пятно (из-за потери λ₀/2 при отражении от стеклянной пластинки).

Если m нечетное, то кольца светлые.

18.3. Многолучевая интерференция

Пусть в заданную точку экрана посылают световые волны N источников одинаковой интенсивности ( N > 2 ).

Предположим, что колебание, возбуждаемое каждым последующим источником сдвинуто по фазе относительно предыдущего на δ . Результирующую амплитуду A можно выразить через A₀ — амплитуду от одного источника, используя метод векторной диаграммы (14.3.1, 14.3.2).

Выразим A и A₀ через вспомогательный параметр R — радиус окружности, на которой лежат начала и концы наших векторов:

После исключения R получим амплитуду результирующего колебания:

Если δ = 0 (все колебания имеют одинаковую фазу) полученное выражение становится неопределенным. Взяв производную по δ от числителя и знаменателя, найдем по правилу Лопиталя, что при δ = 0 амплитуда результирующего колебания:

Этот результат непосредственно очевиден из векторной диаграммы, построенной для случая δ = 0 , т.к. все векторы будут направлены вдоль одной прямой. Интенсивность света (16.5.4) I

Источник