Способ получения когерентных пучков делением волнового фронта

Перечислите способы получения когерентных световых пучков. Как образуются когерентные пучки света при наблюдении колец Ньютона?

В чем заключается явление интерференции света? При каких условиях оно наблюдается?

Интерфере́нция све́та — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких когерентных световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной.

В природе часто можно наблюдать радужное окрашивание тонких пленок (масляные пленки на воде, мыльные пузыри, оксидные пленки на металлах), возникающее в результате интерференции света, отраженного двумя поверхностями пленки.

Условие когерентности световых волн

Причина состоит в том, что световые волны, излучаемые различными источниками, не согласованы друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные волны. Они должны иметь одинаковые длины волн и постоянную разность фаз в любой точке пространства. Напомним, что такие согласованные волны с одинаковыми длинами волн и постоянной разностью фаз называются когерентными.

Почти точного равенства длин волн от двух источников добиться нетрудно. Для этого достаточно использовать хорошие светофильтры, пропускающие свет в очень узком интервале длин волн. Но невозможно осуществить постоянство разности фаз от двух независимых источников. Атомы источников излучают свет независимо друг от друга отдельными «обрывками» (цугами) синусоидальных волн, имеющими длину около метра. И такие цуги волн от обоих источников налагаются друг на друга. В результате амплитуда колебаний в любой точке пространства хаотически меняется со временем в зависимости от того, как в данный момент времени цуги волн от различных источников сдвинуты друг относительно друга по фазе. Волны от различных источников света некогерентны из-за того, что разность фаз волн не остается постоянной (исключение составляют квантовые источники света – лазеры, созданные в 1960 г.). Никакой устойчивой картины с определенным распределением максимумов и минимумов освещенности в пространстве не наблюдается.

Наиб, широко известна И. с., характеризующаяся образованием стационарной (постоянной во времени) интерференционной картины (и. к.) — регулярного чередования в пространстве областей повыш. и пониж. интенсивности света, получающейся в результате наложения когерентных световых пучков, т. е. в условиях постоянной (или регулярно меняющейся) разности фаз. Реже и только в спец. условиях эксперимента наблюдаются явления нестационарной И. с., к к-рым относятся световые биения и эффекты корреляции интенсивностей. Строгое объяснение явлений нестационарной И. с. требует учёта как волновых, так и корпускулярных свойств света и даётся на основе квантовой электродинамики. Стационарная И. с. возникает при наличии когерентности (определ. корреляции фаз) налагающихся волн. Взаимно когерентные световые пучки могут быть получены путём разделения и последующего сведения лучей, исходящих от общего источника света. При этом требование когерентности налагает нек-рые ограничения на угл. размеры источника и на ширину спектра излучения.

Какие источники света называются когерентными?

— взаимная согласованность протекания во времени световых колебаний в разных точках пространства и (или) времени, характеризующая их способность к интерференции. В общем случае световые колебания частично когерентны и количественно их когерентность измеряется степенью взаимной когерентно с-т и (с. в. к.), к-рая определяет контраст интерференционной картины (и. к.) в том или ином интерференц. эксперименте.

Когерентные источники света – это источники, которые имеют постоянную во времени разность фаз, согласованное протекание нескольких колебательных или волновых процессов, степень которых различна.

Перечислите способы получения когерентных световых пучков. Как образуются когерентные пучки света при наблюдении колец Ньютона?

Интерферировать могут только когерентные волны. Источники называют когерентными, если они имеют одинаковую частоту и постоянную во времени разность фаз излучаемых ими волн.

Когерентными могут быть только точечные монохроматические источники. К ним по свойствам близки лазеры. Обычные источники излучения некогерентны, так как немонохроматичны и не являются точечными.

Немонохроматичность излучения обычных источников обусловлена тем, что их излучение создается атомами, испускающими в течение времени порядка =108 с волновые цуги длиной L=c=3 м. Излучения разных атомов не коррелированы друг с другом.

Однако наблюдать интерференцию волн можно и при использовании обычных источников, если с помощью какого-либо приема создать два или более источников, подобных первичному источнику. Существует два метода получения когерентных световых пучков или волн: метод деления волнового фронта и метод деления амплитуды волны. В методе деления волнового фронта пучок или волна делится, проходя через близко расположенные щели или отверстия (дифракционная решетка), либо с помощью отражающих и преломляющих препятствий (бизеркало и бипризма Френеля, отражательная дифракционная решетка).

В методе деления амплитуды волны излучение делится на одной или нескольких частично отражающих, частично пропускающих поверхностях. Примером является интерференция лучей, отраженных от тонкой пленки.

Источник

Получение когерентных пучков делением волнового фронта

Для наблюдения интерференции света от реальных (некогерентных) источников необходимо свет от одного и того же источника разделить на два пучка (или несколько пучков) и затем свести эти пучки вместе.

Способов разделения волны от первичного источника на две когерентные между собой волны два: деление волнового фронта (метод Юнга, зеркала Френеля и др.) и деление амплитуды (интерференция в тонких пленках).

Метод получения когерентных пучков делением волнового фронта (он пригоден только для достаточно малых источников) заключается в том, что исходящий из источника пучок делится на два (например, проходя через два близкорасположенных отверстия), а при наложении их друг на друга разность хода между интерферирующими лучами должна быть меньше длины когерентности.

Роль вторичных когерентных источников и играют две узкие щели, освещаемые одним источником малого углового размера, а в более поздних опытах свет пропускался через узкую щель , равноудаленную от двух других щелей. Интерференционная картина наблюдается в области перекрытия световых пучков, исходящих из и .

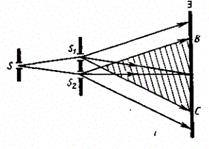
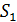
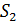
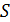
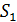
Рис. 2.2.1 Опыт Юнга

Свет от источника S падает расходящимся пучком на два плоских зеркала, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол мал). Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S1 и S2, которые действуют как когерентные источники.

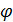
Интерференционная картина наблюдается в области взаимного перекрытия отраженных пучков.

Рис.2.2.2 Зеркала Френеля

Бипризма Френеля

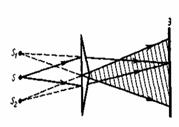
Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S1 и S2, являющихся когерентными.

Источник

Когерентность. Способы получения когерентных пучков

В повседневной жизни явление интерференции не наблюдается (светлые и темные полосы). Что же такое когерентность?

Когерентность – согласованное протекание нескольких колебательных процессов.

Характеристики волны: амплитуда, частота и фаза. У когерентных волн разность фаз постоянна (см. выше). Эти характеристики для таких волн могут быть или изменяемы или постоянны. Но с изменением равным константе.

Все зависит от времени. Величина меняется хаотически. При рассмотрении интенсивности света мы (***) среднем определяем промежуток времени.

Для наблюдения интерференции необходимы когерентные источники. Какие есть способы получения когерентных источников?

— синусоидальная волна абсолютная математическая абстракция.

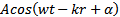
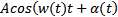
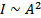
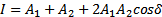
(w — круговая частота, k – волновой вектор, х – координата (т.к. свет можно рассматривать в одномерном пространстве); k = w/v). В реальности атомы излучают несколько кусочков синусоиды и согласно принципу неопределенности, каждый атом излучает эту частичку в неком диапазоне частот: . — интенсивность света пропорциональна квадрату амплитуды. .

Если бы наш глаз мог регистрировать картинки с временным разрешением 10 -10 , то у нас рябило бы в глазах. Глаз усредняет картинку 0,1 с. Физический прибор имеет время регистрации дельта t. Если за 0,1 с 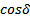пробегает все значения от -1 до 1 и не один раз, то при усреднении получится 0. Помимо того, что этот cos принимает разные значения, есть еще и разные значения волн.

Время когерентности – время за которое изменение достигает пи.

Длина когерентности — .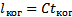

На этих знаниях основаны способы получения когерентных пучков:

1. Метод деления волнового фронта основан на использовании двух экранов. Как поставить линзу и источник, чтобы получился луч падающий на экран. Дельта х должно быть меньше длины когерентности.

2. Метод деления амплитуды основан на отражении света в мелкой пластинке. Исходная волна 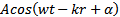разделилась амплитуда и снова деления многочисленные.

Источник

Получение интерференционных картин делением волнового фронта (метод Юнга) и делением амплитуды (метод Френеля)

Вы будете перенаправлены на Автор24

Способов получения волн способных интерферировать в оптике всего два:

деление амплитуды волны,

деление фронта волны.

Метод Юнга

Для получения интерференции методом деления волнового фронта когерентные волны получают как два участка одного фронта волны.

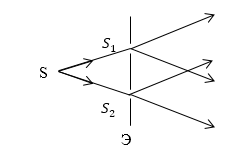
Первым, кто сконструировал установку для демонстрации явления интерференции световых волн, был Т. Юнг. При этом он использовал именно метод деления волнового фронта. Яркий пучок солнечного света попадал на экран с малым отверстием или узкой щелью. Получался как бы свет от точечного, монохроматического источника света ($S$). После дифракции на щели световая волна распространялась до двух маленьких отверстий ($S_1\ и\ S_2$), сделанных в экране ($Э$) рис.1. После очередной дифракции два расходящихся пучка света перекрывали друг друга, и так как являлись когерентными, при наложении давали интерференционную картину. При этом расстояния:

Данные отверстия работают как вторичные монохроматические, точечные источники. Световые пучки вторичных источников перекрываются за экраном $Э$ (рис.1). Картина интерференции наблюдается в области перекрывания данных световых пучков.

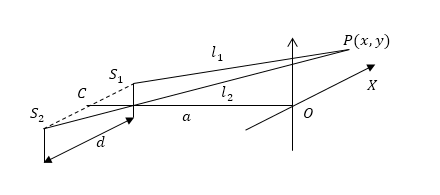
Пусть интерференционная картина наблюдается в плоскости $XOY$, перпендикулярной к нормали $CO$, проведенной к середине отрезка, соединяющего точки, в которых находятся вторичные источники света. $Ось X$ выберем параллельную отрезку $S_1S_2$ (рис.2). При этом $d$ — расстояние между отверстиями, $a$ — расстояние между отрезком $S_1S_2$ и плоскостью наблюдения.

Готовые работы на аналогичную тему

Для точки $P(x,y)$ (рис.2), которая находится в плоскости наблюдения, имеем:

Из формул (2) и (3) следует, что:

Разность путей света от источников до точки $P$ можно представить как:

Интерференционная картина будет наблюдаться только в случае, если $d\ll a$. Если $x,\ y\ll a$, то:

В таком случае имеем:

Оптическая разность хода, следовательно, равна:

При этом разность фаз имеет вид:

Так как угол $S_1PS_2$ мал, то часто считают, что волны от обоих источников движутся по одному направлению, максимумы интенсивности в таком случае будут при:

Так, интерференционная картина около точки $О$ (рис.2) состоит из интерференционных полос, которые лежат на одинаковых расстояниях и направлены под прямым углом к линии $S_1S_2$.

Необходимо отметить, что расстояние между щелями $S_<1\ >и\ S_2$ должно быть велико в сравнении с шириной щелей. Один из способов получения щелей придумал Рэлей. Он стеклянные пластинки покрывал тонким слоем серебра, делая их непрозрачными. На серебряном слое одно пластинки лезвием бритвы делалась одна линия. На другой пластинке проводили две параллельные линии. Данные линии использовались как щели.

Если применять лазеры, для опыта Юнга, то можно обойтись без первой щели.

Метод Френеля

Вторым способом создания интерференционной картины является метод деления амплитуды волны. Его смысл заключается в расщеплении волны света на полупрозрачной пластине на две когерентные волны. Фронт волны сохраняется, изменяется только направление его движения.

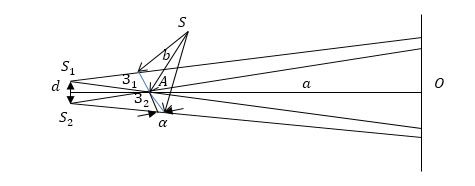
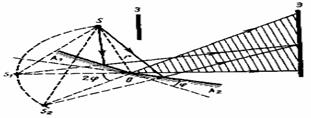
Одним из методов получения когерентных источников света в данном случае, может служить устройство, которое называют зеркалами Френеля. В этом устройстве свет от точёного источника S падает на два плоских зеркала $З_1$ и $З_2$, которые расположены под небольшим углом друг к другу ($\alpha $). При отражении свет образует два мнимых когерентных источника $S_1$ и $S_2\ (рис.3).$ Плоскость $SS_1S_2$, перпендикулярна к линии пересечения зеркал, $A$ — точка пересечения. Если расстояние $SA=b$, то $S_1A=S_2A=b$. Перпендикуляр к середине отрезка $S_1S_2$ проходит через точку $А$. Расстояние между $S_1$ и $S_2$ равно:

Угол $\varphi $, под которым из точки O видно расстояние $S_1S_2$, будет равен:

В таком случае $\triangle x$ равно:

Угол $\varphi $ можно измерить по шкале зрительной трубы. Для этого трубу размещают в точке $О$ и устанавливают ее так, чтобы отчетливо видеть изображения $S_1\ и\ S_2,\ S.\ $В таком случае легко найти длину волны $\lambda $, используя выражение:

Ширина области перекрытия световых пучков равна $2a\alpha $, значит количество интерференционных полос, которые можно наблюдать ($N$) равно:

В опыте Френеля интерференционная картина искажена дифракцией на ребре, по которому пересекаются зеркала. Полосы интерференции можно наблюдать на белом матовом экране или матовом стекле (на задней стороне).

Задание: В опыте Юнга расстояние между щелями равно $d=0,5 мм$, длина волны света $\lambda $=0,6мкм. Ширина интерференционных полос при этом равна $\triangle x=1,2\ мм.\ $Чему равно расстояние от экрана до щелей ($a$) в данном опыте?

Решение:

В опыте Юнга интерференционные максимумы наблюдаются в точках, описанных выражением:

Ширина первого интерференционного максимума при этом будет равна:

Выразим из (1.2) искомое расстояние, получим:

где для воздуха в обычных условиях $n=1$. Проведем вычисления:

Ответ: $a=1м.$

Задание: В опытах с зеркалами Френеля расстояние между мнимыми источниками света равно $d,$ расстояние от них до экрана $l$. В желтом свете ширина интерференционных полос равна $\triangle x\ .\ $Какова длина волны желтого цвета?

Решение:

Запишем условие получения интерференционных максимумов при сложении двух когерентных волн:

\[\triangle =\pm m\lambda \ \left(m=0,1,2\dots \right)\left(2.1\right),\]

где $\triangle $ — оптическая разность хода волн. Она равна (рис.4):

приравняем правые части выражений (2.1) и (2.2), получим:

\[\frac=\pm mл\to x_=\pm m\frac\lambda \left(2.3\right).\]

В таком случае запишем, что:

Ответ: $\lambda =\frac<\triangle xd>.$

Источник