Средства измерений. По способу получения числового значения измеряемой величинывсе измерения делятся на четыре основные вида: прямые, косвенные, совокупные и совместные



Классификация измерений
По способу получения числового значения измеряемой величинывсе измерения делятся на четыре основные вида: прямые, косвенные, совокупные и совместные.
Прямыми называют измерения, при которых искомое значение x измеряемой величины X находят непосредственно (прямо) из опытных данных в результате выполнения измерения. Прямые измерения – основа более сложных видов измерений.
Пример прямого измерения – измерение вольтметром напряжения источника.
Косвенныминазывают измерения, при которых искомое значение x величины X определяют на основании прямых измерений величин Y, Z, . связанных с измеряемой величиной Xизвестной зависимостью
X = F (Y, Z, . ).
Пример косвенного измерения –измерение сопротивления резистора по результатам измерения падения напряжения на резисторе и силы тока через него.
Совокупныминазывают измерения, в которых значении величин находят по данным повторных прямых измерений одноимённых величин при различных сочетаниях этих величин. Результаты совокупных измерений находят путем решения систем уравнений, составляемых по результатам нескольких прямых измерений.
Пример совокупного измерения – измерение сопротивлений резисторов, соединенных треугольником, путем измерений сопротивлений между различными вершинами треугольника и решением известной из электротехники системы трех уравнений.
Совместными называют проводимые одновременно (прямые или косвенные) измерения двух или большего числа не одноименных величин. Целью совместных измерений по существу является нахождение функциональной зависимости между величинами.
Пример совместного измерения – определение зависимости сопротивления резистора от температуры.
Rt = R0 (1 +At + Bt²)
Измеряя сопротивление резисторов при различных температурах, составляют систему уравнений, из которых находят параметры. A и B. Для повышения точности число уравнений берут больше числа неизвестных и полученную систему уравнений решают методом наименьших квадратов.
Числовое значение измеряемой величины получается путем ее сравнения с известной величиной, воспроизводимой средством измерения – мерой. В зависимости от способа применения меры известной величины выделяют две группы методов измерений (совокупности приемов использования принципов и средств измерений): непосредственной оценки и сравнения с мерой.
При методе непосредственной оценки значение измеряемой величины определяют непосредственно по отсчетному устройству измерительного прибора. Измерение силы тока с помощью амперметра – пример измерения по методу непосредственной оценки.
К методам непосредственной оценки относятся прямые измерения, за исключением методов, основанных на непосредственном сравнении размера измеряемой величины с размером величины, воспроизводимой мерой.
Методы сравнения с мерой – методы, при которых производится сравнение измеряемой величины и величины воспроизводимой мерой. Отличительной особенностью методов сравнения является непосредственное участие в процессе измерения меры известной величины, однородной с измеряемой.
Группа методов сравнения с мерой включает в себя следующие методы: компенсационный, противопоставления, нулевой, дифференциальный, замещения и сопоставления.
Компенсационный метод измеренийсостоит в том, что на вход сравнивающего устройства одновременно воздействуют, измеряемая величина и одноименная ей величина, размер которой воспроизводится мерой, а соотношение между их размерами определяется по выходному сигналу сравнивающего устройства. Пример: измерение напряжения постоянного тока с помощью компенсатора путем сравнения с э.д.с. нормального элемента.
Метод противопоставления – метод измерений, при котором измеряемая величина и величина, размер которой воспроизводится мерой, одновременно воздействуют на разные входы прибора сравнения, по выходному сигналу которого определяется соотношение между размерами этих величин. Пример: взвешивание на равноплечих весах.
При нулевом методе измерения разность измеряемой величины и известной величины или разность эффектов, производимых измеряемой и известной величинами, сводится в процессе измерения к нулю, что фиксируется высокочувствительным прибором – нуль – индикатором. Пример: измерение сопротивления резистора с помощью четырех – плечного моста, в котором падение напряжения на резисторе с неизвестным сопротивлением уравновешивается падением напряжения на резисторе известного сопротивления.

Дифференциальный метод состоит в том, что разность измеряемой величины и величины известной, воспроизводимой мерой, измеряется с помощью измерительного прибора. Неизвестная величина определяется по известной величине и измеренной разности. В этом случае уравновешивание измеряемой величины известной величиной производится не полностью и в этом заключается отличие дифференциального метода от нулевого.
При методе замещения производится поочередное подключение на вход прибора измеряемой величины и известной величины и по двум показаниям прибора оценивается значение неизвестной величины. Примером этого метода является точное измерение малого напряжения с помощью высокочувствительного гальванометра, к которому сначала подключают источник неизвестного напряжения и определяют отклонение указателя, а затем с помощью регулируемого источника известного напряжения добиваются того же отклонения указателя. При этом известное напряжение равно неизвестному.
При методе совпадения измеряют разность между измеряемой величиной и величиной, воспроизводимой мерой, используя совпадение отметок шкал или периодических сигналов. Примером этого метода является измерение частоты вращения объекта с помощью стробоскопа.
Источник
Виды измерений
Числовое значение величины находят путем измерения, т. е. узнают, во сколько раз значение данной величины больше или меньше значений величины, принятого равным единицы. По способу получения числового значения измеряемой величины все измерения делят на прямые, косвенные, совокупные и совместные.
Прямым называют измерение, при котором искомое значение величины находят непосредственно из опытных данных.
Уравнение прямого измерения имеет вид
где А – значение измеряемой величины в принятых для нее единицах измерения; с – цена деления шкалы или единичного показания цифрового отсчетного устройства в единицах измеряемой величины; х – отсчет по индикаторному устройству в делениях шкалы.
Например, измерение диаметра вала штангенциркулем будет прямым, так как оно дает непосредственно значение диаметра вала.
Если же вал имеет диаметр, равный нескольким метрам, то измерить его штангенциркулем очень сложно. В этом случае измеряют длину окружности, т.е. диаметр вала измеряют косвенно.
Косвенным называют измерение, результат которого определяют на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью.
Уравнение косвенного измерения имеет вид
Где А – искомая величина, являющаяся функцией аргументов , измеренных прямым методом.
Например, удельное электрическое сопротивление проводника можно найти по его сопротивлению, длине и площади поперечного сечения.
Косвенные измерения широко применяют в измерительной технике: при измерении сферической поверхности оптической линзы, когда реально существует лишь часть этой поверхности, или в тех случаях, когда выполнять прямые измерения невозможно, например при измерении плотности твердого тела, определяемой обычно по результатам измерений объема и массы.
Совокупными называют проводимые одновременно измерения нескольких величин, при которых значения искомых величин находят решением системы уравнений, получаемых при прямых измерениях. Например, измерения, при которых массы отдельных гирь набора находят по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь.
Совместными называют производимые одновременно измерения двух или нескольких неодноименных величин для нахождения функциональной зависимости между ними. Например, измерения, при которых электрическое сопротивление при температуре 20 °C и температурные коэффициенты измерительного резистора находят по данным прямых измерений его сопротивления при различных температурах.
Большинство измерений в настоящее время выполняют на производстве и используют при осуществлении контроля за качеством выпускаемой продукции и параметрами технологического процесса. Под контролем понимают измерение, в процессе которого определяют, находится ли значение измеряемой величины в заранее установленных для нее пределах. Контроль в зависимости от его непосредственного влияния на технологический процесс подразделяют на активный и пассивный.
Активный контроль оказывает воздействие на технологический процесс непосредственно в ходе изготовления контролируемых изделий. От его точности зависит качество выпускаемой продукции. Например, при шлифовании на автоматическом станке, когда прибор «следит» за размером диаметра шлифуемой детали, он связан с рабочими органами станка и с помощью промежуточных устройств управляет этими органами. Одним из видов активного контроля является подналадка, заключающаяся в том, что по показаниям контролирующего прибора устраняют рост систематической погрешности.
Пассивный контроль позволяет только констатировать факт, находятся или не находятся в заданных пределах физические параметры контролируемого объекта. Пассивный контроль осуществляют при разбраковке изделий на годные и негодные. Когда разбраковывают изделия, то часто не только отделяют годную партию от брака, но и брак сортируют на исправимый и неисправимый. Контроль осуществляют одним из двух способов: проверкой каждого из элементов или параметров, от которых зависит это свойство (поэлементный контроль), или одновременной проверкой комплекса элементов, при которой непосредственно контролируется требуемое свойство изделия (комплексный контроль).
Поэлементный контроль имеет ряд преимуществ: не требует создания специальных средств измерений; позволяет осуществлять выборочный контроль; дает возможность оценить точность каждого из элементов изделия, а следовательно, наметить пути дальнейшего совершенствования технологического процесса. Однако при использовании поэлементного контроля возможны ошибки. Например, изделие может быть забраковано по одному из элементов, хотя его отклонение компенсируется точным изготовлением других элементов и изделие обладает требуемым свойством, т. е. годно, или если разработчику не удалось выявить все элементы, от которых зависит данное свойство изделия, и часть из них не контролируется, то может быть пропущен брак.
Ценность комплексного контроля заключается в том, что его использование позволяет избежать ошибок первого и второго рода, возникающих при поэлементном контроле, так как он дает возможность непосредственно установить годность или негодность изделия.
Источник
Способ получения числового значения измеряемой величины
1. Методы измерений.
2. Погрешности измерений.
3. Выбор метода и средств измерений.
4. Выбор измерений.
1. Методы измерений . Измерение физической величины может быть осуществлено различными методами (способами), выбор которых в каждом отдельном случае зависит от характера измеряемой величины, от условий измерения, от устройства и принципа действий измеряемой аппаратуры, а также требуемой точности.
По способу получения числового значения измеряемой величины методы измерения делят на 3 вида:
Они различаются по характеру использования мер.
К наиболее важным методам, прямых измерений постоянно встречающихся на практике, относятся следующие:
1. Метод непосредственной оценки.
2. Метод сравнения, состоящий из четырех разновидностей:
а) нулевой метод;
б) дифференциальный метод;
в) метод замещения;
г) метод совпадения.
Сущность метода непосредственной оценки Состоит в том, о значение измеряемой величины судят по показанию одного или нескольких приборов прямого преобразования, заранее проградуированных в единицах измеряемой величины или в единицах других величин, от которых зависит измеряемое. Он принадлежит к числу наиболее распространенных в технической практике (в силу своей простоты), и типичным его примером служит измерение электрических величин стрелочными приборами. Точность этого метода обычно ограничивается точностью измерительных приборов. Отличительной особенностью этого метода является то, что мера непосредственного участия в процессе измерения не принимает.
Сущностью метода сравнения является то, что при использовании этих методов измеряемая величина в процессе измерения сравнивается с величиной, воспроизводимой мерой.
Таким образом, отличительной чертой методов сравнения является непосредственное участие меры в процессе измерения. Они различаются по характеру использования мер.
А) Нулевой метод – это метод, при котором результатирующий эффект воздействия измеряемой величины и образцовой меры на прибор сравнения (нулевой индикатор) доводится до нуля. Примерами использования нулевых методов в электротехнике являются мостовые и компенсационные схемы. Нулевые методы значительно сложнее методов непосредственной оценки, требуют значительно большего времени, но зато точность их несравненно выше (0,02% и выше).
Нулевые методы применяются в основном при проверке приборов используемых непосредственной оценке.
Б) Дифференциальный метод – это метод, при котором непосредственно оценивается измерительными приборами разность между измеряемой величиной и образцово мерой или разность производимых ими эффектов.
Аиз-А=а
Аиз – измеряемая величина; А – показание прибора; а – погрешность.
Зная А и измерив а, можно найти Аиз. Точность этого метода тем выше, чем меньше измеряемая разность и с тем большей точностью она измерена (если разность между Аиз и А составляет 1% и измерено с точностью до 1%, то точность измерения составит уже 0,01%).
Дифференциальные методы используются при точных лабораторных измерениях (поверка образцовых сопротивлений, поверка измерительных трансформаторов и др.).
В) Метод замещения . Этот метод заключается в том, что в процессе измерения измеряемая величина Аиз заменяется в измерительной установки известной величиной А, при чем путем измерения величины А, измерительная установка приводится в прежнее состояние, то есть достигаются те же показания приборов, что и при действии величины Аиз. При таких условиях Аиз=.
Г) Метод совпадения . Этот метод заключается в том, что измеряют разность между искомой величиной и образцовой мерой, используя совпадения меток шкал или периодических сигналов. Сущность этого метода можно пояснить на примере определения размера дюйма.
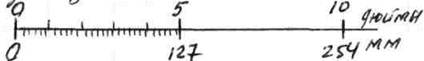 |
Погрешности измерений.
При осуществлении измерений, вследствие ряда причин, числовое значение измеряемой величины, полученная в результате опыта, является лишь более менее приближенным.
Отклонение результатов измерения от истинного значения измеряемой величины называется Погрешностью измерения .
Верным (истинным) значением Изменяемой величины называют ее значение, свободное от погрешностей измерений.
Действительное значение – это значение, полученное в результате измерения с допустимой погрешностью (ошибкой).
Погрешности измерений можно классифицировать по ряду признаков:
1. По способу числового выражения погрешности измерений делятся на:
А) Абсолютные и б) относительные.
Абсолютной погрешностью Называется разность между измеренным и действительным значением измеряемой величины.
За действительные значения измеряемой величины принимаются показания образцового прибора.
Абсолютная погрешность измеряется в единицах измеряемой величины.
Величина обратная по знаку абсолютной погрешности называется поправкой.
σ =-ΔА
Относительной погрешностью Называется отношение абсолютной погрешности к действительному значению измеряемой величины.
β = ΔА/АД = Аиз – Ад/Ад; или β = ΔА/Ад·100%.
2. По характеру изменения Погрешности измерений делятся на:
В) грубые ошибки (промахи).
Систематическими Называются погрешности, подчиняющие определенному закону или остающиеся в
Процессе измерения постоянными. К ним относятся погрешности, обусловленные неточностью осуществления меры, неправильностью градуировок измерительного прибора, влиянием температуры окружающей среды на меры и измерительные приборы.
Различают следующие разновидности систематических погрешностей:
2. Погрешности установки прибора.
3. Личные погрешности (субъективные).
4. Погрешности метода (или теоретические).
В зависимости от изменения во времени систематические погрешности делятся на: а) постоянные; б) прогрессивные; в) периодические.
Для учета и исключения систематических погрешностей необходимо располагать, возможно, полными данными о наличии отдельных видов погрешностей и о причинах их возникновения.
Систематические погрешности могут быть исключены или значительно уменьшены устранением источников погрешностей или введением поправок, останавливаемых на основании предварительного изучения погрешностей, путем поверки мер и приборов, используемых при измерении, введением поправочных формул и кривых, выражающих зависимость показаний приборов от внешних условий.
Случайными Называются погрешности, изменение которых не подчиняется какой-либо закономерности. Они обнаруживаются при многократном измерении искомой величины, когда повторные измерения проводятся одинаково тщательно и, казалось бы, при одних и тех же условиях.
Случайные погрешности нельзя исключить опытным путем, но их влияние на результат измерения может быть теоретически учтено путем применения при обработке результатов измерений методов теории вероятности и математической статистики.
Грубые ошибки – это погрешности, существенно превышающие ожидаемые при данных условиях. Примером грубых ошибок могут быть неправильные отсчеты показаний средств измерений. Грубые погрешности измерения выявляются при повторных измерения и должны быть отброшены, как на заслуживающие доверия.
Общие методы повышентя точностсти средств измерений.
Стремясь к созданию более точных средств измерений измерительная тезника выработала ряд общих методов достижения точности, которые можно подразделить на четыре группы:
1. Стабилизация важнейших параметров средств измерений технологическим путем, т. е. путем использования наиболее стабильных деталей, материалов и соответствующей технологии изготовления.
2. Метод пассивной защиты от быстро изменяющихся влияющих величин, т. е. уменьшение случайных погрешностей средств измерений путем применения фильтрации, амортизации, теплоизоляции и т. д.
3. Методы активной защиты от медленно изменяющихся влиящих величин путем стабилизации этих величин.
4. Методы коррекции систематических и прогрессирующих погрешностей и статическая обработка случайных погрешностей.
Повышение точности измерений обычно связано с усложнением аппаратуры и увеличением времени
(большая повторность) измерения. А это не всегда оравдано. Очевидно также нецелесообразность особой точности измерения величин, мало влияющих на числовое значение общего конечного результата.
Так, например, при измерении величин x1, x2 и х3 для определения величины у=х12*х2β*х3γ вряд ли целесообразно добиваться особой точности измерения х1, если показателем степени α =1, β = 2, γ = 3.
Требуемеая точность должна соответствовать задачам и условиям измерений.
Выбор метода и средств измерений.
При выборе метода измерений следует руководствоваться требуемой точностью результатов измерений.
По точности получаемых результатов можно разделить на три группы:
1. Результат измерения должен иметь максимальную возможную при существующем уровне измерительной техники точность.
Такие измерения называют Точными (презиционными). Например, измерения физических констант, эталонный измерения, некоторые спеиальные измерения, относящиеся к максимально точной работе отдельных приборов.
2. Измерения, погрешности результата которых не должена превосходить некоторого заданного значения.
Такие измерения называют Контрольно поверхностными. Они выполняются в поверочных контрольно-измерительных лабораториях такими измерительными средствами и по такой методике, чтобы гарантировать погрешность результата, не превышающую некоторого заранее заданного значения.
3. Измерения, при которых погрешность результата определена характеристиками измерительных устройств.
Такие измерения называют Техническими.
К ним относятся и лабораторные измерения, проводимые при различного рода обработок и исследованиях, и исследованиях, и производственные, и приемно-сдаточные, и эксплутационные измерения, проводимые для обеспечения необходимого режима работы различных объектов и устройств.
Приборы для измерений выбирают по ряду показателей: роду тока, частоты, диапозону измеряемой величины, точности, входным параметрам, степени влияния внешних факторов.
1. Род тока исследуемой цепи определяет принцип действия и систему выбираемого для нее измерительного прибора. (U, I, R на постоянном токе – МЭ, Р-ЭД, точное измерение I, U, P, cosγ вольтметру – ср. Д., измерения средних, действующих значений тока и напряжения в цепях передоваемого тока звуковой и высокой частоты применяют – выпрямительные, тэрмоэлектрические, электронные и электростатические приборы. Мгновнные значения переменных величин измеряют – осцелографами).
2. Номинальная чатота или область частоты измерительного прибора или меры должна соответствовать частоте тока исследуемой цепи.
Чем сильнее отличается частота исследуемой цепи от номинальной частоты прибора или меры, тем больше погрешности измерений.
3. Номинальные пределы прибора или меры не должны превышать верхнего предела измеряемой величины более чем на 25%.
Чем сильнее они разняться, тем менее точны результаты измерений. При заданном классе точности допускается относительная погрешность прибора или меры тем больше, чем меньше измеряемая величина.
4. Классы точности выбранного измерительного прибора или меры должны быть такими, чтобы допустимые основные погрешности были в 3 раза меньшими, чем допустимые погрешности данных измерений, т. к. предельная погрешность измерений, возможная в данных условиях, не может превысить
Утроенного значения среднеквадратичной погрешности ряда измерений.
5. В зависимости от схемы включения измерительного прибора его входное сопротивление должно быть, возможно, большим или меньшим.
Чем точнее измерения, тем большими должны быть входные сопротивления измерительных приборов включаемых параллельно, и тем меньшими они должны быть у приборов, включаемых последовательно в исследуемую цепь.
6. Выбирая нужный измерительный прибор, следует учитывать конкретные условия измерений и технические характеристики прибора.
Непосредственное влияние внешних факторов может вызвать большие погрешности приборов (температура, влажность, внешние электрические и магнитные поля, паразитные емкости). При любых условиях наиболее желательны приборы и меры, требующие минимальных средств защиты от влияния внешних факторов.
Виды измерений.
Прцесс измерения может осуществляться по-разному в зависимости от рода измеряемой величины и приемов измерения.
По способу получения результатов различабт следующие виды измеренй:
2. Косвенные измерения.
3. Совокупные измерения.
К прямым измерениям Относятся измерения, результат которых получается непосредственно из опытных данных измерения.
Прямое измерение условно можно выразить формулой Y=Х, где
Y – искомое значение измеряемой величины;
Х – значение, непосредственно получаемоеиз опытных данных.
К этому виду измерений относятся измерения различных физичских величин при помощи приборов, градуированных в установленных единицах (ток – апмерметром, температура – термометром). К этому виду измерений относятся и измерения, при которых искомое значение величины определяется непосредственным сравнением ее с мерой.
Косвенными Называется такое измерение, при котором искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвеных измерениях числовое значение измеряемой величины определяют путем вычисления по формуле.
Y = F (X1, X2, … , Xn),
где y – искомое значение измеряемой величины;
x1, x2, …, xn – значения измеренных величин (R = U/I, P = U*I – в цепях постоянного тока).
Совокупными Называются такие измерения, при коорых искомые значения величин определяются путем решения системы уравнений, связывающих значения искомых величин с непосредственно измеренными величинами, т. е. путем решения системы уравнений.
Примером этого вида измерений является определение температурных коэффициентов сопротивления:
Rt = R20 [1+α (T1-20)+β(T1-20)]
Здесь Rt и t измеряются прямым измерением, а α, β и R20 – искомые величины.
Меняя тепловой режим катушки и измеряя Rt при ряде заданных температур t1; t2 и t3, получаем систему уравнений, совместное решение которых позволяет определить числовые значения искомых величин.
Источник







