Уравнивание превышений нивелирной сети способом полигонов
5.6 Уравнивание превышений нивелирной сети способом полигонов
Этот способ предложен профессором Поповым В. В. Способ основан на строгом уравнивании по способу наименьших квадратов. Он позволяет составлять нормальные уравнения коррелат непосредственно по схеме сети. Решение нормальных уравнений производится последовательными приближениями. Практически это сводится к последовательному распределению невязок в каждом замкнутом ходе пропорционально длинам ходов или числу станций в ходе (пропорционально обратным весам отдельных ходов). Не рассматривая составление нормальных уравнений коррелат и их решение, приведем практическое применение этого способа.
На схеме сети (рис. 5.7) показывается:
— длины отдельных ходов (звеньев),км (на рис. 57 они записаны в кружках;
— номера ходов — N1 — N8;
— номера полигонов I , II , III , IV и их невязки .
В каждом полигоне сплошными линиями вычерчиваются рамки, в которые записываются невязки полигонов. Возле каждого звена вычерчивается рамка поправок (пунктирной линией) вне каждого полигона.
Длину каждого хода (для удобства вычислений) целесообразно выразить в частях, по отношению к периметру отдельного полигона принятого за 1 или 100. Эти числа записываются другим цветом (красные числа) над рамками (штриховыми) поправок за каждым замкнутым полигоном.
В первом полигоне периметр равен
км
На основании этого вычисляются «красные» числа:
— для звена ВС ,
Рисунок 5.7- Схема уравнивания превышений нивелирной сети способом полигонов
— для звена ВЕ .
Контролем является равенство суммы «красных» чисел единице:
Во втором полигоне периметр и «красные» числа равны
км
— для звена С D ,
— для звена D Е ,
— для звена СЕ .
Контроль: 
В третьем полигоне находим:
км
— для звена D А ,
— для звена D Е
— для звена АЕ
Контроль: 
В четвертом полигоне находим:
км
— для звена АВ
— для звена ВЕ ,
— для звена АЕ .
Контроль: 
После этого производится распределение невязок, начиная с полигона I (можно с любого) на звенья, образующие этот полигон.
В полигоне I умножением невязки этого полигона, равной + 15 мм на «красные» числа соответствующих звеньев, получают поправки в превышения звеньев, образующих этот полигон. Полученные величины записываются в рамки поправок у соответствующих звеньев с тем же знаком:
в звено ВС — + 15 мм · 0.42 = + 6 мм,
в звено СЕ — + 15 мм · 0.33 = + 5 мм,
в звено ВЕ — + 15 мм · 0.25 = + 4 мм.
Величины поправок округляются до 1 мм, так чтобы сумма поправок в звенья равнялась невязке соответствующего полигона.
В полигоне II невязка была равной (- 12) мм, но в звено СЕ из первого полигона прибавлена поправка (+ 5) мм. В связи с этим невязка в этом полигоне оказалась равной (- 12) мм (+ 5) мм = (- 7) мм. Эту невязку записывают в рамку невязок полигона II и умножая ее на «красные» числа звеньев получают поправки:
в звено СD: (- 7 мм · 0.43) = -3 мм,
в звено D Е: (- 7 мм · 0.26) = — 2 мм,
в звено СЕ: (- 7 мм · 0.31) = -2 мм.
В полигоне III невязка была равна (- 
мм и из полигона II получена поправка в звено D Е равная (- 2) мм. Поэтому невязка стала равной (- мм + (- 2) мм = — 10 мм, которая помещается в рамку невязок и распределяется как в предыдущих полигонах умножением на «красные» числа звеньев полигона III :
В звено А D: ( — 10 мм · 0.46 )= — 5 мм,
в звено АЕ: (- 10 мм · 0.28) = — 3 мм,
в звено D Е: ( — 10 мм · 0.26) = — 2 мм.
В полигоне IV невязка равна (- 11) мм и получены поправки в звено ВЕ из полигона I (+ 4) мм, и в звено AE из полигона III (- 3 мм), поэтому невязка оказалась равной (- 11 мм) + 4 мм + (- 3 мм) = — 10 мм. Она записывается в рамку невязок этого полигона и распределяется умножением ее на «красные» числа звеньев полигона IV :
в звено АВ: ( — 10 мм · 0.46) = — 5 мм,
в звено ВЕ: (- 10 мм · 0.24) = — 2 мм,
в звено АЕ: ( — 10 мм · 0.30) = — 3 мм.
Эти вычисления составляют первый круг уравнивания (первое приближение). Во втором круге вычисления повторяются, но с новыми невязками полигонов с учетом поправок из первого круга вычислений.
В полигоне I поправки из первого круга в звенья СЕ равная (- 2) мм и в ВЕ — (- 2 мм) образуют новую невязку полигона f 1 =( — 2 мм )+ (- 2 мм) =( — 4) мм , которая записывается в рамку поправок и распределяется как в первом круге умножением на «красные» числа звеньев полигона I :
в звено ВС: –( — 4 мм · 0.42) = (- 2) мм,
в звено СЕ: ( — 4 мм · 0.33) = (- 1) мм,
в звено ВЕ : ( — 4 мм · 0.25) = (- 1) мм.
В полигоне II поправка в звено D Е из первого приближения равна (- 2) мм и в СЕ из второго приближения (- 1) мм образуют новую невязку полигона f II = — 2 мм + (‑1мм) = -3 мм, которая записывается в рамку невязок и распределяется как в первом круге умножением на «красные» числа звеньев полигона II:
в звено С D: (- 3 мм · 0.43) = (- 1) мм,
в звено D Е: ( — 3 мм · 0.26) = (- 1) мм,
в звено СЕ: (- 3 мм · 0.31) = (- 1) мм.
В полигоне III поправка в звено АЕ из первого приближения вычислений равна (- 3) мм, а в звено D Е из второго круга (- 1) мм, образуют невязку 
= — 3 мм + (- 1 мм) = — 4 мм, которая записывается в рамку невязок и распределяется как в первом приближении; полученные поправки записываются в соответствующие рамки поправок:
в звено А D: ( — 4 мм · 0.46) = (- 2) мм,
в звено АЕ: (- 4 мм · 0.28) = (- 1) мм,
в звено D Е: ( — 4 мм · 0.26) = (- 1) мм.
В полигоне IV поправка из второго приближения в звено АЕ равна (- 1) мм и в звено ВЕ (- 1) мм образуют невязку 
= — 1 мм + (- 1 мм) = — 2 мм, которая записывается в рамку невязок и распределяется по звеньям этого полигона:
в звено АВ: ( — 2 мм · 0.46) =( — 1) мм,
в звено АЕ: ( — 2 мм · 0.30) = (- 1) мм,
в звено ВЕ: ( — 2 мм · 0.24) = 0 мм.
В третьем круге (приближении) вычисления ведутся аналогично второму кругу, но невязки полигонов определяются по поправкам полученным из второго и третьего круга:
В полигоне I: 
= (-1) + (0) = — 1 мм, а поправки в звенья этого полигона равны: — 1,0; 0 мм. В полигоне II: 
= 0 + (-1) = 1 мм, а поправки в звенья этого полигона равны: — 1,0 ; 0 мм.
В полигоне III: = 0 + (-1) = — 1 мм, а поправки в звенья полигона равны: — 1,0 ; 0 мм.
В полигоне IV: 
= 0 +0 = 0, т.к. поправки из третьего приближения в звенья АЕ и ВЕ равны нулю.
Как видно из этих вычислений для уравнивания достаточно трех приближений. После этого необходимо подсчитать поправки в каждое звено. Для этого в рамках поправок суммируются поправки, полученные из каждого приближения.
Для периферийных звеньев после сложения поправок в рамке надо поменять знак на обратный и записать поправку у соответствующего звена (на рис. 5.7 поправки записаны в скобках). Поправки в превышения периферийных звеньев равны: АВ — (+ 6 мм) , ВС — (- 3 мм), С D — (+ 5 мм), А D — (+8мм).
Для общих звеньев СЕ , D Е , АЕ , ВЕ поправки находятся как разности поправок в эти звенья из смежных полигонов :
в звено СЕ полигона I: (-3) — (+4) = — 7 мм
в звено СЕ полигона II: (+4) — (-3) = + 7 мм
в звено D Е полигона II: (-3) — (-3) = 0 мм
в звено D Е полигона III: (-3) — (-3) = 0 мм
в звено АЕ полигона III: (-4) — (-4) = 0 мм
в звено АЕ полигона IV: (-4) — (-4) = 0 мм
в звено ВЕ полигона IV: (+3) — (-2) = + 5 мм
в звено ВЕ полигона I: (-2) — (+3) = — 5 мм.
Для контроля необходимо в каждом полигоне подсчитать сумму поправок в звенья и сравнить ее с первоначальной невязкой полигона. Эти две величины должны быть одинаковы по абсолютному значению, но противоположны по знаку.
Полигон I: (-3) + (-7) + (-5) = — 15 мм, невязка + 15 мм.
Полигон II: (+5) + (0) + (+7) = + 12 мм, невязка — 12 мм.
Полигон III: (+8) + (0) + (0) = + 8 мм, невязка — 8 мм.
Полигон IV: (+6) + (+5) + (0) = + 11 мм, невязка — 11 мм.
При уравнивании нивелирной сети по способу полигонов В.В. Попова все вычисления производятся непосредственно на схеме (чертеже) сети.
Недостатком этого способа уравнивания является сложность оценки точности по результатам уравнивания.
Источник
Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4. Уравнивание ходов технического нивелирования способом полигонов профессора В.В. Попова
4.1 Общие указания и исходные данные
Простой и в то же время строгий способ уравнивания ходов технического нивелирования способом полигонов предложил профессор В.В.Попов. Этот способ сводится к последовательному распределению невязок в каждом полигоне пропорционально длинам ходов. При этом если в соседнем полигоне уже было произведено распределение невязок, то на величину поправки, пришедшейся на общий обоим полигонам ход, нужно предварительно исправить с учётом её знака невязку этого подлежащего увязанию полигона. Таким образом, дело сводится к методу последовательных приближений. Применение способа Попова требует расположения вычислений в определенной схеме. Удобно эти вычисления производить на схеме расположения ходов, как это рекомендует сам автор.
Перед уравниваем я вычертила схему нивелирной сети (приложение Г), на которую выписала по ходам и полигонам периметры, измеренные превышения, фактические и допустимые невязки в сумме превышений по полигонам. Для установления знака невязки направление обхода в каждом полигоне выбрала по ходу часовой стрелки. Контролем правильности вычисления невязок является условие [fh]=0. вычислила допустимые невязки по формуле:
где L – периметр полигона, км.
Предварительно исправила исходные данные, учитывая свой порядковый номер. Эти вычисления производятся в таблице 11. Длину ходов вычислила по формуле: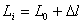 
, (24),
∆l = +0.2км * №=0,16 км. Высота исходных реперов HRp1=106.985 –
4.2 Уравнивание превышений по способу полигонов профессора В.В.Попова
Далее вычертила схему независимых нивелирных полигонов, на которую выписала невязки полигонов (приложение Д). Невязки в превышениях выписаны внутри соответствующих полигонов в прямоугольных рамках. Полигоны пронумерованы.
Рядом с ходами, идущими по периметру полигонов, подготовила таблички для записи значений поправок. Поправки по каждому ходу выбрасывались за полигон, таким образом для внутренних ходов – по две таблички и по одной с каждой внешней стороны.
Для каждого хода вычислила коэффициент пропорциональности или «красные числа» по формуле:
ri=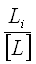 
(25),
где Li – длина хода, [L] – периметр хода. Найденные отношения выписала на схему над табличками поправок для каждого хода красным цветом. Контролем правильности вычисления этих чисел является равенство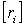 
= 
по каждому полигону (например, для полигона I «красные числа» получились 0.22, 0.25, 0.28, 0.25, в сумме они действительно дают единицу).
Начала распределение невязок с полигона, имеющего наибольшую по абсолютной величине невязку. В моем варианте этим полигоном является полигон II с невязкой -14. Невязки в полигонах распределяют пропорционально «красным числам». Итак, умножала невязку полигона на соответствующие этому полигону «красные числа», округляя до целых, и записывала в таблички, лежащие вне полигона, причем со знаком, одинаковым знаку невязки. Контролем является: сумма поправок должна дать величину невязки.
Перешла к следующему полигону (III). В нем ход 12-13 уже получил поправку, поэтому невязку этого полигона следовало изменить на величину поправки хода 12-13. Полученная остаточная невязка вписывается в рамку под числом исходной невязки полигона III. Далее эту остаточную невязку умножала на соответствующие этому полигону «красные числа». Полученные поправки выписываем в рамки, находящиеся вне этого полигона. Каждый раз производила контроль вычислений!
И так далее, переходила к следующему полигону по часовой стрелке и выполняем те же операции (исправляла исходную невязку полигона с учетом поправок, пришедших из других полигонов, и распределяла поправки пропорционально «красным числам», выполняя контроль). Так, когда вернулась к полигону II, значит завершила первый круг распределения невязок. Перешла ко второму кругу, повторяя все в том же порядке.
В полигоне II невязку я уже распределила, но в этом полигоне имеются поправки, пришедшие из других полигонов. Сложив их, получила новую невязку этого полигона, которую должна распределить вышеописанным порядком, вписывая вторичные поправки по ходам в соответствующие рамки.
Таким же путем прошла по всем другим полигонам во втором круге. После перешла к третьему, четвертому и так далее. В моем случае, потребовалось пройти 5 кругов.
Теперь необходимо в каждой рамке подсчитать алгебраическую сумму поправок. Для внешних ходов нужно у найденных результатов сложения по каждому ходу изменить знак на обратный и перенести внутрь полигона. Так, например, у хода 2-12 поправка равна -19, перенеся ее внутрь II-ого полигона, получим поправку для хода 2-12, равную 19. Для общих ходов каждой пары смежных полигонов имеются по две рамки, расположенные по разные стороны хода. Вычислила поправки по каждому ходу как разность между суммами поправок по внутренней и внешней табличкам. Эти величины вписала при данном ходе, каждую внутри соответствующего полигона.
Контролем служит то, что сумма поправок по всем ходам полигона должна дать взятую с обратным знаком величину первоначальной невязки, приходящуюся на данный ход (в моем случае по каждому полигону получилось, что сумма поправок по всем ходам совпала с первоначальной невязкой, взятой с противоположным знаком:
по I полигону – 12 мм, по II – 14 мм , по III — 8 мм, по IV — 14 мм, по V – 12мм).
Источник
