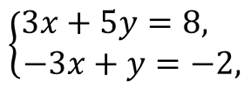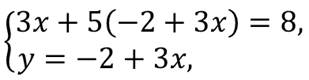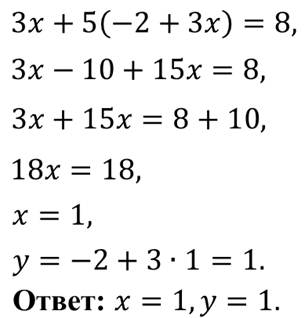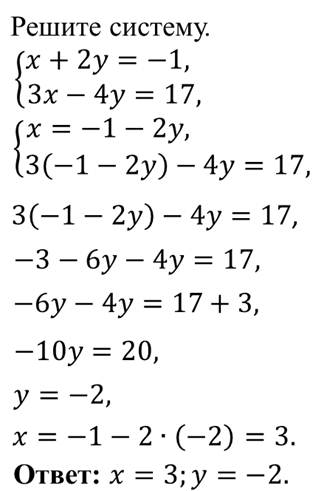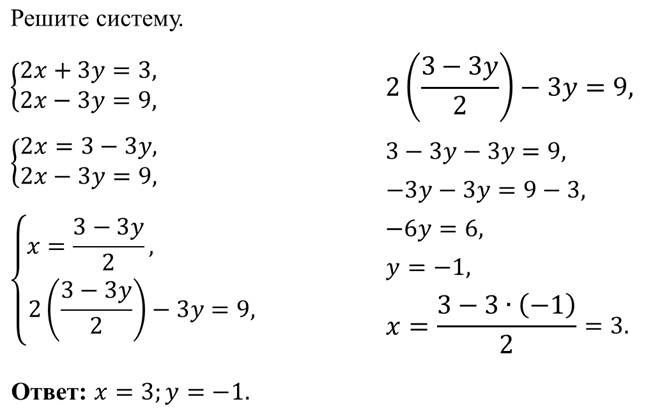Способ подставки математика 7 класс

Конспект урока по математике на тему «Метод подстановки», 7 класс

Открытый урок: «Метод подстановки» 7 класс

Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способами подстановки.

Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.

Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.

Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.

Методы: частично – поисковый, коллективный, групповой, индивидуальный.

Тип урока: урок открытия новых знаний

Оборудование: мультимедийное оборудование, проектор, экран, жетоны, раздаточный материал.

Литература: Учебник А.Г. Мордковича Алгебра 7. Издательство «Мнемозина» 2007.

№1. Организационный момент:

Приготовились к уроку, встали у своих мест.

-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.

Улыбнитесь себе, друг другу и мне, мы дружно и с хорошим настроением начинаем работать.

Унынье и лень уничтожить на нуль.

№2. Проверка домашнего задания

—Пока мы будем проверять домашнее задание, у доски нам решит систему графическим методом…(вызвать ученика к доске, задание на карточке).

. Открыли тетради, взяли красную пасту, проверяем:

-У кого не было ошибок, может поставить себе «5», у кого были помарки, исправления, неточности – красной пастой пишут: Домашнее задание проверено.

№3. Актуализация опорных знаний

На прошлом уроке мы с вами познакомились с новой математической моделью.

Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.

-Кто может мне сказать:

Что называется решением системы двух линейных уравнений с двумя переменными

-А что значит решить систему двух линейных уравнений с двумя переменными?

-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).

-Дома, я также просила поработать вас с текстом параграфа №11, и найти ответ на вопрос: Почему для нас графический способ решения системы двух линейных уравнений имеет большое значение?». Кто нашел ответ на этот вопрос?

—ученик закончил решение системы. Сейчас он прокомментирует нам ее решение.

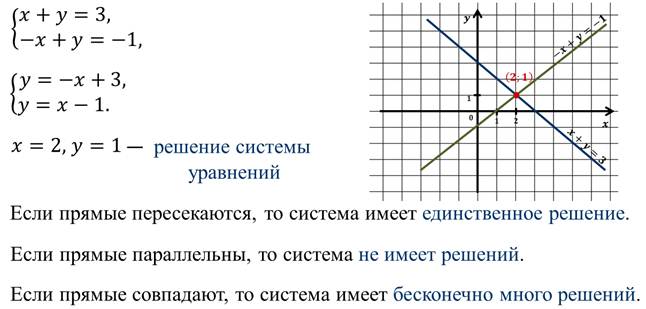
-А сейчас, внимание на экран, я хочу показать вам решение графическим методом еще одной системы:

— На чертеже: построен синим цветом график первого линейного уравнения и зеленым цветом график второго уравнения. Как видите, графики пересекаются.

Координаты точки пересечения графиков и будут являться решением данной системы. Координаты данной точки являются решением и первого и второго линейных уравнений, т.к. точка принадлежит и первому и второму графикам функций. Однако, чему конкретно равны абсцисса и ордината точки, определить очень сложно. Точка «висит» внутри определенной клеточки.

Из этого примера видно, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с дробными значениями координат точки.

Этим мы и займемся сегодня на уроке.

—В тетрадях запишите, пожалуйста, число, Классная работа.

Тема урока: «Метод подстановки». Как вы думаете, какова цель нашего урока? Молодцы, правильно.

Джордж Бернард Шоу сказал: «Деятельность – единственный путь к знаниям».

— Как вы думаете, какой смысл заложен в этом изречении? (высказывания ребят).

-Правильно, ребята. Поэтому я предлагаю вам провести наш урок под этим девизом. За активную работу предусмотрены жетоны.

Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. И так:

№1. Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)

(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)

Ответ: у=2,5х у=8-1,5х.

№2. Попробуем решить систему, которою решал на доске ….(ученик, вызванный ранее) другим способом: (учитель начинает рассуждение, затем продолжают ученики)

Преобразуем эту систему к виду:

Вспомним, какие задания с такой формой записи мы решали с вами ранее? (Вопрос классу)

-Ответ: Найти точку пересечения графиков двух данных функций

Кто может пойти к доске и выполнить это задание? (К доске…)

-Нас интересует такое значение х, при которых:

Ответ(2;5)

-Чем эти рассуждения отличались от тех, которые применял ….(имя ученика) при решении этой системы графическим методом?

-Откройте, пожалуйста, учебник на странице 65 и, прочитав текст, ответьте мне на этот вопрос.

-Как же мы рассуждали? Еще раз по учебнику прочитает нам………..

-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?

В учебнике найдите алгоритм решения и внимательно прочитайте его.

-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.

Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.

-Давайте вернемся к системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)

Ответ: ( 2,4 ;2,2)

Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)

Этап№ 5. Физкультминутка

Комплекс упражнений + зарядка для глаз.

Этап № 6. Фронтальный устный опрос

1) Что называют решением системы уравнений с двумя переменными? Что значит решить систему уравнений?

2) Способы решения систем линейных уравнений с двумя переменными.

3) Назови методы решения систем линейных уравнений с двумя переменными.

4) Сформулируйте алгоритм решения по каждому способу решения в нескольких словах, назвав самое главное.

Этап № 7. Работа в парах

Сейчас мы с вами будем работать в парах: 1 вариант решает №12.4, а 2вариант решает №12.3; после того как ответы будут получены, меняемся тетрадями и проверяем ход решения соседа. Если все верно ставим +, если нет — (взаимопроверка с помощью мультимедиа)

Ответ: (3;-20).

Ответ: (5;2).

Этап № 7. Закрепление изученного материала:

Для закрепления изученного материала, давайте отгадаем крассворд.

1.Зависимость, в которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется…

Что является графиком линейного уравнения с двумя переменными?

Как называется график функции у=х 2 ?

Равенство, верное при любых значениях переменных, называется…

Произведение нескольких сомножителей, один из которых числовой, а другие – переменные и их степени, называется…

Сумма нескольких одночленов называется…

Как называются уравнения, имеющие одни и те же корни?

Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, называются…

Как называется функция, которую можно задать формулой у=кх+в, где х – независимая переменная, к, в – некоторые числа?

Этап № 8. Рефлексия :

Найдите своё место на горе.

Учащимся предлагается рисунок, на котором нужно отметить свое место положение для данного урока, т.е.:

Если мало чего понятного и придется разбираться ещё раз с этим материалом, то вы у подножья горы;

Если все предельно понятно, но вы не уверены в своих силах, то вы на пути к вершине;

Если нет ни каких вопросов, и вы чувствуете власть над данной темой, то вы на пике.

Источник

Решение систем линейных уравнений способом подстановки

Урок 42. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом подстановки»

· показать еще один способ решения систем линейных уравнений – способ подстановки.

На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1. выразить из какого-нибудь уравнения системы одну переменную через другую;

2. подставить вместо этой переменной полученное выражение в другое уравнение системы;

3. решить получившееся уравнение с одной переменной;

4. найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.

Источник