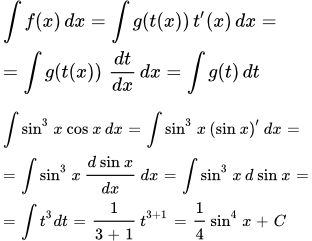Способ подстановки замены переменных для интегралов

Интегрирование методом замены переменной

Метод замены переменной

С помощью замены переменной можно вычислить простые интегралы и, в некоторых случаях, упростить вычисление более сложных.

Метод замены переменной заключается в том, что мы от исходной переменной интегрирования, пусть это будет x , переходим к другой переменной, которую обозначим как t . При этом мы считаем, что переменные x и t связаны некоторым соотношением x = x ( t ) , или t = t ( x ) . Например, x = ln t , x = sin t , t = 2 x + 1 , и т.п. Нашей задачей является подобрать такую зависимость между x и t , чтобы исходный интеграл либо свелся к табличному, либо стал более простым.

Основная формула замены переменной

Рассмотрим выражение, которое стоит под знаком интеграла. Оно состоит из произведения подынтегральной функции, которую мы обозначим как f ( x ) и дифференциала dx : . Пусть мы переходим к новой переменной t , выбрав некоторое соотношение x = x ( t ) . Тогда мы должны выразить функцию f ( x ) и дифференциал dx через переменную t .

Чтобы выразить подынтегральную функцию f ( x ) через переменную t , нужно просто подставить вместо переменной x выбранное соотношение x = x ( t ) .

Преобразование дифференциала выполняется так:
.
То есть дифференциал dx равен произведению производной x по t на дифференциал dt .

На практике, чаще всего встречается случай, в котором мы выполняем замену, выбирая новую переменную как функцию от старой: t = t ( x ) . Если мы догадались, что подынтегральную функцию можно представить в виде
,
где t′ ( x ) – это производная t по x , то
.

Итак, основную формулу замены переменной можно представить в двух видах.
(1) ,
где x – это функция от t .
(2) ,
где t – это функция от x .

Важное замечание

В таблицах интегралов переменная интегрирования, чаще всего, обозначается как x . Однако стоит учесть, что переменная интегрирования может обозначаться любой буквой. И более того, в качестве переменной интегрирования может быть какое-либо выражение.

В качестве примера рассмотрим табличный интеграл
.

Здесь x можно заменить любой другой переменной или функцией от переменной. Вот примеры возможных вариантов:
;
;
.

В последнем примере нужно учитывать, что при переходе к переменной интегрирования x , дифференциал преобразуется следующим образом:
.
Тогда
.

В этом примере заключена суть интегрирования подстановкой. То есть мы должны догадаться, что
.
После чего интеграл сводится к табличному.
.

Можно вычислить этот интеграл с помощью замены переменной, применяя формулу (2). Положим t = x 2 + x . Тогда
;
;

.

Примеры интегрирования заменой переменной

1) Вычислим интеграл
.
Замечаем, что (sin x )′ = cos x . Тогда

.
Здесь мы применили подстановку t = sin x .

2) Вычислим интеграл
.
Замечаем, что . Тогда

.
Здесь мы выполнили интегрирование заменой переменной t = arctg x .

3) Проинтегрируем
.
Замечаем, что . Тогда

. Здесь, при интегрировании, произведена замена переменной t = x 2 + 1 .

Линейные подстановки

Пожалуй, самыми распространенными являются линейные подстановки. Это замена переменной вида
t = ax + b ,
где a и b – постоянные. При такой замене дифференциалы связаны соотношением
.

Примеры интегрирования линейными подстановками

B) Найти интеграл
.
Решение.
Воспользуемся свойствами показательной функции.
.
ln 2 – это постоянная. Вычисляем интеграл.

.

C) Вычислить интеграл
.
Решение.
Приведем квадратный многочлен в знаменателе дроби к сумме квадратов.
.
Вычисляем интеграл.

.

D) Найти интеграл
.
Решение.
Преобразуем многочлен под корнем.

.
Интегрируем, применяя метод замены переменной .

.
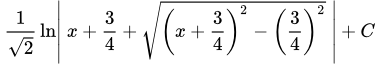
Ранее мы получили формулу
.
Отсюда
.
Подставив это выражение, получим окончательный ответ.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 06-09-2015

Источник

Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Сайт:	Навчальний сайт ХНАДУ
Курс:	Вища Математика (2 семестр) Вишневецький А.Л.
Книга:	Лекция 2. Замена переменной и и интегрирование по частям в неопределенном интеграле

Надруковано:	Гість
Дата:	четвер 18 листопад 2021 08:13

Зміст

Тема 1. Неопределенный интеграл, его свойства

1. Первообразная

Пусть f ( x ) – данная функция.

Определение . Функция F ( x ) называется первообразной для f ( x ) , если

Примеры . x 2 – первообразная для 2 x , т.к. ( x 2 )’ = 2 x . Впрочем, x 2 + 1 и x 2 — 5 – тоже первообразные для 2 x , т.к. ( x 2 + 1)’ = 2 x и ( x 2 — 5)’ = 2 x .

Теорема 1. Если F ( x ) – первообразная для f ( x ) , то

1) F ( x ) + С – тоже первообразная для f ( x ) .

2) Любая первообразная для f ( x ) имеет вид F ( x ) + С для некоторого С.

2. Неопределенный интеграл

Определение . Множество всех первообразных функции f ( x ) называется неопределенным интегралом от этой функции и обозначается так:

Здесь f ( x) dx – подынтегральное выражение, f ( x ) – подынтегральная функция, x – переменная интегрирования.

Если функция непрерывна на некотором отрезке, то на этом отрезке существует её неопределенный интеграл.

Операции нахождения дифференциала и неопределенного интеграла – взаимно обратные:

3. Свойства неопределенного интеграла

Формул «интеграл от произведения» и «интеграл от частного» функций нет.

4. Таблица первообразных

Таблица проверяется с помощью (1). Формулы № 10, 12, 14 есть обобщение формул № 9, 11, 13. В формулах № 10, 12, 14, 15 a ≠ 0 .

Полная запись формулы №1:

Тема 2. Основные методы интегрирования

5. Интегрирование подстановкой (заменой переменной)

Суть метода: путем введения новой переменной интегрирования (т.е. подста­новки) свести данный интеграл к более простому (желательно – к табличному).

Начнем с формулы замены. Надо найти интеграл

Сделаем подстановку φ(t) = x , где φ(t) — функция, имеющая непрерывную производную. По определению дифференциала, dx = φ'(t)dt . Подставляем в (1):

– формула замены переменной в неопределенном интеграле. После ее примене­ния и вычисления полученного интеграла нужно вернуться к исходной перемен­ной. Формулу (2) применяют как «слева направо», так и «справа налево». Общих методов подбора подстановок не существует.

6. Интегрирование по частям

Теорема . Если функции u = u(x) , ν = ν (x) имеют непрерывные производные, то

Док-во . Интегрируя равенство d(uv) = udv + vdu , получим uv = ∫ udv — ∫ vdu , т.е. (5)

Формула (5) сводит нахождение ∫ udv к нахождению ∫ vdu , поэтому ее приме­няют тогда, когда последний интеграл не сложнее первого. Для применения этой формулы подынтегральное выражение представляют как произведение двух сомножителей, один из которых обозначают u , другой dv . Затем u дифференцируют (находят du ), а dv интегрируют (находят v ).

Укажем способ выбора u и dv в двух типичных случаях. Пусть P(x) – многочлен.

Формулу (5) можно применять повторно. Например, в случае а) это делают n раз, где n – степень многочлена P(x) .

7. Интегрирование простейших рациональных дробей

Простейшие рациональные дроби – это дроби:

1 рода: ( k N ) и 2 рода: (дискриминант знаменателя D n = 1 так:

• Заменить

• Разложить интеграл в сумму вида

К первому интегралу применить формулу (4), а второй – табличный (арктангенс).

Источник

Замена переменной в неопределенном интеграле

Замена переменной в неопределенном интеграле используется при нахождении интегралов, в которых одна из функций является производной другой функции. Пусть есть интеграл $ \int f(x) dx $, сделаем замену $ x=\phi(t) $. Отметим, что функция $ \phi(t) $ является дифференцируемой, поэтому можно найти $ dx = \phi'(t) dt $.

Теперь подставляем $ \begin x = \phi(t) \\ dx = \phi'(t) dt \end $ в интеграл и получаем, что:

$$ \int f(x) dx = \int f(\phi(t)) \cdot \phi'(t) dt $$

Эта и есть формула замены переменной в неопределенном интеграле.

Алгоритм метода замены переменной

Таким образом, если в задаче задан интеграл вида: $$ \int f(\phi(x)) \cdot \phi'(x) dx $$ Целесообразно выполнить замену переменной на новую: $$ t = \phi(x) $$ $$ dt = \phi'(t) dt $$

После этого интеграл будет представлен в виде, который легко взять основными методами интегрирования: $$ \int f(\phi(x)) \cdot \phi'(x) dx = \int f(t)dt $$

Не нужно забывать также вернуть замененную переменную назад к $ x $.

Примеры решений

Найти неопределенный интеграл методом замены переменной: $$ \int e^ <3x>dx $$

Выполняем замену переменной в интеграле на $ t = 3x, dt = 3dx $:

$$ \int e^ <3x>dx = \int e^t \frac

<3>= \frac<1> <3>\int e^t dt = $$

Интеграл экспоненты всё такой же по таблице интегрирования, хоть вместо $ x $ написано $ t $:

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ $$ \int e^ <3x>dx = \frac<1> <3>e^ <3x>+ C $$

Найти неопределенный интеграл методом замены переменной:

$$ \int \sin^5 x \cos x dx $$

Замечаем, что $ (\sin x)’ = \cos x $, поэтому выгодно сделать замену переменной $$ t = \sin x, dt = \cos x dx $$

Тогда после подставления её в интеграл будем иметь:

$$ \int t^5 dt = \frac <6>+ C = \frac<1> <6>\sin x + C $$

В самом конце очень важно не забывать возвращать замену назад, чтобы получить окончательный ответ.

Пример 2

Ответ

$$ \int \sin^5 x \cos x dx =\frac<1><6>\sin x + C $$

Как обычно анализируем интеграл и замечаем, что в интеграле есть функция и её производная. А именно этой функцией является $ \sqrt $ и её производная $ \frac<1><2\sqrt> $. Поэтому замену переменной сделаем такой: $$ t = \sqrt, dt = \frac<2\sqrt> $$

Подставляем в интеграл и решаем:

$$ \int \frac<\cos \sqrt><\sqrt> dx = 2\int \cos t = 2\sin t + C = $$

Источник

Интегрирование: метод замены переменного, метод подстановки, интегрирование по частям

Вы будете перенаправлены на Автор24

Совокупность всех первообразных заданной функции $y=f(x)$, определенной на некотором отрезке, называется неопределенным интегралом от заданной функции $y=f(x)$. Неопределенный интеграл обозначается символом $\int f(x)dx $.

Определение 2 можно записать следующим образом:

Интегрирование функции $y=f(x)$ — это операция нахождения первообразной от заданной функции $y=f(x)$ (неопределенного интеграла заданной функции $y=f(x)$).

Операция интегрирования функции является обратной для операции дифференцирования.

Существуют различные методы вычисления неопределенного интеграла, например:

• подстановка (замена переменной);
• интегрирование по частям;
• и т.д.

Замена переменной (подстановка) — это один из способов вычисления неопределенного интеграла.

Суть метода подстановки заключается в том, что в интеграл вводится новая переменная интегрирования или делается подстановка. В результате чего исходный интеграл сводится либо к некоторому табличному интегралу, либо к интегралу, который к нему сводится.

После вычисления интеграла по новой переменной $t$ нужно обязательно возвратиться к первоначальной переменной $x$.

Пусть дан интеграл $\int f(x)dx $.

Сделаем следующую подстановку $x=\phi (t)$, при этом функция $\phi (t)$ дифференцируема.

\[dx=d\left(\phi (t)\right)=\phi ‘(t)dt.\]

Исходный интеграл будет иметь вид:

\[\int f(x)dx =\int f\left(\phi (t)\right)\cdot \phi ‘(t)dt .\]

Полученную формулу называют формулой замены переменной в неопределенном интеграле.

Готовые работы на аналогичную тему

Иногда целесообразнее делать замену не в виде $x=\phi (t)$, а в виде $t=\psi (x)$.

Проиллюстрировать замечание 2 при нахождении интеграла $\int \frac<\psi '(x)dx> <\psi (x)>$.

Сделаем замену $\psi (x)=t$.

Дифференцируя, получим $\psi ‘(x)dx=dt$.

Вычислим исходный интеграл:

Вычислить следующий интеграл: $\int \sqrt <\sin x>\cdot \cos xdx $

Сделаем подстановку: $t=\sin x$.

Тогда: $dt=\cos xdx$.

Подставим в исходный интеграл:

Интегрирование по частям — это один из способов вычисления неопределенного интеграла.

Суть метода заключается в том, что если подынтегральную функцию можно представить в виде произведения двух непрерывных функций в месте со своей производной (каждая из которых может быть как элементарной функцией, так и композицией элементарных), то справедлива следующая формула:

\[\int udv =uv-\int vdu .\]

Полученную формулу называют формулой интегрирования по частям.

При нахождении функции $v$ путем интегрирования выражения $dv$, константу $C$ можно считать равной нулю.

Рассмотрим функции $u=u(x),\, \, v=v(x)$, имеющие непрерывные производные. По свойствам дифференциалов, справедливо следующее равенство:

Проинтегрировав левую часть и правую часть последнего равенства, получим:

\[\int d(uv) =\int udv+vdu \Rightarrow uv=\int udv +\int vdu \]

Полученное равенство можно переписать в виде:

\[\int udv =uv-\int vdu \]

Вычислить следующий интеграл: $\int x\cdot e^ dx $.

Полагая $u=x,dv=e^ dx$, получим $du=dx,v=\int e^ dx =e^ $.

По соответствующей формуле получим:

\[\int x\cdot e^ dx =x\cdot e^ -\int e^ dx =x\cdot e^ -e^ +C\]

\[\int x\cdot e^ dx =x\cdot e^ -e^ +C.\]

Иногда для вычисления сложных интегралов формула интегрирования по частям используется несколько раз.

Формулу интегрирования по частям имеет смысл применять при вычислении интегралов следующего вида:

• $\int P_ (x)\cdot e^ dx ;\int P_ (x)\cdot \sin (kx)dx ;\int P_ (x)\cdot \cos (kx)dx $, где $P_ (x)$ — это многочлен степени $n$, $k=const$;
• $\int P_ (x)\cdot \ln xdx ;\int P_ (x)\cdot \arcsin (kx)dx ;\int P_ (x)\cdot \arccos (kx)dx $;
• $\int e^ \cdot \sin (cx+f)dx ;\int e^ \cdot \cos (cx+f)dx $

В первом случае в качестве функции $u$ выбирается многочлен $P_ (x)$, в качестве $dv$ — оставшиеся под знаком интеграла множители. Для интеграла подобного вида формула интегрирования по частям применяется $n$ раз.

Во втором случае в качестве $dv$ выбирается $dv=P_ (x)dx$, а в качестве функции $u$ — оставшиеся сомножители.

В третьем случае в качестве функции $u$ выбирается либо экспонента, либо тригонометрическая функция. При повторном применении формулы интегрирования по частям в качестве функции $u$ выбирается та же функция (экспонента либо тригонометрическая функция соответственно).

Вычислить следующий интеграл: $\int x\cdot \sin (2x)dx $

Полагая $u=x,dv=\sin 2xdx$, получим $du=dx,v=\int \sin 2xdx =\frac<1> <2>\int \sin 2xd(2x) =-\frac<1> <2>\cos 2x$.

По соответствующей формуле получим:

\[\int x\cdot \sin (2x)dx =-\frac<1> <2>x\cdot \cos 2x+\frac<1> <4>\sin 2x+C.\]

Вычислить следующий интеграл: $\int x\cdot \ln xdx $

Полагая $u=\ln x,dv=xdx$, получим $du=\frac ,v=\int xdx =\frac > <2>$.

По соответствующей формуле получим:

\[\int x\cdot \ln xdx =\ln x\cdot \frac > <2>-\int \frac > <2>\cdot \frac =\ln x\cdot \frac > <2>-\frac<1> <2>\int xdx =\ln x\cdot \frac > <2>-\frac > <4>+C.\]

\[\int x\cdot \ln xdx =\ln x\cdot \frac > <2>-\frac > <4>+C.\]

Вычислить следующий интеграл: $\int e^ \cdot \sin xdx $

Полагая $u=\sin x,dv=e^ dx$, получим $du=\cos xdx,v=\int e^ dx =e^ $.

Используя формулу, получим:

\[\int \sin x\cdot e^ dx =\sin x\cdot e^ -\int e^ \cdot \cos xdx .\]

Пусть $u_ <1>=\cos x,dv_ <1>=e^ dx$, тогда $du_ <1>=-\sin xdx,v_ <1>=\int e^ dx =e^ $.

По соответствующей формуле получим:

\[\begin <\int \sin x\cdot e^dx =\sin x\cdot e^ -\int e^ \cdot \cos xdx =\sin x\cdot e^ -\left(\cos x\cdot e^ +\int e^ \cdot \sin xdx \right)=\sin x\cdot e^ -> \\ <-\cos x\cdot e^-\int e^ \cdot \sin xdx > \end.\]

Выразим исходный интеграл:

\[\int \sin x\cdot e^ dx =\sin x\cdot e^ -\cos x\cdot e^ -\int e^ \cdot \sin xdx ;\] \[2\int \sin x\cdot e^ dx =\sin x\cdot e^ -\cos x\cdot e^ ;\] \[\int \sin x\cdot e^ dx =\frac<1> <2>\cdot \left(\sin x\cdot e^ -\cos x\cdot e^ \right)+C.\]

\[\int \sin x\cdot e^ dx =\frac<1> <2>\cdot \left(\sin x\cdot e^ -\cos x\cdot e^ \right)+C.\]

Источник

Читайте также:  Работа это способ передачи внутренней энергии

Оцените статью

Вам также может понравиться

Ясень семена способ распространения

Ясень обыкновенный Fraxinus excelsior – так в ботанической

Ярлыки способы создания ярлыков ос windows

Создаем ярлыки на рабочем столе Windows Создаем ярлыки

Японское удобрение фуджима способ применения

Удобрения Фуджима Знаете потрясающее удобрение, палочка

Японский чай способ заварки

Технология заваривания японского чая Известно, что

• Правообладателям
• Политика конфиденциальности
• Контакты

Пример 3

Найти интеграл с помощью замены переменной: $$ \int \frac<\cos \sqrt><\sqrt> dx $$

Решение