Шифрование методом замены (подстановки)



Шифр подстановки – это метод шифрования, в котором элементы исходного открытого текста заменяются зашифрованным текстом в соответствии с некоторым правилом. Элементами текста могут быть отдельные символы (самый распространённый случай), пары букв, тройки букв, комбинирование этих случаев и так далее. В классической криптографии различают четыре типа шифра подстановки[8]:
- Одноалфавитный шифр подстановки (шифр простой замены) — шифр, при котором каждый символ открытого текста заменяется на некоторый, фиксированный при данном ключе символ того же алфавита.
- Однозвучный шифр подстановки похож на одноалфавитный за исключением того, что символ открытого текста может быть заменен одним из нескольких возможных символов.
- Полиграммный шифр подстановки заменяет не один символ, а целую группу. Примеры: шифр Плейфера, шифр Хилла.
- Полиалфавитный шифр подстановки состоит из нескольких шифров простой замены. Примеры: шифр Виженера, шифр Бофора, одноразовый блокнот.
В качестве альтернативы шифрам подстановки можно рассматривать перестановочные шифры. В них, элементы текста переставляются в ином от исходного порядке, а сами элементы остаются неизменными. Напротив, в шифрах подстановки, элементы текста не меняют свою последовательность, а изменяются сами.
Шифры простой замены
В шифрах простой замены замена производится только над одним-единственным символом. Для наглядной демонстрации шифра простой замены достаточно выписать под заданным алфавитом тот же алфавит, но в другом порядке или, например, со смещением. Записанный таким образом алфавит называют алфавитом замены.
Шифр простой замены Атбаш [9], использованный для еврейского алфавита и получивший оттуда свое название. Шифрование происходит заменой первой буквы алфавита на последнюю, второй на предпоследнюю и т.д. Шифр Атбаш для английского алфавита:
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | Z Y X W V U T S R Q P O N M L K J I H G F E D C B A |
Шифр Цезаря — один из древнейших шифров. При шифровании каждая буква заменяется другой, отстоящей от ней в алфавите на фиксированное число позиций. Шифр назван в честь римского императора Гая Юлия Цезаря, использовавшего его для секретной переписки.
Общая формула шифра Цезаря имеет следующий вид:
| С=P+K (mod M), | (4.1) |
где P – номер символа открытого текста, С – соответствующий ему номер символа шифротекста, K – ключ шифрования (коэффициент сдвига), M – размер алфавита (для русского языка M = 32)
Для данного шифра замены можно задать фиксированную таблицу подстановок, содержащую соответствующие пары букв открытого текста и шифротекста.
Пример 4.1 . Таблица подстановок для символов русского текста при ключе K=3 представлена в таблице 4.1. Данной таблице соответствует формула:
| С=P+3 (mod 32) | (4.2) |
Табл. 4.1. Табл. подстановок шифра Цезаря для ключа K=3
| А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П |
| Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т |
| Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я |
| У | Ф | Х | Ц | Ч | Ш | Щ | Ъ | Ы | Ь | Э | Ю | Я | А | Б | В |
Согласно формуле (4.2) открытый текст «БАГАЖ» будет преобразован в шифротекст «ДГЖГЙ».
Дешифрование закрытого текста, зашифрованного методом Цезаря согласно (4.1), осуществляется по формуле:
| P=C-K (mod M) | (4.3) |
Естественным развитием шифра Цезаря стал шифр Виженера. Например, шифрование с использованием ключа 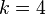
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | E F G H I J K L M N O P Q R S T U V W X Y Z A B C D |
Современным примером шифра Цезаря является ROT13. Он сдвигает каждый символ английского алфавита на 13 позиций. Используется в интернет-форумах, как средство для сокрытия основных мыслей, решений загадок и пр. [9].
Шифр с использованием кодового слова является одним из самых простых как в реализации, так и в расшифровывании. Идея заключается в том, что выбирается кодовое слово, которое пишется впереди, затем выписываются остальные буквы алфавита в своем порядке. Шифр с использованием кодового слова WORD.
| Исходный алфавит: | A B C D E F G H I J K L M N O P Q R S T U V W X Y Z |
| Алфавит замены: | W O R D A B C E F G H I J K L M N P Q S T U V X Y Z |
Как мы видим, при использовании короткого кодового слова мы получаем очень и очень простую замену. Также мы не можем использовать в качестве кодового слова слова с повторяющимися буквами, так как это приведет к неоднозначности расшифровки, то есть двум различным буквам исходного алфавита будет соответствовать одна и та же буква шифрованного текста. Слово COD будет преобразованно в слово RLD [10].

Шифр простой моноалфавитной замены является обобщением шифра Цезаря и выполняет шифрование по следующей схеме:
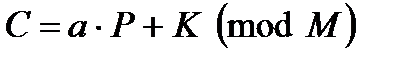 , , | (4.4) |
где 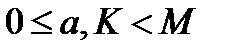
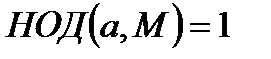
Пусть M=26, a=3, K=6, НОД(3,26) = 1. Тогда получаем следующую таблицу подстановок для шифра простой моноалфавитной замены.
Табл. 4.2. Табл. подстановок для шифра моноалфавитной замены.
| A | B | C | D | E | F | G | H | I | G | K | L | M | N | O | P | Q | R | S |
| P | ||||||||||||||||||
| C | ||||||||||||||||||
| T | U | V | W | X | Y | Z | ||||||||||||
| P | ||||||||||||||||||
| C |
Тогда открытый текст «HOME» будет преобразован в шифротекст «BWQS».
Дешифрование текста «BWQS» выполняем в порядке обратном шифрованию, т.е. смотрим у буквы В ее номер Р обозначим его через 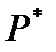
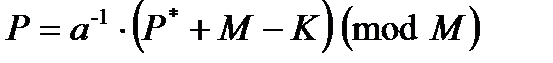 | (4.5) |
Шифр Гронсфельда. Данный шифр представляет собой модификацию шифра Цезаря с числовым ключом. При реализации данного шифра под буквами исходного сообщения записывают цифры числового ключа. Если ключ короче сообщения, то его запись циклически повторяют. Получение символа шифротекста осуществляют также, как это делается в шифре Цезаря, при этом смещение символа открытого текста производят на количество позиций, соответствующего цифре ключа, стоящей под ним.
Пусть необходимо зашифровать исходное сообщение «НОЧЕВАЛА ТУЧКА ЗОЛОТАЯ», в качестве ключа возьмем К=193431.
Табл. 4.3. Табл. подстановок шифра Гронсфельда для ключа K=193431
| Сообщение | Н | О | Ч | Е | В | А | Л | А | Т | У | Ч | К | А | З | О | Л | О | Т | А | Я |
| Ключ | ||||||||||||||||||||
| Шифро- текст | О | Ч | Ь | Й | Е | Б | М | Й | Х | Ч | Ь | Л | Б | Р | С | П | С | У | Б | И |
Для того, чтобы зашифровать первую букву сообщения Н, необходимо сдвинуть ее в алфавите русских букв на число позиций, соответствующее цифре ключа, т.е. на 1, в результате чего получим букву О.
Дешифрование шифротекста предполагает сдвиг его символов на необходимое число позиций в обратную сторону.
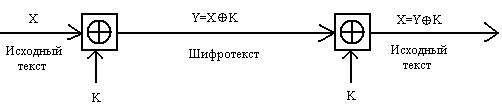
Шифрование методом Вернама
При шифровании открытого текста, каждый его символ представляется в двоичном виде [3]. Ключ шифрования также представляется в двоичной форме. Шифрование исходного текста осуществляется путем сложения по модулю 2 двоичных символов открытого текста с двоичными символами ключа:
Дешифрование состоит в сложении по модулю 2 символов шифротекста с ключом.
Рис. 4.2. Схема системы шифрования Вернама
Модификация системы шифрования Вернама используется для криптографической защиты информации в архиваторе ARJ. Формула (4.6) в этом случае принимает следующий вид:
| Y=PÅ(K+VALUE), | (4.7) |
где VALUE – фиксированное значение.
Пример 4.4. Зашифруем с помощью системы Вернама открытый текст «БЛАНК» с помощью ключа «ОХ».
Преобразуем открытый текст «БЛАНК» в ASCII коды: Б=129, Л=139, A=128, Н=141, К=138. В двоичном виде последовательность 129, 139, 128, 141, 138 представится в виде 10000001 10001011 10000000 10001101 10001010.
Табл. 4.4. Двоичные коды слова БЛАНК
| символ | код | 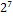 | 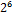 | 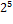 | 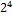 | 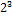 | 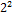 | 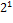 | 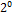 |
| Б | |||||||||
| Л | |||||||||
| А | |||||||||
| Н | |||||||||
| К |
Преобразуем ключ «ОХ» в ASCII коды: О=142, Х=149. В двоичном виде последовательность 142, 149 представится в виде 10001110 10010101.
Подпишем циклически ключ под открытым текстом и выполним сложение по модулю 2 соответствующих битов.
Источник
Простейшие методы шифрования с закрытым ключом
Методы замены
Методы шифрования заменой (подстановкой) основаны на том, что символы исходного текста, обычно разделенные на блоки и записанные в одном алфавите, заменяются одним или несколькими символами другого алфавита в соответствии с принятым правилом преобразования.
Одноалфавитная замена
Одним из важных подклассов методов замены являются одноалфавитные (или моноалфавитные) подстановки, в которых устанавливается однозначное соответствие между каждым знаком ai исходного алфавита сообщений A и соответствующим знаком ei зашифрованного текста E . Одноалфавитная подстановка иногда называется также простой заменой, так как является самым простым шифром замены.
Примером одноалфавитной замены является шифр Цезаря, рассмотренный ранее. В рассмотренном в «Основные понятия криптографии» примере первая строка является исходным алфавитом, вторая (с циклическим сдвигом на k влево) – вектором замен.
В общем случае при одноалфавитной подстановке происходит однозначная замена исходных символов их эквивалентами из вектора замен (или таблицы замен). При таком методе шифрования ключом является используемая таблица замен.
Подстановка может быть задана с помощью таблицы, например, как показано на рис. 2.3.
В таблице на рис. 2.3 на самом деле объединены сразу две таблицы. Одна (шифр 1) определяет замену русских букв исходного текста на другие русские буквы, а вторая (шифр 2) – замену букв на специальные символы. Исходным алфавитом для обоих шифров будут заглавные русские буквы (за исключением букв » Ё » и » Й «), пробел и точка.
Зашифрованное сообщение с использованием любого шифра моноалфавитной подстановки получается следующим образом. Берется очередной знак из исходного сообщения. Определяется его позиция в столбце «Откр. текст» таблицы замен. В зашифрованное сообщение вставляется шифрованный символ из этой же строки таблицы замен.
Попробуем зашифровать сообщение «ВЫШЛИТЕ ПОДКРЕПЛЕНИЕ» c использованием этих двух шифров ( рис. 2.4). Для этого берем первую букву исходного сообщения «В» . В таблице на рис. 2.3 в столбце «Шифр 1» находим для буквы «В» заменяемый символ. Это будет буква «О» . Записываем букву «О» под буквой «В» . Затем рассматриваем второй символ исходного сообщения – букву «Ы» . Находим эту букву в столбце «Откр. текст» и из столбца «Шифр 1» берем букву, стоящую на той же строке, что и буква «Ы» . Таким образом получаем второй символ зашифрованного сообщения – букву «Н» . Продолжая действовать аналогично, зашифровываем все исходное сообщение ( рис. 2.4).
Полученный таким образом текст имеет сравнительно низкий уровень защиты, так как исходный и зашифрованный тексты имеют одинаковые статистические закономерности. При этом не имеет значения, какие символы использованы для замены – перемешанные символы исходного алфавита или таинственно выглядящие знаки.
Зашифрованное сообщение может быть вскрыто путем так называемого частотного криптоанализа. Для этого могут быть использованы некоторые статистические данные языка, на котором написано сообщение.
Известно, что в текстах на русском языке наиболее часто встречаются символы О, И . Немного реже встречаются буквы Е, А . Из согласных самые частые символы Т, Н, Р, С . В распоряжении криптоаналитиков имеются специальные таблицы частот встречаемости символов для текстов разных типов – научных, художественных и т.д.
Криптоаналитик внимательно изучает полученную криптограмму, подсчитывая при этом, какие символы сколько раз встретились. Вначале наиболее часто встречаемые знаки зашифрованного сообщения заменяются, например, буквами О . Далее производится попытка определить места для букв И, Е, А . Затем подставляются наиболее часто встречаемые согласные. На каждом этапе оценивается возможность «сочетания» тех или иных букв. Например, в русских словах трудно найти четыре подряд гласные буквы, слова в русском языке не начинаются с буквы Ы и т.д. На самом деле для каждого естественного языка (русского, английского и т.д.) существует множество закономерностей, которые помогают раскрыть специалисту зашифрованные противником сообщения.
Возможность однозначного криптоанализа напрямую зависит от длины перехваченного сообщения. Посмотрим, с чем это связано. Пусть, например, в руки криптоаналитиков попало зашифрованное с помощью некоторого шифра одноалфавитной замены сообщение:
Это сообщение состоит из 11 символов. Пусть известно, что эти символы составляют целое сообщение, а не фрагмент более крупного текста. В этом случае наше зашифрованное сообщение состоит из одного или нескольких целых слов. В зашифрованном сообщении символ Ъ встречается 2 раза. Предположим, что в открытом тексте на месте зашифрованного знака Ъ стоит гласная О, А, И или Е . Подставим на место Ъ эти буквы и оценим возможность дальнейшего криптоанализа таблица 2.1
| Зашифрованное сообщение | ||||||||||
| Т | Н | Ф | Ж | . | И | П | Щ | Ъ | Р | Ъ |
| После замены Ъ на О | ||||||||||
| О | О | |||||||||
| После замены Ъ на А | ||||||||||
| А | А | |||||||||
| После замены Ъ на И | ||||||||||
| И | И | |||||||||
| После замены Ъ на Е | ||||||||||
| Е | Е | |||||||||
Все приведенные варианты замены могут встретиться на практике. Попробуем подобрать какие-нибудь варианты сообщений, учитывая, что в криптограмме остальные символы встречаются по одному разу ( таблица 2.2).
| Зашифрованное сообщение | ||||||||||
| Т | Н | Ф | Ж | . | И | П | Щ | Ъ | Р | Ъ |
| Варианты подобранных дешифрованных сообщений | ||||||||||
| Ж | Д | И | С | У | М | Р | А | К | А | |
| Д | Ж | О | Н | А | У | Б | И | Л | И | |
| В | С | Е | Х | П | О | Б | И | Л | И | |
| М | Ы | П | О | Б | Е | Д | И | Л | И | |
Кроме представленных на таблица 2.2 сообщений можно подобрать еще большое количество подходящих фраз. Таким образом, если нам ничего не известно заранее о содержании перехваченного сообщения малой длины, дешифровать его однозначно не получится.
Если же в руки криптоаналитиков попадает достаточно длинное сообщение, зашифрованное методом простой замены, его обычно удается успешно дешифровать. На помощь специалистам по вскрытию криптограмм приходят статистические закономерности языка. Чем длиннее зашифрованное сообщение, тем больше вероятность его однозначного дешифрования.
В «Алгоритм криптографического преобразования данных ГОСТ 28147-89» будут более подробно рассмотрены вопросы теоретической стойкости криптосистем, а также принципы построения идеальных криптосистем.
Интересно, что если попытаться замаскировать статистические характеристики открытого текста, то задача вскрытия шифра простой замены значительно усложнится. Например, с этой целью можно перед шифрованием «сжимать» открытый текст с использованием компьютерных программ-архиваторов.
С усложнением правил замены увеличивается надежность шифрования. Можно заменять не отдельные символы, а, например, двухбуквенные сочетания – биграммы. Таблица замен для такого шифра может выглядеть, как на таблица 2.3.
| Откр. текст | Зашифр. текст | Откр. текст | Зашифр. текст |
|---|---|---|---|
| аа | кх | бб | пш |
| аб | пу | бв | вь |
| ав | жа | . | . |
| . | . | яэ | сы |
| ая | ис | яю | ек |
| ба | цу | яя | рт |
Оценим размер такой таблицы замен. Если исходный алфавит содержит N символов, то вектор замен для биграммного шифра должен содержать N 2 пар «откр. текст – зашифр. текст» . Таблицу замен для такого шифра можно также записать и в другом виде: заголовки столбцов соответствуют первой букве биграммы, а заголовки строк – второй, причем ячейки таблицы заполнены заменяющими символами. В такой таблице будет N строк и N столбцов ( таблица 2.4).
| а | б | . | я | |
|---|---|---|---|---|
| а | кх | цу | . | . |
| б | пу | пш | . | . |
| в | жа | вь | . | . |
| . | . | . | . | . |
| ю | . | . | . | ек |
| я | ис | . | . | рт |
Возможны варианты использования триграммного или вообще n-граммного шифра. Такие шифры обладают более высокой криптостойкостью, но они сложнее для реализации и требуют гораздо большего количества ключевой информации (большой объем таблицы замен). В целом, все n-граммные шифры могут быть вскрыты с помощью частотного криптоанализа, только используется статистика встречаемости не отдельных символов, а сочетаний из n символов.
Источник