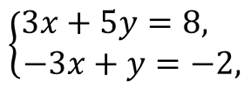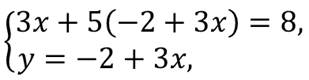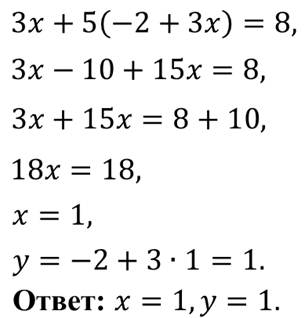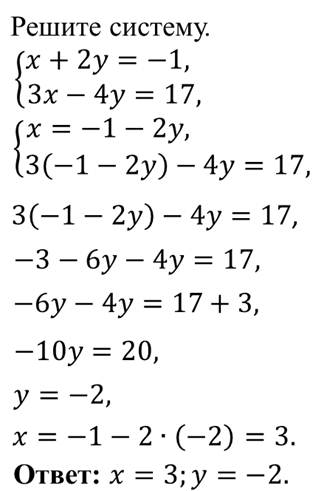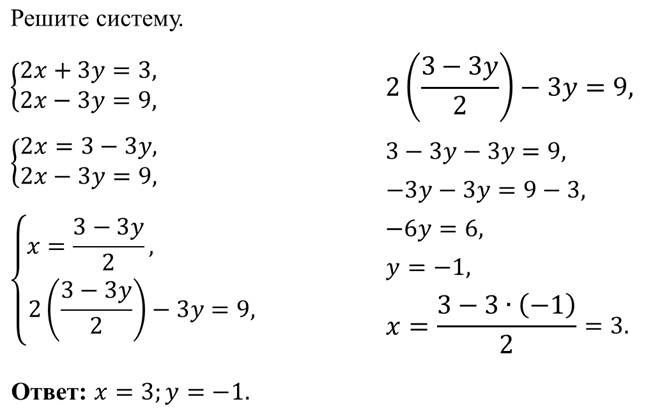Способ подстановки при решении систем линейных уравнений 7 класс

Решение систем линейных уравнений способом подстановки

Урок 42. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом подстановки»

· показать еще один способ решения систем линейных уравнений – способ подстановки.

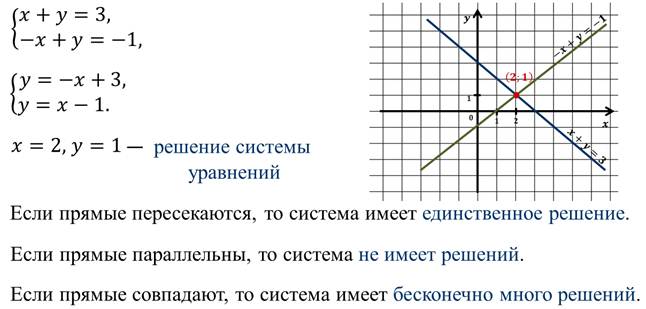
На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1. выразить из какого-нибудь уравнения системы одну переменную через другую;

2. подставить вместо этой переменной полученное выражение в другое уравнение системы;

3. решить получившееся уравнение с одной переменной;

4. найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.

Источник

Решение системы линейных уравнений методом подстановки

Алгоритм решения системы линейных уравнений методом подстановки

1. Из любого уравнения системы выразить одну переменную через другую.
2. Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
3. Решить второе уравнение относительно выраженной переменной.
4. Подставить найденное значение переменной в выражение, полученное на первом шаге.
5. Найти значение второй переменой.
6. Записать ответ в виде упорядоченной пары найденных значений переменных.

Из второго уравнения выражаем y:

Подставляем выражение для y в первое уравнение:

Шаг 3 Решаем первое уравнение:

Подставляем значение x в выражение для y:

В последовательной записи:

$$ <\left\< \begin 3x+y = 5 \\ y-x = 1 \end \right.> \Rightarrow <\left\< \begin 3x+y = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 3x+(x+1) = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 4x = 5-1 \\ y = x+1 \end \right.> \Rightarrow $$ $$ \Rightarrow <\left\< \begin x = 1 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 2\end \right.> $$

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) <\left\< \begin 5x-4y = 3 \\ 2x-3y = 4 \end \right.> \Rightarrow <\left\< \begin 5x-4y = 3 \\ x = \frac<3y+4> <2>= 1,5y+2 \end \right.> \Rightarrow <\left\< \begin 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7,5y+10-4y = 3 \\ x=1,5y+2 \end \right.> \Rightarrow <\left\< \begin 3,5y = -7 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin y = -2 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin x = -1 \\ y = -2\end \right.> $

$ б) <\left\< \begin 4x-3y = 7 \\ 3x-4y = 0 \end \right.> \Rightarrow <\left\< \begin 4x-3y = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin 4x-3\cdot \frac<3> <4>x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin (4- \frac<9><4>)x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 7 \cdot \frac<4> <7>= 4 \\ y = \frac<3> <4>x = \frac<3> <4>\cdot 4 = 3 \end \right.> \Rightarrow <\left\< \beginx = 4 \\ y = 3 \end \right.> $

$ в) <\left\< \begin 5a-4b = 9 \\ 2a+3b = -1 \end \right.> \Rightarrow <\left\< \begin 5a-4b = 9 \\ a = \frac<-3b-1> <2>= -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin-11,5b = 11,5 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin a = 1 \\ b = -1 \end \right.> $

$ г) <\left\< \begin 7a+4b = 5 \\ 3a+2b = 1 \end \right.> \Rightarrow <\left\< \begin 7a+4b = 5 \\ b = \frac<-3a+1> <2>= -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end \right.> $

Пример 2. Найдите решение системы уравнений:

$а) <\left\< \begin \frac<4>-y = 7 | \times 4 \\ 3x+ \frac <2>= 9 | \times 2\end \right.> \Rightarrow <\left\< \begin x-4y = 28 \\ 6x+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 4(y+7) \\ 24y+168+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4(y+7) \\ 25y = -150 \end \right.> \Rightarrow <\left\< \beginx = 4(-6+7) = 4 \\ y = -6 \end \right.>$

$ в) <\left\< \begin 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end \right.> \Rightarrow <\left\< \begin 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 10x-8y = -14 |:2 \\ x+8y = 25 \end \right.> \Rightarrow <\left\< \begin 5x-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin 5(-8y+25)-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -40y+125-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin -44y = -132 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 3 \end \right.> $

$ г) <\left\< \begin 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end \right.> \Rightarrow <\left\< \begin 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ 2x-6y = 4 |:2 \end \right.>$

$$ \Rightarrow <\left\< \begin 7x+22y = 57 \\ x-3y = 2 \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 7(3y+2)+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin 21y+14+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 43y = 43 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin x = 5 \\ y = 1 \end \right.>$$

Пример 3*. Найдите решение системы уравнений:

Перепишем систему и найдём решение для новых переменных:

$$ <\left\< \begin 3a+8b = 5 \\ 12b-a = 2 \end \right.> \Rightarrow <\left\< \begin 3(12b-2)+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow <\left\< \begin 36b-6+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow $$

Источник

Конспект урока алгебры в 7 классе по теме: «Решение систем линейных уравнений методом подстановки».

План – конспект урока по алгебре в 7-м классе на тему:

« Решение систем линейных уравнений способом подстановки »

Образовательные: – разобрать, в чем состоит способ подстановки решения систем линейных уравнений; вывести алгоритм применения этого способа; сформировать умение решать системы уравнений способом подстановки.

Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Развивающие: — развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала.

разобрать, в чем состоит способ подстановки решения систем линейных уравнений;

вывести алгоритм применения этого способа;

сформировать умение решать системы уравнений способом подстановки продолжить формирование мотивации обучающихся к изучению предмета,

развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе,

воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, учёбе;

воспитывать инициативу и самостоятельность в деятельности;

подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.

Тип урока: урок изучения новой темы.

Вид урока: комбинированный.

Оборудование: мультимедийный проектор, компьютер, презентация в программе Microsoft Office Power Point, учебник и задачник по алгебре.

1. Алгебра. 7 класс. В 2 ч., А. Г. Мордкович. Учебник и задачник для общеобразовательных учреждений – М. Мнемозина,2011 г

2. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 7 класс./ С.А. Пушкин, И.Л. Гусева. – М.: «Интеллект», 2013.

3. Т.Ю.Дюмина, А.А.Махонина, «Алгебра. Поурочные планы» — Волгоград: «Учитель», 2013 г.

Нацелить учащихся на урок

Актуализация опорных знаний.

Игра «Лови ошибку» (устная работа по повторению пройденного материала)

Проверка домашнего задания.

Разбор домашнего задания, выход на проблемный вопрос и мотивация к деятельности.

Изучение нового материала.

Ответ на проблемный вопрос, разбор нового метода решения систем с выведением алгоритма.

Закрепление изученного материала.

Отработка алгоритма решения системы линейных уравнений. Групповая работа. Фронтальная работа. Самостоятельная работа.

Подведение итогов урока.

Разъяснить содержание домашнего задания.

1. Организационный момент.

— Здравствуйте, ребята. Все готовы к уроку?

— Я хочу пожелать вам, чтобы сегодня у нас на уроке было хорошее рабочее настроение.

2. Актуализация опорных знаний. — Новые знания нам будет очень трудно осваивать без умения быстро и верно решать простейшие уравнения с одной переменной и умения выражать одну переменную через другую. Я предлагаю вам проверить, верно ли выполнены задания на слайдах ( Лови ошибку!)

Выразите в уравнениях переменную « у » через « х »:

у – 16х = 13 у =16х – 13

9х- 2у = 5 -2у = -9х+5 у =-4,5х +2,5

— Молодцы! Вы нашли все ошибки, и заодно повторили правила переноса слагаемых из одной части уравнения в другую.

2. Проверка домашнего задания.

— Переходим к проверке домашнего задания. Какую работу вы выполняли дома? (решали системы графическим методом)

— Давайте проверим ваши результаты. Посмотрите на слайды и сравните их со своим решением. (Слайды 1 и 2)

— В чём отличие первой системы от второй? (в первой координаты точки точно определились, а во второй нет)

— Как вы думаете, почему во второй системе у вас получились разные ответы? (были погрешности при построении, например плохо заточен карандаш, или неровно приложили линейку)

— Тогда логично будет задать вопрос: Всегда ли применим графический метод решения систем линейных уравнений? (Проблемный вопрос ) (нет).

— Но систему решить нужно, поэтому возникает потребность в другом методе решения систем. С таким методом мы познакомимся сегодня на уроке. Его название – Метод подстановки. Запишите в тетрадях число и тему урока: «Способ подстановки».

— Итак, на сегодняшнем уроке мы с вами познакомимся с методом подстановки для решения систем линейных уравнений, выведем алгоритм применения этого способа и научимся решать системы этим новым способом. Для этого на уроке вы должны быть собранными, внимательными, открытыми и доброжелательными.

4. Изучение нового материала.

Рассмотрим систему уравнений, которая вызвала у вас затруднения дома.

Давайте её решим. Для этого мы должны изучить алгоритм решения и пошагово следовать по каждому пункту алгоритма.

В чём же заключается этот метод? (Слайд)

Алгоритм решения системы уравнения методом подстановки.

Выразить одну переменную через другую в одном из уравнений системы.

Подставить полученное выражение в другое уравнение системы.

Решить полученное уравнение с одной переменной.

Найти значение другой переменной. (подставив, найденной значение)

Записать ответ в виде пары значений (х;у).

Учитель на доске показывает решение этой системы. Ученики записывают решение.

— Этим методом часто пользуются при решении систем на экзаменах!

— А сейчас давайте сделаем паузу. Встанем и разомнёмся.(выполняем несколько упражнений + гимнастика для глаз)

Закрепление изученного материала.

Решение системы из учебника.№12.8 (в) – один человек у доски с подробным комментированием каждого шага алгоритма, остальные в тетрадях.

Групповая работа. Класс разбивается на 5 групп по 4 человека. Каждая группа должна решить систему. При этом разрешается членам группы помогать друг другу, объяснять задание. Учитель оказывает также помощь по необходимости, наблюдает за ребятами. Далее учитель на слайде демонстрирует решение задания. Ребята проверяют свои данные с решениями на слайде.

Самостоятельная работа. В тетрадях ребята решают систему. Далее меняются тетрадями и проверяют друг друга. (резерв)

— О чём вы узнали на сегодняшнем уроке?

-В чём преимущества этого метода решения в отличие от графического метода?

Напомните алгоритм решения систем методом подстановки.

Учитель выставляет оценки за урок

Домашнее задание: Выучить алгоритм в пункте 12, №12.5, 12.3 (а), 12.8(а).

Рефлексия. Ребята, посмотрите на слайд и ответьте на представленные вопросы:

Доволен ли ты тем, как прошел урок?

Возникали ли проблемы при решении заданий?

Сможете ли вы самостоятельно выполнить домашнее задание?

И по результатам поднимите карточки, которые лежат на ваших столах.

— Я рада, что для вас урок прошёл с пользой. Мы обязательно будем разбирать этот метод на следующих уроках и на консультациях. И я надеюсь, что на региональном экзамене с этими заданиями справятся все. Урок окончен. Спасибо за внимание!

Источник