- Разрядные слагаемые
- Число по разрядам онлайн
- Как разложить натуральное число по разрядам
- Что такое разрядное слагаемое ?
- Классы чисел
- Разряды чисел
- Сумма разрядных слагаемых
- Сумма разрядных слагаемых
- Разряды и классы чисел
- Примеры
- Урок 11 Бесплатно Разложение числа по разрядам. Способы сложение натуральных чисел
- Разряды и классы
- Способы сложения натуральных чисел
Разрядные слагаемые
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых.
Например, число « 64 » состоит из 6 десятков и 4 единиц.
Числа « 60 » и « 4 » называются разрядными слагаемыми.
Представление числа в виде:
356 = 3 сотни + 5 десятков + 6 единиц = 3 · 100 + 5 · 10 + 6 = 300 + 50 + 6
8 092 = 8 тысяч + 0 сотен + 9 десятков + 2 единицы = 8 · 1 000 + 0 · 100 + 9 · 10 + 2 = 8 000 + 90 + 2
Числа 1, 10, 100, 1000 и т.д. — называются разрядными единицами. Так, 1 — это единица разряда единиц; 10 — единица разряда десятков; 100 — единица разряда сотен и т.д.
Часто в заданиях требуется не только разложить число на разрядные слагаемые, но и определить количество всех единиц какого-либо разряда. В этом случае советуем сделать подробный разбор числа.
Пример подробного разбора многозначного числа « 2 038 479 » (два миллиона тридцать восемь тысяч четыреста семьдесят девять).
- Вначале разложим число на сумму разрядных слагаемых.
2 038 479 = 2 · 1 000 000 + 0 · 100 000 + 3 · 10 000 + 8 · 1 000 + 4 · 100 +
+ 7 · 10 + 9 = 2 000 000 + 30 000 + 8 000 + 400 + 70 + 9
- Это число состоит из:
- двух единиц миллионов (2 · 1 000 000) ;
- трёх десятков тысяч (3 · 10 000) ;
- восьми единиц тысяч (8 · 1000) ;
- четырёх сотен (4 · 100) ;
- семи десятков (7 · 10) ;
- девяти единиц (9) .
- Определим сколько в числе « 2 038 479 » всего единиц с помощью таблицы.
| Сколько в числе всего единиц? Чтобы определить количество единиц, записываем всё число, включая сам разряд единиц. | 2 038 479 |
| Сколько в числе всего десятков? Чтобы определить количество десятков, записываем всё число без разряда единиц (то есть разряда до десятков). | 203 847 _ |
| Сколько в числе всего сотен? Чтобы определить количество сотен, записываем всё число без разрядов десятков и единиц (то есть разрядов до сотен). | 203 84 _ _ |
| Сколько в числе всего единиц тысяч? Чтобы определить количество единиц тысяч, записываем всё число без разрядов сотен, десятков и единиц (то есть разрядов до единиц тысяч). | 2 038 _ _ _ |
| Сколько в числе всего десятков тысяч? Чтобы определить количество десятков тысяч, записываем всё число без разрядов единиц тысяч, сотен, десятков и единиц (то есть разрядов до десятков тысяч). | 2 03 _ _ _ _ |
| Сколько в числе всего сотен тысяч? Чтобы определить количество сотен тысяч, записываем всё число без разрядов десятков тысяч, единиц тысяч, сотен, десятков и единиц (то есть разрядов до сотен тысяч). | 2 0 _ _ _ _ _ |
| Сколько в числе всего единиц миллионов? Чтобы определить количество единиц миллионов, записываем всё число без разрядов сотен тысяч, десятков тысяч, единиц тысяч, сотен, десятков и единиц (то есть разрядов до единиц миллионов) | 2 _ _ _ _ _ _ |
- В этом числе содержится:
- 2 единицы класса миллионов (третьего класса)
- 38 единицы класса тысяч (второго класса)
- 479 единицы класса единиц (первого класса)
Советуем обратить особое внимание на данную тему, так как умение раскладывать числа на разрядные слагаемые поможет вам при устном счёте и решении примеров с многозначными числами.
Для проверки своих результатов вы также можете воспользоваться нашим калькулятором разложения числа на разрядные слагаемые онлайн.
Источник
Число по разрядам онлайн
Калькулятор раскладывает натуральное число на разрядные слагаемые. Возможно раскладывать числа до 18 знаков.
Как разложить натуральное число по разрядам
Разрядные слагаемые записываются от большего к меньшему. Нули не учитываются. Двигаясь слева направо берём поочерёдно по одной цифре. Оставшиеся цифры заменяем на нули. Сумма разрядных слагаемых числа равна этому числу.
Разберём пример. Разложим число 41200 на разряды. Двигаясь слева направо по числу.
Берём первую цифру 4 после неё идёт ещё 4 цифры. Меняем их на нули и записываем 40000(четыре десятка тысяч).
Берём вторую цифру 1 после неё идёт ещё 3 цифры. Меняем их на нули и записываем 3000(три единицы тысяч).
Берём третью цифру 2 после неё идёт ещё 2 цифры. Меняем их на нули и записываем 200(две сотни).
Дальше идут нули их мы не учитываем.
41200 = 40000 + 1000 + 200
Что такое разрядное слагаемое ?
Разрядное слагаемое это натуральное число, которое начинается с цифры отличной от нуля. Остальные цифры нули.
К примеру цифры 10, 20, 300, 500, 2000 и.т.д. являются разрядными слагаемыми
Разложить число на разрядные слагаемые можно несколькими способами.
Основной — 31255 =30000 + 1000 + 200 + 50 + 5
Текстовый — 31255 = (3)три десятка тысяч, (1)одна тысяча, (2)две сотни, (5)пять десятков, (5)пять единиц
Подробный — 31255 = 3×10000 + 1×1000 + 2×100 + 5×10 +5×1
Классы чисел
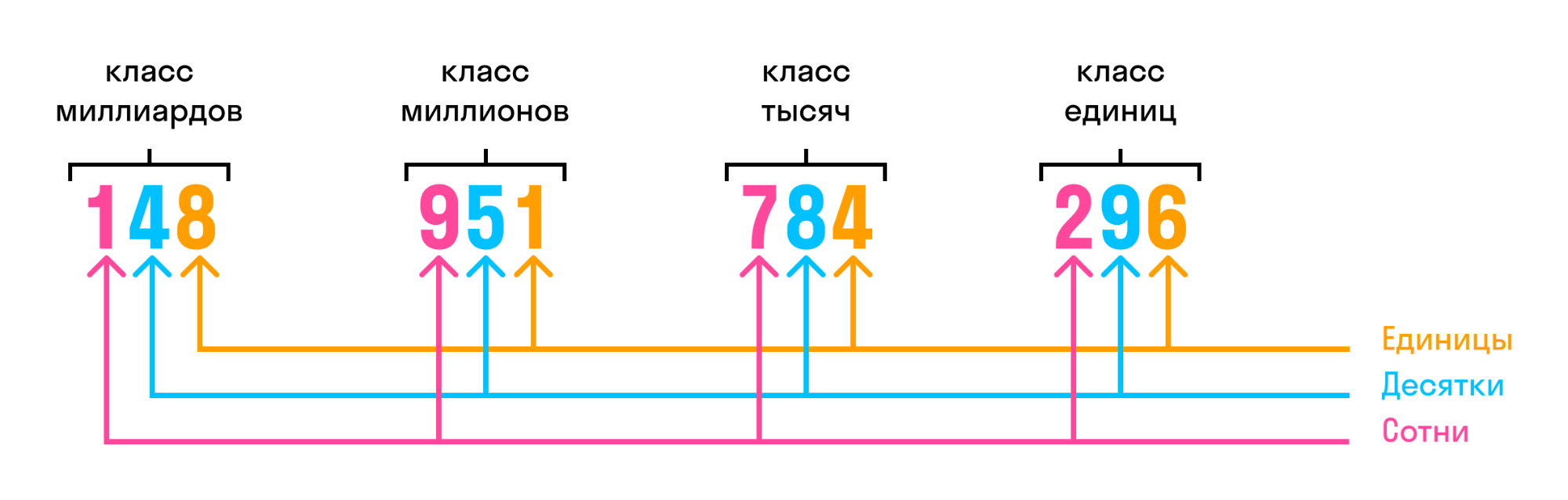
Многозначные числа разбивают на группы, справа налево по 3 цифры. Эти группы называются классами числа . В каждой из этих групп цифры справа налево обозначают единицы, десятки и сотни этого класса. Для удобства чтения числа многозначные числа разделяют пробелами между классами
123 456 789 — в данном числе 3 класса, 789 — класс единиц, 456 — класс тысяч, 123 — класс миллионов
Разряды чисел
Каждая цифра в записи многозначного числа занимает определённую позицию — разряд. Счёт разрядов начинается справа налево. Каждые три подрядидущие справа налево разряда составляют класс.
Источник
Сумма разрядных слагаемых
О чем эта статья:
Сумма разрядных слагаемых
Любое натуральное многозначное число можно представить в виде суммы разрядных слагаемых. Сумму разрядных слагаемых можно записать следующим образом:
- Число 35 состоит из 3 десятков и 5 единиц
35 = 3 десятка + 5 единиц = 3*10 = 30 + 5 = 35.
30 — разрядное слагаемое; 5 — разрядное слагаемое.
- Число 86 состоит из 8 десятков и 6 единиц
86 = 8 десятков + 6 единиц = 8*10 = 80 + 6 = 86
80 — разрядное слагаемое; 5 — разрядное слагаемое.
- Число 356 состоит из 3 сотен, 5 десятков и 6 единиц
356 = 3 сотни + 5 десятков + 6 единиц = 3*100 + 5*10 + 6 = 300+50+6 = 356.
300, 50, 6 — разрядные слагаемые.
Разряды и классы чисел
Чтобы без труда записывать числа в виде суммы разрядных слагаемых, нужно безошибочно определять класс и разряд числа.
В многозначном числе цифры справа налево разбиваются на группы по три цифры. Такие группы называют классами.
Названия классов многозначных чисел:
- первый — класс единиц,
- второй — класс тысяч,
- третий — класс миллионов,
- четвёртый — класс миллиардов,
- пятый — класс триллионов,
- шестой — класс квадриллионов,
- седьмой — класс квинтиллионов,
- восьмой — класс секстиллионов.
Чтобы чтение многозначного числа не превращалось в головоломку, при записи лучше разграничивать число по классам. Вот так:
- 345 466 129 350 вместо 345466129350
Читаться такое число будет слева направо: триста сорок пять миллиардов четыреста шестьдесят шесть миллионов сто двадцать девять тысяч триста пятьдесят.
Разряд — это место, которое занимает цифра в записи многозначного числа.
Разряды считаются справа налево. Первая цифра справа в записи числа относится к первому разряду.
- Например, в числе 128 656 374 252 разряды считаются справа налево: 2 — первый разряд; 5 — второй разряд; 2 — третий разряд; 4 — четвертый разряд; 7 — пятый разряд; 3 — шестой разряд; 6 — седьмой разряд; 5 — восьмой разряд; 6 — девятый разряд; 8 — десятый разряд; 2 — одиннадцатый разряд; 1 — двенадцатый разряд.
Разрядные единицы — это единицы, десятки, сотни, тысячи, миллионы.
Все разрядные единицы, за исключением простых единиц, — составные единицы. Каждые десять единиц одного разряда составляют одну единицу следующего разряда.
- 10 единиц = 1 десяток;
- 10 десятков = 1 сотня;
- 10 сотен = 1 тысяча;
- 10 тысяч = 1 десяток тысяч;
- 10 десятков тысяч = 1 сотня тысяч;
- 10 сотен тысяч = 1 миллион.
Если составная единица больше другой единицы — она называется единицей высшего разряда. Если меньше, то единицей низшего разряда. Так, например, сотня — единица высшего разряда относительно десятка, но низшего разряда относительно тысячи.
Чтобы выяснить сколько всего в числе единиц определенного разряда, нужно мысленно вычеркнуть из числа все цифры низшего разряда.
- Например, нужно сказать, сколько сотен в числе 5689.
Это значит, нужно выяснить, сколько сотен заключается в тысячах и в сотнях этого числа. 5689 — на третьем месте в классе единиц стоит цифра 6, значит в числе есть 6 сотен. Следующая влево цифра — 5 (тысячи). 1 тысяча = 10 сотен. 5 тысяч = 50 сотен. Всего в числе 56 сотен.
Если в разряде стоит цифра 0, то это означает отсутствие единиц, десятков, сотен и т.д., в зависимости от того, где именно содержится цифра.
Иногда бывает необходимо не только разложить число на разрядные слагаемые, но и определить количество единиц какого-то определенного разряда.
В такой ситуации можете выполнить подробный разбор числа.
- Разберем число 6 057 386
Шесть миллионов пятьдесят семь тысяч триста восемьдесят шесть
6 057 386 = 6 * 1 000 000 + 0 * 100 000 + 5 * 10 000 + 7 * 1000 + 3 * 100 + 8 * 10 + 6 = 6 000 000 + 50 000 + 7 000 + 300 + 80 + 6.
Из чего состоит это число? Из:
- шести единиц миллионов (6 * 1 000 000);
- пяти десятков тысяч (5 * 10 000);
- семи единиц тысяч (7 * 1000);
- трех сотен (3 * 100);
- восьми десятков (8 * 10);
- шести единиц (6).
Для того, чтобы алгоритм разложения числа на простые слагаемые был всегда под рукой, сохраняйте себе табличку с примером. В ней вы найдете вопросы, которые помогут разложите любое число.
Определите, сколько единиц в числе 5 068 252.
1. Определяем сколько всего единиц в числе.
2. Определяем количество десятков.
Записываем число без первого разряда (единицы).
3. Определяем количество сотен.
Записываем число без первого
и второго разрядов (десятки и сотни).
4. Определяем количество единиц тысяч.
Записываем число без первого, второго,
третьего разрядов (единицы, десятки, сотни).
5. Определяем количество десятков тысяч.
Записываем число без первого, второго, третьего,
четвертого разрядов (единицы, десятки, сотни, единицы тысяч).
6. Определяем количество сотен тысяч.
Записываем число без десятков тысяч, единиц тысяч,
сотен и единиц.
7. Определяем количество единиц миллионов.
Записываем число без сотен тысяч, десятков тысяч,
единиц тысяч, сотен, десятков, единиц.
Расписав таким образом число, мы выяснили, что в числе 5 068 252: 5 единиц класса миллионов (3 класс); 68 единиц класса тысяч (2 класс); 252 единицы класса единиц (1 класс).
Может показаться, что такой подробный разбор ни к чему, что и без того все понятно, но многоразрядные многозначные числа — коварны. Лучше хорошенько потренироваться, используя все вспомогательные материалы, как эта табличка, а потом уже раскладывать любое число за секунды и в уме.
Примеры
Внимательно просмотрите примеры и попробуйте самостоятельно представить числа в виде суммы разрядных слагаемых.
Представьте в виде суммы разрядных слагаемых:
- 84 610
84 610 = 8 * 10 000 + 4 * 1 000 + 6 * 100 + 10
84 610 = 80 000 + 4 000 + 600 + 10. - 45 317
45 317 = 4 * 10 000 + 5 * 1000 + 3 * 100 + 17
45 317 = 40 000 + 5 000 + 300 + 17. - 56 789
56 789 = 5 * 10 000 + 6 * 1000 + 7 * 100 + 8 * 10 + 9
56 789 = 50 000 + 6 000 + 700 + 80 + 9. - 345 677
345 677 = 3 * 100 000 + 4 * 10 000 + 5 * 1000 + 6 * 100 + 7 * 10 + 7
345 677 = 300 000 + 40 000 + 5 000 + 600 + 70 + 7. - 687 543
687 543 = 6 * 100 000 + 8 * 10 000 + 7 * 1000 + 5 * 100 + 4 * 10 + 3
687 543 = 600 000 + 80 000 + 7 000 + 500 + 40 + 3. - 877 589
877 589 = 8 * 100 000 + 7 * 10 000 + 7 * 1000 + 5 * 10 + 8 * 10 + 9
877 589 = 800 000 + 70 000 + 7 000 + 500 + 80 + 9.
Как видите, все довольно просто. Занятие весьма успокаивающее, медитативное. Приятно сесть после тяжелого дня и пораскладывать числа на разрядные слагаемые.
Если вдруг так вышло, что вы не расслабляетесь при виде цифр, то воспользуйтесь онлайн-калькулятором. В интернете таких калькуляторов немало, вот один из них.
- 4 895 634
4 895 634 = 4 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 5 * 1000 + 6 * 100 + 3 * 10 + 4
4 895 634 = 4 000 000 + 800 000 + 90 000 + 5 000 + 600 + 30 +4. - 8 675 349
8 675 349 = 8 * 1 000 000 + 6 * 100 000 + 7 * 10 000 + 5 * 1000 + 3 * 100 + 4 * 10 + 9
8 675 349 = 8 000 000 + 600 000 + 70 000 + 5 000 + 300 + 40 + 9. - 77 897 125
77 897 125 = 7 * 10 000 000 + 7 * 1 000 000 + 8 * 100 000 + 9 * 10 000 + 7 * 1000 + 1 * 100 + 2 * 10 + 5
77 897 125 = 70 000 000 + 7 000 000 + 800 000 + 90 000 + 7 000 + 100 + 20 + 5. - 656 734 212
656 734 212 = 6 * 100 000 000 + 5 * 10 000 000 + 6 * 1 000 000 + 7 * 100 000 + 3 * 10 000 + 4 * 1000 + 2 * 100 + 1 * 10 + 2
656 734 212 = 600 000 000 + 50 000 000 + 6 000 000 + 700 000 + 30 000 + 4 000 + 200 + 10 + 2.
Так вы сможете разложить на разрядные слагаемые любое, даже самое гигантское, число. Важно разобраться в разрядах и классах чисел, тогда вы точно ничего не перепутаете.
Источник
Урок 11 Бесплатно Разложение числа по разрядам. Способы сложение натуральных чисел
Вы уже имеете общее представление об арифметической операции сложения и знаете свойства сложения натуральных чисел.
Сегодня вспомним наименования разрядов и классов.
Выясним, как записывают и читают большие натуральные числа.
Разберемся, что представляют собой разрядные слагаемые и как определить сумму разрядных слагаемых.
Познакомимся с различными способами и приемами сложения многозначных натуральных чисел, закрепим полученные знания на примерах.
Разряды и классы
С давних времен люди стремились не только уметь считать, но и уметь записывать числа.
Сначала для записи чисел применяли черточки, точки, метки и другие способы представления количества чего-либо, сейчас для этих целей используют цифры.
Сегодня цифры и числа окружают нас повсюду.
Мы не можем себе представить дату без чисел, невозможно измерить рост, массу, время, возраст, считать предметы, совершить покупку, продать, позвонить и т.д.
Число- это математическое понятие, которое используется для количественной характеристики, нумерации объектов и их частей, сравнения.
Каждое число состоит из цифр.
Цифрой называют знак, используемый для записи числа.
Цифры, которые мы используем в повседневной жизни, называют арабскими.
Их существует всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Все цифры кроме нуля называют значащими.
Нуль- это знак, который не указывает никакого числа, т.е. указывает на его отсутствие.
Запись числа с помощью десяти арабских цифр называют десятичной системой счисления.
Название системы счисления определяется ее основанием: количеством цифр, которые используются в данной системе счисления.
Цифры, из которых строятся числа десятичной системы счисления, называют узловыми:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Все остальные числа, которые состоят из узловых, называют алгоритмическими, например, 48, 35, 675, 2468 и т.д.
Десятичная система счисления является позиционной системой счисления, так как значение каждой цифры, из которых состоит число, зависит от ее позиции (места) в этом числе.
Место записи цифры в числе называют разрядом числа.
Счет разрядов идет справа налево.
В записи числа первая цифра справа называется цифрой первого разряда (разряд единиц)- это самый младший разряд.
Идущая следом за разрядом единиц, вторая цифра в числе — это цифра второго разряда, обозначающая количество десятков в числе (разряд десятков).
Третья цифра с конца числа указывает на количество сотен в числе — цифра третьего разряда (разряд сотен).
Например, в числе 182 три разряда: первый разряд (разряд единиц) состоит из 2 единиц, второй разряд (разряд десятков) состоит из 8 десятков, третий разряд (разряд сотен) состоит из 1 сотни.
Если в записи числа вместо какого-либо разряда стоит «0» (нуль), то это означает, что цифра данного разряда отсутствует.
Сравним прочтение чисел 201 и 241
Каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Например, единицы называют простыми единицами.
10 простых единиц составляют десяток.
10 десятков составляют сотню.
10 сотен составляют тысячу.
10 тысяч (один десяток тысяч) составляют десять тысяч (10000)
10 десятков тысяч составляют сто тысяч (100000)
Числа, которые записаны с помощью одной цифры, называют однозначными числами (числами первого порядка).
Числа, записанные с помощью двух цифр, называют двузначными числами (числами второго порядка).
Числа, которые состоят из трех цифр, называют трехзначными (числами третьего порядка) и т.д.
Пример:
1, 2, 5, 6— однозначные числа.
Самое маленькое однозначное натуральное число 1, самое большое- 9
10, 24, 38, 85— двузначные числа.
Самое маленькое двузначное натуральное число 10, самое большое- 99
278, 456, 882, 312— трехзначные числа.
Самое маленькое трехзначное натуральное число 100, самое большое- 999
Числа, для записи которых используют более одной цифры, называют многозначными числами.
Для удобства чтения многозначных чисел их разбивают на группы по три цифры, начиная справа; такие группы цифр называют классами.
Каждый класс содержит три разряда, записанных справа налево, начиная с разряда единиц, далее разряд десятков, затем идет разряд сотен.
Самый последний левый класс натурального многозначного числа может состоять из одного или двух разрядов.
Каждый класс имеет свое название.
Три первые цифры с конца числа составляют класс единиц, три следующие — класс тысяч, далее идет класс миллионов, затем класс миллиардов и т.д.
Разряды повторяются по очереди в каждом классе, обозначая единицы, десятки и сотни соответствующих классов тысяч, миллионов, миллиардов и т.д.
Изобразим таблицу классов и разрядов натуральных чисел.
Таблица классов и разрядов чисел
У меня есть дополнительная информация к этой части урока!

Числа, которые имеют более 12 разрядов, т.е. числа от пятого класса и выше относятся к большим числам.
Числа, идущие после миллиарда названы в соответствии с латинскими наименованиями числительных.
Каждый последующий класс больших чисел содержит 1000 предыдущих.
1000 миллиардов = 1 триллион (представляет собой единицу и 12 нулей).
«Три» по латыни означает число «три».
1000 триллионов = 1 квадриллион (представляет собой единицу и 15 нулей)
«Квадра» по латыни означает число «четыре».
1000 квадриллионов = 1 квинтиллион (представляет собой единицу и 18 нулей)
«Квинта» по латыни- «пять» и т.д.
«Числа-гиганты» в повседневной жизни используют редко.
Применяются в основном в физике и астрономии для измерения массы и размеров звезд и планет, для расчета расстояний до различных небесных тел, расстояний между ними и т.д.
Удивительно, но большие числа можно отметить в человеческом теле.
Так, например, человеческий мозг состоит из 100 миллиардов нервных клеток- нейронов.
Оказывается, в теле человека около 100 миллиардов мелких кровеносных сосудов — капилляров.
Посмотрим, как правильно читается большое число.
Чтобы прочитать многозначное натуральное число 184567483265, разобьем его на классы: Получим число вида: 184 567 483 265.
Прочитаем число, называя по очереди число единиц каждого класса слева направо.
При чтении класса единиц название данного класса, которым заканчивается любое натуральное число, не произносится.
184 миллиарда 567 миллионов 483 тысячи 265.
Не произносится также название класса, все три цифры которого нули.
Например, число 149500000 километров (число равное расстоянию от Земли до Солнца) прочитаем так: 149 миллионов 500 тысяч километров.
Пройти тест и получить оценку можно после входа или регистрации
Способы сложения натуральных чисел
Вы уже имеете общее представление об операции сложения чисел и знаете свойства сложения натуральных чисел.
Уроком ранее мы выяснили, что сложение- это арифметическая операция объединения исчисляемых объектов в одно целое.
Результат сложения чисел называют суммой этих чисел.
Складываемые числа называют слагаемыми.
Для записи сложения используют знак плюс «+»
В повседневной жизни, на работе, на учебе возникает необходимость оперативно и качественно решать задачи и производить определенные арифметические действия, выбирая для этого оптимально удобный способ решения.
Сейчас рассмотрим некоторые способы и приемы, позволяющие верно, быстро и легко вычислит сумму натуральных чисел.
1. Таблица сложения натуральных чисел
Для сложения чисел первого десятка удобно пользоваться таблицей сложения, с которой вы знакомились в начальных классах.
Запомнив данную таблицу наизусть, легко и просто выполнить задание на вычисление суммы чисел.
Разберем правила пользования таблицей сложения натуральных чисел.
Известно, что операция сложения выглядит так:
Слагаемое №1 + Слагаемое №2 = Сумма
Таблица представляет собой квадрат, разбитый на десять строк и десять столбцов.
По верхнему краю и по левому краю пронумерованы ячейки от 1 до 10
У меня есть дополнительная информация к этой части урока!

Алгоритм сложения двух натуральных чисел с помощью таблицы:
1. В самой верхней строке необходимо выбрать из десяти ячеек ту, в которой содержится значение первого слагаемого.
2. Выбрать в самом левом столбце ячейку, в которой находится значение второго слагаемого.
3. Суммой будет являться число, расположенное в ячейке, образованной пересечением соответствующих столбца и строки в поле таблицы.
Например, чтобы сложить два натуральных числа 4 и 7, нужно выполнить следующие действия:
- В верхней первой строке таблицы найти ячейку со значением 4.
- В левом крайнем столбце найти ячейку со значением 7.
- На пересечении соответствующих столбца и строки находится ячейка с числом 11 — это число является суммой чисел 4 и 7.
Таким образом, 4 + 7 = 11
Такой же результат будет получен, если с помощью таблицы сложим 7 и 4.
- Необходимо в первой строке таблиц найти число 7.
- В левом крайнем столбце найти ячейку со значением 4.
- На пересечении соответствующих столбца и строки также находится ячейка с числом 11 — это число является суммой чисел 7 и 4.
Таким образом, 7 + 4 = 11
Таблицей удобно пользоваться при сложении многозначных чисел по разрядам, если условно принять, что в таблице складываются десятки с десятками или сотни с сотнями, или тысячи с тысячами и т.д.
Пример:
Найдите сумму чисел 20 и 60 с помощью таблицы сложения натуральных чисел.
С помощью таблицы уже известным способом сложим числа 2 и 6, суммой данных чисел является ячейка со значением 8.
Условно представим, что ячейка со значением 2— это 2 десятка, ячейка со значением 6— это 6 десятков.
Следовательно, ячейка с результатом 8, образованная пересечением соответствующего столбца и строки, по смыслу означает 8 десятков.
20 + 60 = 80
Ответ: 80
Для перехода при сложении на следующий разряд вспомним, что каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Пример:
Вычислите по таблице сумму чисел 700 и 300.
С помощью таблицы уже известным способом сложим числа 7 и 3, суммой данных чисел является ячейка со значением 10
Условно представим, что ячейка со значением 7— это 7 сотен, ячейка со значением 3 означает 3 сотни.
Следовательно, ячейка с результатом 10, образованная пересечением соответствующего столбца и строки, по смыслу означает 10 сотен.
Нам известно, что 10 сотен = 1000
Таким образом, получаем 700 + 300 = 1000
Ответ: 1000
Пример:
Вычислите сумму 60 и 70 с помощью таблицы сложения.
По таблице сложения чисел видно, что 6 + 7 = 13
Следовательно, если сложить 6 десятков и 7 десятков, получим 13 десятков.
Так как число 13 состоит из 1 десятка и 3 единиц, то 13 десятков состоят из 10 десятков и 3 десятков.
10 десятков = 100
3 десятка = 30
Получим 100 + 30 = 130.
Ответ: 130
Конечно, таблица сложения натуральных чисел позволяет наглядно легко и быстро определить сумму чисел, но не всегда она находится под рукой.
2. Способ поразрядного сложения натуральных чисел.
Рассмотрим еще один способ определения суммы чисел.
Первым делом научимся представлять натуральные числа в виде суммы разрядных слагаемых.
Разрядные слагаемые натурального числа имеют ряд характерных признаков:
1. Разрядные слагаемые- это числа, в записи которых находится только одна цифра, отличная от нуля.
Например, 10, 200, 6000, 40000 и т.д.
2. Разрядные слагаемые одного натурального числа имеют разное количество знаков в своей записи (т.е. состоят из разного количества цифр).
3. Количество разрядных слагаемых натурального числа должно быть равно количеству цифр, отличных от нуля, в записи числа.
Сумма разрядных слагаемых— это запись многозначного числа, как суммы его разрядных единиц.
Сумма разрядных слагаемых равна исходному натуральному числу.
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Для этого необходимо:
1. Определить по количеству цифр в числе количество разрядных слагаемых, отличных от нуля.
2. Определить количество единиц, десятков, сотен, тысяч и т.д.
3. Записать число в виде суммы разрядных слагаемых.
Пример:
Разложите натуральное число 2456 в виде суммы разрядных слагаемых.
Число 2456 представляет собой сумму четырех разрядных слагаемых (так как число состоит из 4 цифр, неравных нулю).
Число 2456 содержит:
2456 = 2 тысячи + 4 сотни + 5 десятков + 6 единиц = 2000 + 400 + 50 + 6
Рассмотрим алгоритм поразрядного сложения натуральных чисел.
1. Слагаемые разложить на разрядные слагаемые.
2. Выполнить сложение одноименных разрядов (единиц с единицами, десятки с десятками и т.д.) используя при этом переместительное и сочетательное свойства сложения.
Пример:
Найдите сумму чисел 245 и 25 способом последовательного поразрядного сложения.
Разложим первое и второе слагаемое на разрядные слагаемые.
245 = 2 сотни + 4 десятка + 5 единиц = 200 + 40 + 5
25 = 2 десятка + 5 единиц = 20 + 5
Выполним сложение одноименных разрядов чисел 245 и 25.
245 + 25 = 200 + 40 + 5 + 20 + 5 = 200 + (40 + 20) + (5 + 5) = 200 + (60 + 10) = 200 + 70 = 270
Получаем 245 + 25 = 270
Ответ: 270
3. Сложение натуральных чисел «столбиком»
Рассмотренный способ поразрядного сложения довольно громоздкий в оформлении и не очень удобный для определения суммы больших чисел или нескольких больших чисел.
Поэтому часто многозначные числа складывают в столбик.
Чтобы сложить натуральные числа данным способом, нужно записать слагаемые в столбик так, чтобы цифры одноименных разрядов находились друг под другом (единицы под единицами, десятки под десятками, сотни под сотнями и т.д.).
При сложении столбиком самая правая цифра одного числа (разряд единиц первого слагаемого) должна располагаться под самой правой цифрой другого числа (разряд единиц второго слагаемого).
Нам известно, что от перестановки слагаемых сумма не меняется, следовательно, записывать слагаемые в столбик можно в любом порядке.
Затем слева между числами-слагаемыми ставится знак плюс «+».
Под нижним слагаемым проводится горизонтальная черта.
Сложение чисел начинается с разряда единиц (с крайнего правого столбца).
Складывают цифры одного разряда, результат записывают под горизонтальной чертой под тем разрядом, в котором выполнялось сложение.
Если в результате получается число меньше 10 (однозначное число), то оно записывается в столбик соответствующего разряда под чертой.
Если в результате получается двузначное число, то под чертой записывается значение разряда единиц полученного числа, а число десятков либо запоминается (держится в уме), либо подписывается сверху над следующим столбиком в дополнительной строке.
Далее складываются числа в следующем столбике, т.е. складываются значение следующего разряда слагаемых.
Действия совершаются аналогично изложенным выше, однако к суме еще добавляется число десятков, которые «держали в уме» (если такое было).
Соответственно, если получается однозначное число, его записывают под чертой в столбик соответствующего разряда.
Если число в результате сложения получается двузначное, то снова под линией записывается число единиц полученного промежуточного значения, а значение десятков запоминается или записывается в дополнительной строке.
Так происходит переход к следующему столбику (следующим разрядам слагаемых) и производятся все выше описанные действия.
Натуральное число, которое образуется после завершения операции сложения, является результатом суммы исходных чисел.
Пример:
Выполните сложение двух чисел 75806 и 2798.
Запишем два числа в столбик так, чтобы одноименные разряды стояли друг под другом.
Между числами поставим знак плюс «+», под нижним слагаемым проведем горизонтальную черту.
Складываем числа из правого столбца: 6 и 8.
Получаем число 14— двузначное число.
Под горизонтальной линией записываем число 4 (значение разряда единиц числа 14), а число 1 (значение разряда десятков числа 14) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Продолжаем вычисление, складываем цифры слагаемых, стоящих во втором столбце справа.
Так как 0 + 0 = 0, но была запомнена 1, то получим 0 + 0 + 1 = 1
Число 1— однозначное число, следовательно, его просто записываем под чертой в соответствующем разряде.
Переходим к следующему столбцу.
Складываем 8 и 9, при этом в памяти нет никаких запомненных чисел, поэтому больше ничего к ним не прибавляем
8 + 9 = 17
Получили двузначное число 17.
Следовательно, число 7 записываем под горизонтальной чертой (значение разряда единиц числа 17), а число 1 (значение разряда десятков числа 17) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Переходим к четвертому столбцу.
Складываем 5 и 7.
В памяти была запомнена 1, поэтому к сумме чисел 5 и 7 прибавляем 1.
5 + 7 + 1 = 13
Получили двузначное число 13.
Следовательно, число 3 записываем под горизонтальной чертой, а число 1 запоминаем, переносим в следующий разряд.
На последнем шаге складываем 2 и 7
2 + 7 = 9
К 9 прибавляем запомненную 1, получаем: 9 + 1 = 10
Так как 10 — двузначное число, число 0 записываем под горизонтальной чертой, а число 1 запоминаем.
Но в следующем столбце исходные слагаемые не имеют цифр, запомненную 1 сносим вниз и записываем под чертой.
Сложение двух натуральных чисел 75806 и 27908 завершено, сумма данных чисел равна 103714
75806 + 27908 = 103714
Ответ: 103714
Столбиком можно складывать различное количество слагаемых.
Алгоритм выполнения операции сложения в столбик нескольких слагаемых будет абсолютно аналогичным.
4. Группировка слагаемых и округление натуральных чисел.
Данный способ сложения натуральных чисел кратко уже был рассмотрен на прошлом уроке.
Известно, что число, которое оканчивается на нуль или несколько нулей, называют круглым числом.
С круглыми числами легко совершать арифметические операции.
Сложение способом округления натуральных чисел применяют, когда из слагаемых можно выбрать такие, которые в сумме будут давать круглые числа.
Разность между круглым и исходным числом называется арифметическим дополнением.
Чтобы произвести сложение многозначных натуральных чисел способом округления, необходимо:
1. Одно из слагаемых, которое близко к круглому числу, округлить.
2. Выполнить операцию сложения.
3. Из полученной суммы вычесть арифметическое дополнение.
Пример:
Найдите сумму чисел 1448 и 298
Округлим число 298 до 300, а затем вычтем из полученной суммы арифметическое дополнение, равное 2
Получим выражение вида:
1448 + 298 = (1448 + 300) — 2 = 1748 — 2 = 1746
Ответ: 1746
Совместно с данным способом сложения натуральных чисел используют группировку слагаемых и применяют основные свойства сложения.
При вычислении суммы, состоящей из трех и более слагаемых, удобно использовать переместительное и сочетательное свойство сложения, группируя слагаемые, объединяя их по определенному признаку с помощью скобок таким образом, чтобы в сумме они давали круглые числа.
Пример:
Найдите сумму чисел 46 + 28 + 134 + 61
Группируем числа так, чтобы в результате сложения этих чисел получалось круглое число.
Используя переместительное и сочетательное свойство сложения, переставим местами слагаемые и сгруппируем их.
46 + 28 + 134 + 61 = (46 + 134) + (28 + 61) = 180 + 89
Округлим число 89 до 90
В связи с этим из суммы чисел 180 и 90 вычтем арифметическое дополнение, равное 1
180 + 89 = (180 + 90) — 1 = 270 — 1 = 269
Ответ: 269
Пройти тест и получить оценку можно после входа или регистрации
Источник