- Способ плоскостей посредников алгоритм
- Метод плоскостей | AutoCAD
- Метод секущих плоскостей, немного теории
- Условия задачи
- Решение
- Строим секущие плоскости, вид с боку
- Секущие плоскости, вид сверху
- Точки пересечения секущих плоскостей
- Линия пересечения
- Проверка вида линии пересечения
- Резюме
- Способ плоскостей посредников алгоритм
- Способ плоскостей посредников алгоритм
Способ плоскостей посредников алгоритм
Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)
При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.
Существуют следующие случаи взаимного пересечения поверхностей:
1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;
2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;
3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;
4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).
Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.
Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.
Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.
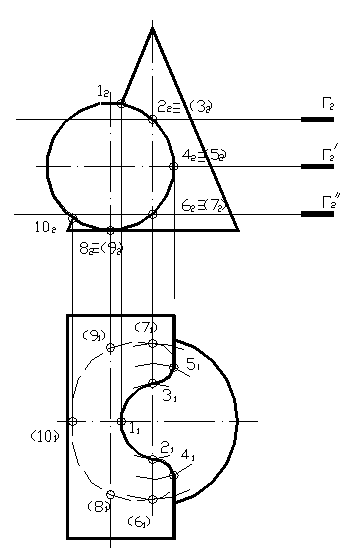
Рисунок 53
1. Какие бывают случаи взаимного пересечения поверхностей?
2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?
3. Какие точки называются опорными?
4. Как определять видимость линии пересечения и поверхностей?
5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Метод плоскостей | AutoCAD
В этом уроке рассмотрим одну из самых распространенных задач начертательной геометрии – построение пересечения поверхностей методом секущих плоскостей и способ ее решения средствами AutoСАD.
Метод секущих плоскостей, немного теории
Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры.
Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей.
Условия задачи
Зададим условия: пусть необходимо построить пересечение полусферы и конуса, расположенных таким образом:
Размеры показаны для наглядности, проставлять их на чертеже не нужно.
Решение
Строим секущие плоскости, вид с боку
Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):
Секущие плоскости, вид сверху
Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху. Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:
Точки пересечения секущих плоскостей
Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:
Видно, что в районе верхней точки построение недостаточно «информативно», т.е. будет полезным построить еще одну секущую плоскость:
Вот еще две точки, заданные этой плоскостью:
Линия пересечения
Соединив на виде сверху полученные точки сплайном (команда Сплайн), мы получим приближенную линию пересечения двух поверхностей:
Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде. Линии построения выделены желтым цветом:
Поскольку исходные поверхности (и, соответственно, линия их пересечения) симметричны относительно плоскости, параллельной фронтальной плоскости проекции, достаточно перенести только половину точек. В нашем частном случае невидимая на фронтальном виде часть кривой «спрятана» за видимой, а верхняя точка является точкой разделения видимой и невидимой частей.
Проверка вида линии пересечения
Полезно проверить правильность наших построений средствами 3D-моделирования. Построим соответствующие фигуры, перейдя предварительно к интерфейсу 3D- моделирование , и сравним полученную модель с построением (для этого удобнее объединить объекты командой Объединить).
Резюме
Как видим, наше построение довольно точно передает реальную линию пересечения поверхностей вращения. И хотя современные средства моделирования позволяют строить такие пересечения гораздо быстрее, рассмотренные нами принципы очень полезны для понимания «механики» геометрических построений, без которого любой, даже самый современный инструмент 3D-моделирования превращается в сложную и непонятную игрушку.
Источник
Способ плоскостей посредников алгоритм
Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)
При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.
Существуют следующие случаи взаимного пересечения поверхностей:
1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;
2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;
3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;
4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).
Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.
Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.
Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.

Рисунок 53
1. Какие бывают случаи взаимного пересечения поверхностей?
2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?
3. Какие точки называются опорными?
4. Как определять видимость линии пересечения и поверхностей?
5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Способ плоскостей посредников алгоритм
Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)
При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.
Существуют следующие случаи взаимного пересечения поверхностей:
1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;
2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;
3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;
4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).
Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.
Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.
Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.
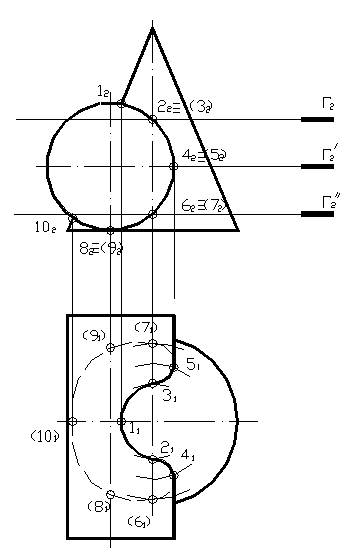
Рисунок 53
1. Какие бывают случаи взаимного пересечения поверхностей?
2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?
3. Какие точки называются опорными?
4. Как определять видимость линии пересечения и поверхностей?
5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник







