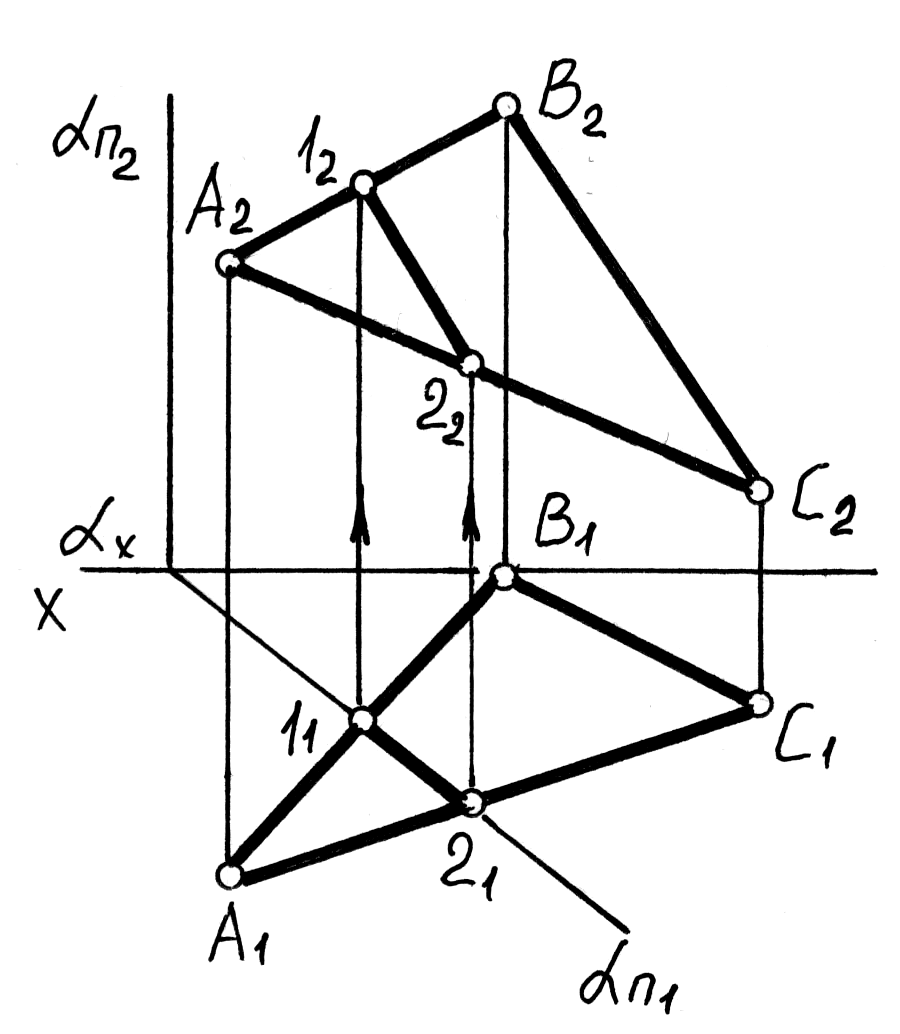
Способ плоскостей частного положения
Проекцией прямой, которая не перпендикулярна плоскости проекций, является прямая. Её положение определяется двумя точками, следовательно, для того чтобы построить проекцию прямой, достаточно построить проекции двух её точек.
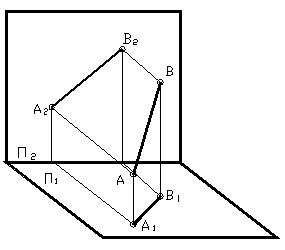
Рисунок 8
а) Прямой общего положения называется прямая, которая не параллельна и не перпендикулярна ни одной из плоскости проекций. Пример такой прямой изображён на рисунке 8. Комплексный чертёж этой прямой будет выглядеть следующим образом.
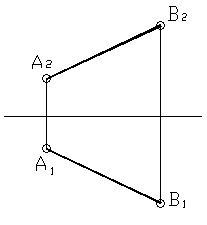
Рисунок 9
б) Прямые частного положения – это прямые, занимающие по отношению к плоскостям проекций особое положение, т.е. либо параллельные, либо перпендикулярные плоскостям проекций.
Первый подкласс прямых частного положения – прямые уровня. Это прямые, параллельные какой-либо плоскости проекций.
Горизонталь – прямая параллельная горизонтальной плоскости П1. Комплексный чертёж такой прямой изображён на рисунке 10.
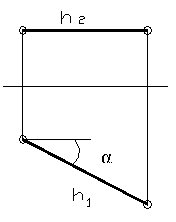
Рисунок 10
Фронтальная проекция горизонтали всегда параллельна прямой Х, а угол между осью Х и горизонтальной проекцией горизонтали составляет угол между прямой и фронтальной плоскостью проекций. Символическая запись: h // П1; α = Ð h П2.
Фронталь – прямая параллельная фронтальной плоскости П2. Комплексный чертёж фронтали изображён на рисунке 11.
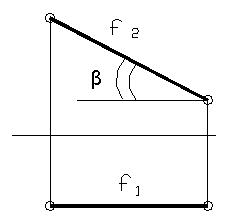
Рисунок 11
Горизонтальная проекция фронтали параллельна оси Х, а угол β — угол наклона фронтали к горизонтальной плоскости проекций; f2 // П2, β= Ð f1 П1.
Профильная прямая – это прямая, параллельная профильной плоскости П 3 . Комплексный чертёж профильной прямой изображён на рисунке 12. Горизонтальная и фронтальная проекции профильной прямой перпендикулярны оси Х, а углы α и β — соответственно, углы наклона прямой к плоскостям П 1 и П2.
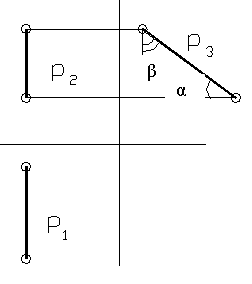
Рисунок 12.
Истинная величина прямых уровня или, так называемая натуральная величина, отображена на тех плоскостях, которым параллельны эти прямые.
Второй подкласс прямых частного положения – проецирующие прямые. Это прямые, перпендикулярные какой-либо плоскости проекций. К таким прямым относятся: горизонтально–проецирующая, фронтально-проецирующая и профильно-проецирующая прямые.
Их комплексные чертежи изображены соответственно на рисунке 13 (а, б, в).
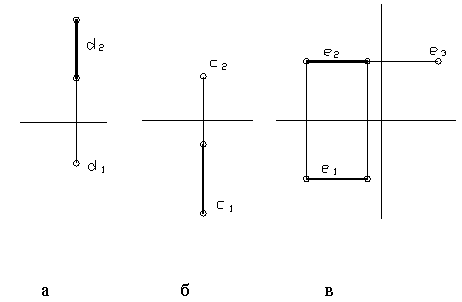
Рисунок 13
Натуральная величина горизонтально-проецирующей прямой – её фронтальная проекция, фронтально-проецирующей прямой – её горизонтальная проекция, а профильно-проецирующей прямой – её горизонтальная и фронтальная проекции.
а) три точки, не лежащие на одной прямой;
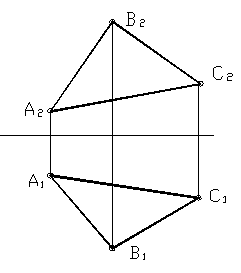
Рисунок 14
б) прямая и точка, не лежащая на ней;
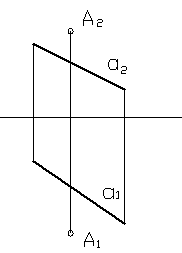
Рисунок 15
в) две параллельные прямые;
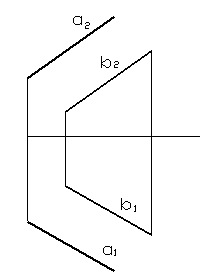
Рисунок 16
г) две пересекающиеся прямые;
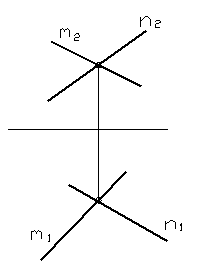
Рисунок 17
д) плоская фигура (многоугольник, круг и т.д.).
Плоскость общего положения не параллельна и не перпендикулярна ни одной из плоскостей проекций.
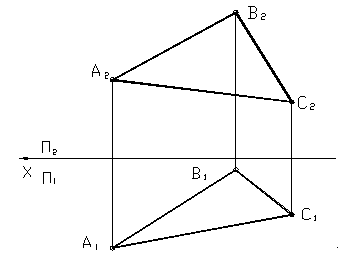
Рисунок 18
Плоскости частного положения аналогично прямой подразделяются на плоскости уровня и проецирующие плоскости. На рисунке 19 (а,б,в) изображены, соответственно, горизонтальная, фронтальная и профильная плоскости. Причём горизонтальная плоскость задана двумя параллельными прямыми, фронтальная и профильная плоскости – двумя пересекающимися прямыми.
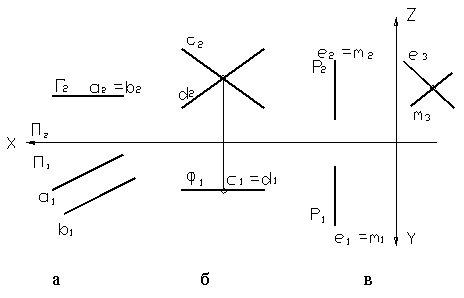
Рисунок 19
На рисунке 20 (а, б, в) показаны проецирующие плоскости. Горизонтально-проецирующая (рис. 20а) задана треугольником, фронтально-проецирующая (рис. 20б) — параллельными прямыми и профильно-проецирующая (рис. 20в) – пересекающимися прямыми.
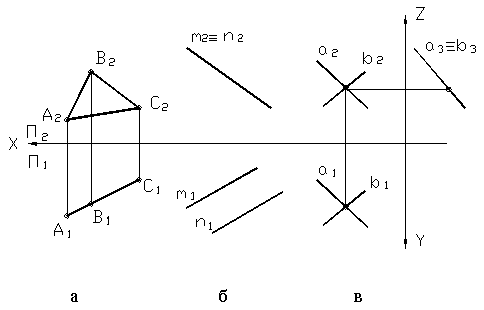
Рисунок 20
1. Как образуется комплексный чертеж прямой линии?
2. Прямые какого положения вы знаете?
3. Назовите прямые уровня.
4. Как называется прямая, проекцией которой на горизонтальной плоскости будет точка?
5. Перечислите способы задания плоскости.
6. Дайте определение плоскости общего положения.
7. Какие бывают плоскости частного положения? Как они называются и как выглядят на комплексном чертеже?
© ФГБОУ ВПО Красноярский государственный аграрный университет
Источник
Плоскости частного положения



Плоскости относительно плоскостей проекций могут быть общего и частного положения. Плоскости частного положения — это плоскости перпендикулярные или параллельные какой-либо плоскости проекций.
Плоскости перпендикулярные одной из плоскостей проекций, называются проецирующими.
1. Горизонтально проецирующая плоскость перпендикулярна горизонтальной плоскости проекций p1 (рис. 4.3а).
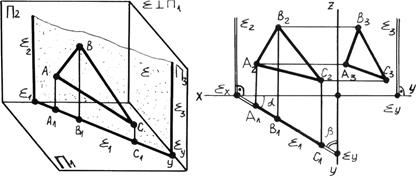
Рис. 4.3а. Горизонтально проецирующая плоскость.
Фронтальный след S1 перпендикулярен оси x. Профильный след S3 перпендикулярен оси y.
Ða — угол наклона плоскости S к плоскости p2. Ðb — угол наклона плоскости S к плоскости p3. Горизонтальная проекция всех точек плоскости S совпадает с её горизонтальными следами.
2. Фронтально проецирующая плоскость перпендикулярна фронтальной плоскости проекций p2 (рис. 4.3б) горизонтальный след l1 — перпендикулярен оси x, профильный след l3 перпендикулярен оси z, Ðj — угол наклона плоскости l к плоскости p1. Ðb — угол наклона плоскости l к плоскости p3. Фронтальные проекция всех точек плоскости l совпадают с ее фронтальным следом.
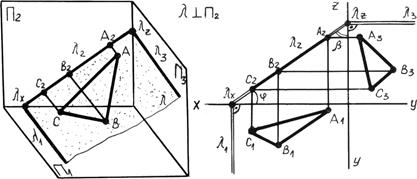
Рис. 4.3б. Фронтально проецирующая плоскость.
3. Профильно проецирующая плоскость перпендикулярна профильной плоскости проекций p3 (рис. 4.3.в).

Рис. 4.3в. Профильно проецирующая плоскость.
Горизонтальный след D1 перпендикулярен оси y, фронтальный след D2 перпендикулярен оси z.
Ðj — угол наклона плоскости D к плоскости p1.Ða — угол наклона плоскости D к плоскости p2. Профильные проекции всех точек плоскости D совпадают с ее профильным следом.
Плоскости параллельные какой-либо из плоскостей проекций и перпендикулярные двум другим называются плоскостями уровня.
1. Горизонтальные плоскость уровня параллельна плоскости p1 и перпендикулярна плоскостям p2 и p3 (рис. 4.4а).
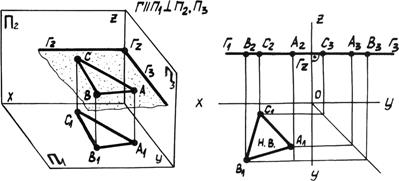
Рис. 4.4а. Горизонтальные плоскость уровня.
Фронтальная и профильная проекции плоскости совпадают с ее следами G1 и G2, которые перпендикулярны оси z. На горизонтальную плоскость p1 любая фигура, расположенная в плоскости G, проецируется без искажения на p1.
2. Фронтальная плоскость уровня параллельна плоскости p2 и перпендикулярна плоскостям p1 и p3 (рис. 4.4б).
Горизонтальная и профильная проекции плоскости совпадают с её следами q1 и q3, которые перпендикулярны оси y. На фронтальную плоскость p2 любая фигура, расположенная в плоскости q, проецируется без искажения.
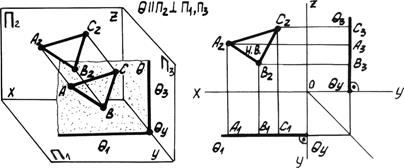
Рис. 4.4б. Фронтальная плоскость уровня.
3. Профильная плоскость уровня параллельна плоскости p3 и перпендикулярна плоскостям p2 и p3 (рис. 4.4в).

Рис. 4.4в. Профильная плоскость уровня.
Фронтальная и горизонтальная проекции плоскости совпадают с её следами Т1 и Т2, которые перпендикулярны оси x. На профильную плоскость p3 любая фигура, расположенная в плоскости Т, проецируется без искажения.
Свойства плоскостей частного положения:
1. Любая геометрическая фигура расположенная в плоскости, перпендикулярной какой-либо плоскости проекций, проецируется на соответствующий след этой плоскости.
2. Любая геометрическая фигура расположенная в плоскости уровня, проецируется без искажения на ту плоскость проекций, которой данная плоскость параллельна.
Источник
1.1.3. Плоскости частного положения
Под плоскостями частного положения понимают такие плоскости, которые перпендикулярны и параллельны плоскостям проекций.
Различают проецирующие плоскости и плоскости уровня.
Проецирующие плоскости – плоскости, проходящие через центр проецирования и перпендикулярные какой-либо плоскости проекций.
Плоскость, перпендикулярная горизонтальной плоскости проекций П1, называется горизонтально проецирующей плоскостью
(рис. 5, а). Плоскости, перпендикулярные фронтальной или профильной плоскости проекций, называют соответственно фронтально или профильно проецирующими (рис. 5, б и в).
Соответствующие следы проецирующих плоскостей обладают собирательным свойством, которое может быть сформулировано следующим образом: любой геометрический элемент, лежащий в проецирующей плоскости, проецируется на вырожденную проекцию плоскости. Так, на рис. 5, а, б и в точки А, В, С и прямые l, a и b, лежащие в плоскостях , β и δ, проецируются на след плоскости на соответствующих плоскостях проекций.
Плоскости уровня – это плоскости, параллельные какой-либо плоскости проекций.
1) горизонтальную плоскость уровня ׀׀ П1 (рис. 6, а);
2) фронтальную плоскость уровня β ׀׀П2 (рис. 6, б);
3) профильную плоскость уровня δ ׀׀ П3 (рис. 6, в).
На той плоскости проекции, к которой параллельна заданная плоскость уровня, любой геометрический элемент, лежащий в ней, проецируется в натуральную величину.
1.1.4. Позиционные задачи
на взаимное пересечение геометрических образов
Задачи на взаимное пересечение связаны с построением точек, принадлежащих одновременно двум рассматриваемым геометрическим образам (двум плоскостям, прямой и плоскости, прямой и поверхности, двум поверхностям).
Две плоскости относительно друг друга могут быть параллельными и пересекающимися.
1.1.4.1. Параллельность плоскостей
Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
На рис. 7 плоскость , заданная двумя пересекающимися прямыми h и f, параллельна плоскости β, заданной следами βП1 и βП2. Согласно определению о параллельности двух плоскостей: h1 ׀׀ h o 1 ( β П1),
1.1.4.2. Пересечение двух плоскостей
Если плоскости не параллельны, то они пересекаются по прямой линии. Построение линии пересечения плоскостей – это первая основная позиционная задача начертательной геометрии на пересечение геометрических образов.
Все задачи на пересечение двух плоскостей можно разбить на две группы:
1) нахождение двух точек, принадлежащих одновременно двум плоскостям. Эти точки определяют искомую линию пересечения плоскостей;
2) определение одной общей точки и направления линии пересечения плоскостей.
1.1.4.3. Пересечение плоскостей общего положения с плоскостью частного положения
Если одна из пересекающихся плоскостей занимает частное положение, то линию пересечения плоскостей находят без дополнительных построений.
На рис.8 плоскость , пересекающаяся с плоскостью, заданной треугольником, занимает горизонтально проецирующее положение. Согласно собирательному свойству проецирующих плоскостей, линия пересечения заданных плоскостей лежит на следе проецирующей плоскости (отрезок 1-2). Поэтому следует только найти фронтальную проекцию линии 1-2, которую определяют по признаку принадлежности прямой плоскости.
Плоскость уровня пересекает любую плоскость по прямой уровня. Горизонтальная плоскость уровня – по горизонтали (рис. 9, а), а фронтальная плоскость уровня – по фронтали (рис. 9, б). В этом случае достаточно определить только одну общую точку и направление линии пересечения плоскостей.
Источник