Способ плоскопараллельного перемещения пирамиды

Способ плоскопараллельного перемещения пирамиды

Название: Способы преобразования проекций — Методические указания (Л.Д. Письменко)

3. решение задач способом плоскопараллельного перемещения

Сущность способа плоскопараллельного перемещения заключает в том, что все точки геометрического образа перемещают во взаимно параллельных плоскостях. Плоскости-носители траекторий перемещения точек параллельны какой-либо плоскости проекций. Траектория – произвольная линия.

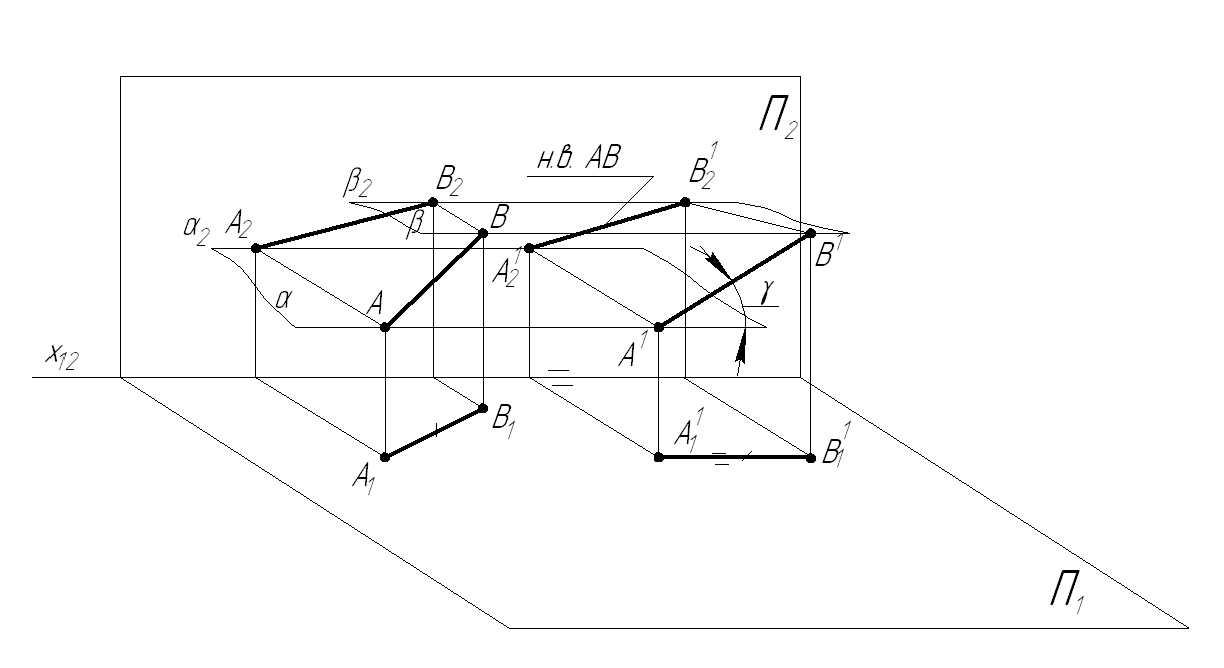
При всяком перемещении точки в плоскости, параллельной плоскости проекций П1 ее фронтальная проекция перемещается по прямой, параллельной оси Х (рис. 4).

Рис. 4. Определение угла наклона α° плоскости треу гольника АВС к плоскости П 1

В случае перемещения точки в плоскости, параллельной П2, ее горизон-

тальная проекция перемещается по прямой, параллельной оси Х (см. рис. 6).

Проследим на конкретных примерах решения задач 1, 2, 3 (см. рис. 5) с использованием способа плоскопараллельного перемещения.

Задача 1 . Определить угол наклона плоскости треугольника ABC к плоскости П1 (или П2) (см. рис. 4).

Чтобы определить угол наклона плоскости треугольника ABC к горизон-

тальной плоскости проекций, необходимо переместить пирамиду SABC плос-

копараллельным движением относительно плоскости П1 так, чтобы основание пирамиды заняло положение фронтально-проецирующей плоскости (α1′′).

Угол наклона вырожденной проекции треугольника ABC на плоскость П2

к оси Х определит искомый угол αо.

Если необходимо определить угол наклона β ° основания пирамиды к

плоскости П2, то пирамиду перемещают плоскопараллельным движением отно-

сительно фронтальной плоскости проекций так, чтобы треугольник ABC занял положение горизонтально−проецирующей плоскости.

1. Строят горизонталь треугольника ABC и перемещают ее относительно плоскости П1 в положение, перпендикулярное к плоскости П2. На черте- же горизонтальная проекция горизонтали h1 ’ перпендикулярна оси Х.

2. Перемещают треугольник ABC относительно плоскости П1 в новое по- ложение — треугольник A1 ’B1 ’C1 ’, когда его горизонталь будет перпен- дикулярна плоскости П2. На чертеже (см. рис. 4) величина горизонталь- ной проекции не изменится, т.е. A1 ’B1 ’C1 ’= A ’B ’C ’.

Фронтальные проекции точек A, B, С – точки A’’, B’’, С’’ перемещают по

прямым, параллельным оси Х. По линиям связи строят фронтальную проекцию основания пирамиды (А1’’В1’’С1’’). На плоскости П2 основание вырождается в отрезок прямой линии A1 ’’B1 ’’C1 ’’. Угол наклона вырожденной проекции (А1’’В1’’С1’’) треугольника ABC к оси Х определяет искомый угол αо.

Задача 2 . Определить расстояние от вершины пирамиды до основания –

треугольника ABC ( рис. 5).

Для решения этой задачи необходимо преобразовать чертеж так, чтобы треугольник ABC – основание пирамиды занял проецирующее положение. В положении, когда основание пирамиды перпендикулярно плоскости П2, отрезок

перпендикуляра, опущенного из точки S1’’ на плоскость α1’’ (A1 B1 C1), опреде-

лит искомую высоту пирамиды m1’’.

1. С помощью циркуля засечками A1’S1’ = A’S’ и C1’S1’= C’S’ строят гори-

зонтальную проекцию вершины пирамиды – точку S1’ и находят ее фрон-

тальную проекцию S1’’.

2. Из точки S1 опускают перпендикуляр m1’’ на плоскость треугольника

A1’’B1’’C1’’ и находят точку встречи перпендикуляра m1’’ с плоскостью.

На чертеже m1’’ ⊥ α1’’ и m1’ ⊥ h1’. Отрезок S1’’K1’’ определяет высоту пи-

рамиды. Отрезок S1’’K1’’ необходимо вернуть в исходное положение.

Задача 3 . Определить натуральную величину основания пирамиды

Чтобы определить натуральную величину основания пирамиды, необхо-

димо двумя последовательно проведенными перемещениями переместить его в новое положение, параллельное плоскости П1, тогда на эту плоскость оно спроецируется без искажения.

1. Располагают вырожденную фронтальную проекцию треугольника A2 B2 C2 — отрезок A2’’ B2’’ C2’’ параллельно оси Х. При этом не изменится величина его фронтальной проекции A2’’ B2’’ C2’’ = A1’’ B1’’ C1’’.

2. Горизонтальную проекцию вершин треугольника A1’B1’С1’ перемеща- ют в новое положение A2’B2’С2’ по прямым, параллельным оси Х. По ли- ниям связи строят горизонтальную проекцию треугольника A2’B2C2’

представляющую натуральную величину основания пирамиды.

Компоновка и выполнение листа 2 с задачами 1, 2, 3 приведены в прило-

Рис. 5. Определение расстояния от вершины S до основания пирамиды ABC

Рис. 6. Определение натуральной величины основания пирамиды

Источник

1.4.3 Способ плоскопараллельного перемещения

Плоско-параллельным перемещением называется такое движение объекта, при котором все его точки перемещаются в плоскостях , параллельных между собой.

При плоскопараллельном перемещении относительно горизонтальной плоскости проекций П₁ все точки объекта перемещаются в горизонтальных плоскостях уровня. При этом горизонтальная проекция объекта по форме и размерам не меняется, изменяется только положение объекта относительно плоскости П₁. Фронтальные проекции точек объекта перемещаются по прямым, параллельным оси проекций х.

При плоскопараллельном перемещении относительно фронтальной плоскости проекций П₂ все точки объекта перемещаются во фронтальных плоскостях уровня при этом фронтальная проекция объекта по форме и размерам не меняется, изменяется только положение объекта относительно плоскости П₂. Горизонтальные проекции точек объекта перемещаются по прямым, параллельным оси проекции х (рисунок 1.4.8).

Рисунок 1.4.8 – Плоско-параллельное перемещение

Рассмотрим примеры преобразования чертежа способом плоскопараллельного перемещения при графическом решении четырех основных задач.

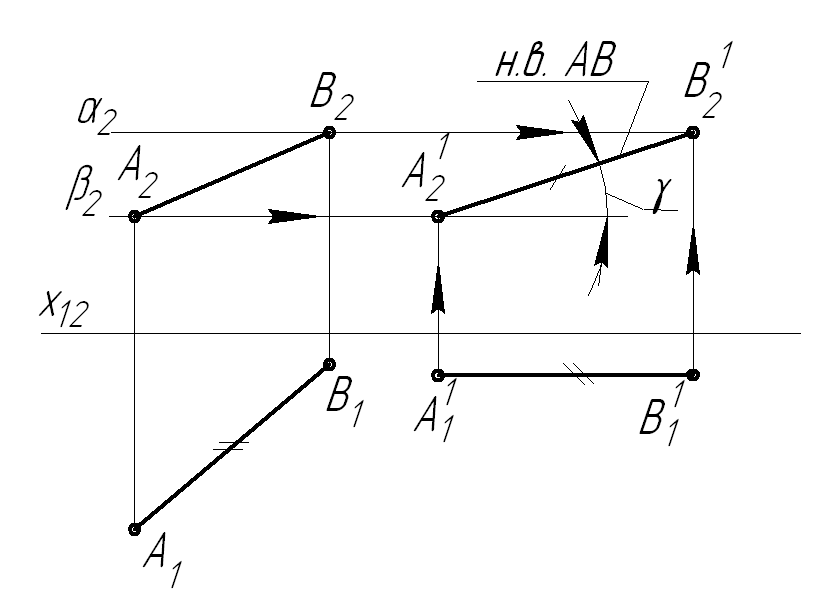
Задача №1. Преобразовать прямую общего положения во фронтальную прямую уровня (рисунок 1.4.9).

Решение. Выполним плоско-параллельное перемещение прямой АВ относительно фронтальной плоскости проекций. Для того, чтобы прямая стала параллельной П₂, горизонтальную проекцию (АВ) А₁В₁ переместим в свободное место чертежа и расположим параллельно оси х. При этом длина отрезка А₁В₁=А₁ 1 В₁ 1 . Фронтальные проекции точек АВ (А₁В₁) перемещаются соответственно по прямым α₂, β₂ – фронтальным проекциям горизонтальных плоскостей уровня α и β, в которых перемещаются точки А и В. Затем перпендикулярно оси х из проекций точек А₁ 1 и В₁ 1 проведем линии связи. Из проекций А₂ и В₂ параллельно оси х проведем линии связи до пересечения с соответствующими линиями связи в соответствии с рисунком 1.4.9. В результате построения определяется натуральная величина АВ и угол γ его наклона к горизонтальной плоскости проекций.

Рисунок 1.4.9 – Решение первой основной задачи способом плоско-параллельного перемещения

Задача №2. Преобразовать прямую общего положения в горизонтально-проецирующую прямую (рисунок 1.4.10).

Решение. Эта задача решается при помощи двух преобразований. Сначала прямую АВ преобразуем во фронтальную прямую уровня (смотри задачу №1), а затем плоскопараллельно переместим прямую АВ относительно фронтальной плоскости проекций и преобразуем в горизонтально проецирующую прямую. Для этого проекцию прямой АВ( А₂ 1 В₂ 1 ) переместим в свободное место чертежа и расположим ее перпендикулярно оси х, не изменяя ее размеров. При этом горизонтальные проекции точек отрезка прямой АВ(А₁ 1 В₁ 1 ) перемещаются по прямой θ₁— горизонтальной проекции фронтальной плоскости уровня θ, в которой перемещаются точки АВ. Определим точку пересечения линий связи проекций точек А₁ 1 ,В₁ 1 и А₂ 1 ,В₂ 1 . Горизонтальная проекция преобразованной прямой проецируется в точку, т.е. прямая АВ преобразилась в горизонтально проецирующую прямую.

Рисунок 1.4.10 – Решение второй основной задачи способом плоско-параллельного перемещения

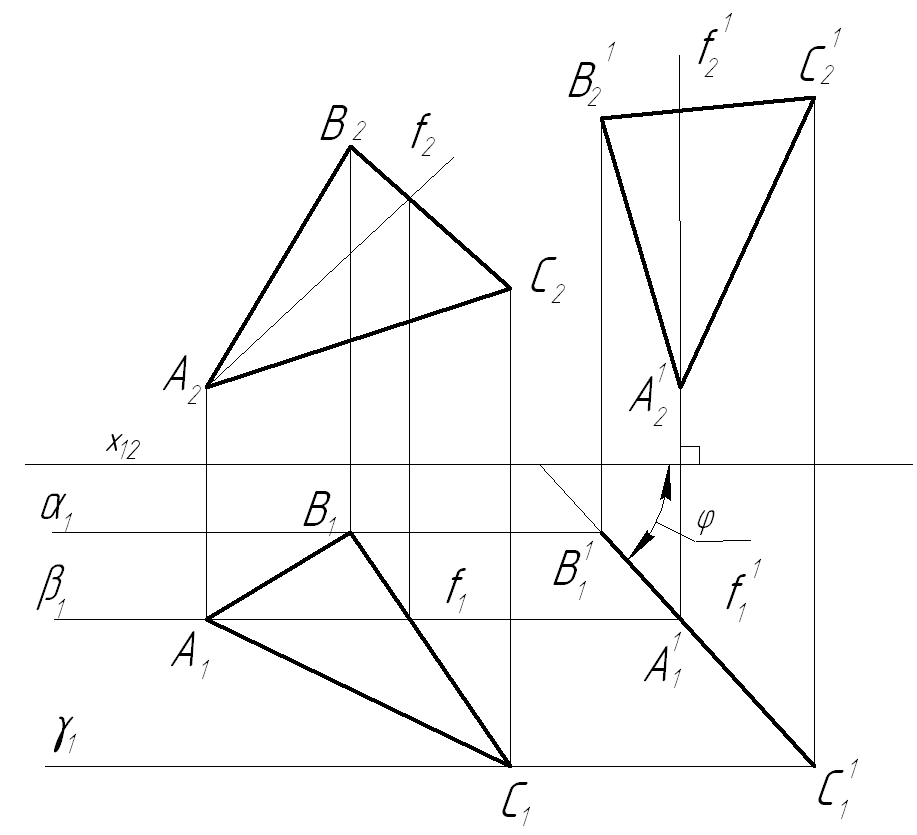
Задача №3. Преобразовать плоскость общего положения во фронтально проецирующую плоскость (Рисунок 1.4.11).

Решение. Плоскость задана треугольником ABC. В плоскости треугольника предварительно построим фронталь f(f₁,f₂). Заметим, если плоскость преобразуется в горизонтально проецирующую, то в плоскости проводиться горизонталь h. Треугольник плоскопараллельно перемещаем таким образом, чтобы фронталь треугольника располагалась перпендикулярно горизонтальной плоскости проекций, то сама фронталь на эту плоскость проецируется в точку, а плоскость треугольника – в прямую, т.е. плоскость треугольника ABC станет горизонтально проецирующей. Поэтому в свободном месте чертежа фронтальную проекцию Δ ABC(A₂B₂C₂) расположим так, чтобы фронтальная проекция фронтали (f₂) располагалась перпендикулярно оси х. При этом фронтальные проекции треугольника не изменили своей формы (A₂B₂C₂= A₂ 1 B₂ 1 C₂ 1 ), а горизонтальные проекции вершин Δ ABC(A₁B₁C₁) переместились по прямым α₁, β₁, γ₁ – горизонтальным проекциям фронтальных плоскостей уровня, проведенных через эти вершины. Фронтальная проекция Δ ABC (A₁ 1 B₁ 1 C₁ 1 ) будет представлять собой отрезок прямой, т.е. плоскость треугольника станет горизонтально проецирующей. При помощи этой задачи также определяется натуральная величина угла наклона φ плоскости Δ ABC к фронтальной плоскости проекций (рисунок 1.4.11).

Рисунок 1.4.11 — Решение третьей основной задачи способом плоско-параллельного перемещения

Рисунок 1.4.12 — Решение четвертой основной задачи способом плоско-параллельного перемещения

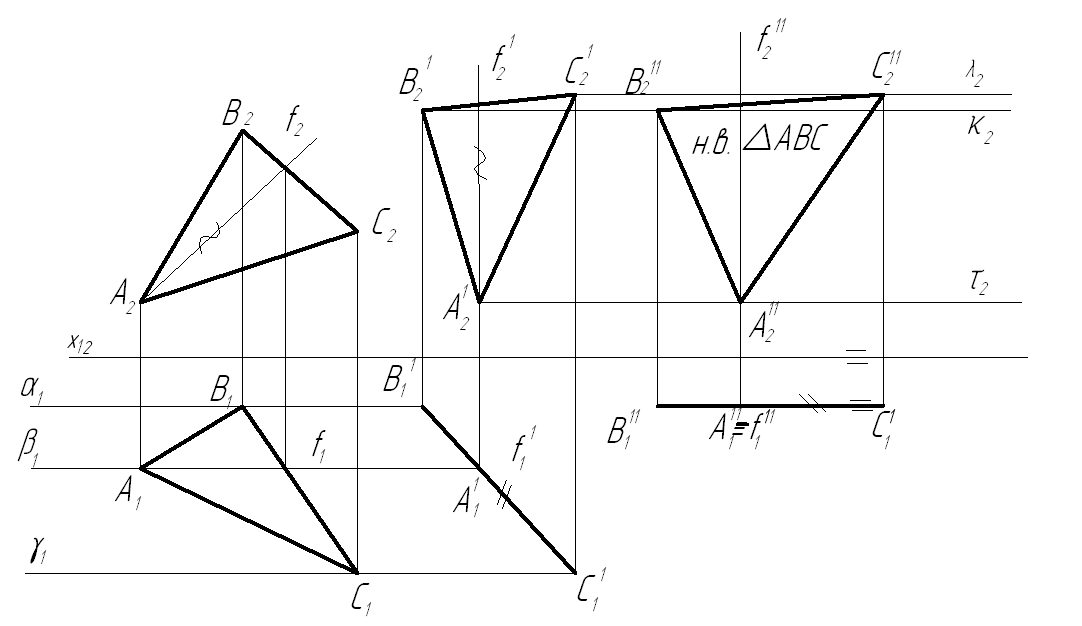
Задача №4. Преобразовать плоскость общего положения во фронтальную плоскость уровня (рисунок 1.4.12).

Решение. Для решения этой задачи необходимо выполнить два преобразования: сначала преобразовать плоскость треугольника во фронтально проецирующую плоскость (смотри задачу №3), а затем преобразовать Δ ABC, чтобы он находился во фронтальной плоскости уровня. Для этого на свободном месте чертежа расположим горизонтальную проекцию Δ ABC(A₁ 1 B₁ 1 C₁ 1 ) параллельно оси х. При этом A₁B₁C₁=A₁ 1 B₁ 1 C₁ 1 , а фронтальные проекции вершин треугольника будут перемещаться по соответствующим плоскостям уровня – λ₂, κ₂, τ₂. Так как преобразованный треугольник лежит в плоскости уровня, следовательно, его фронтальная проекция после последнего преобразования, будет являться натуральной величиной Δ ABC.

Источник

Способ плоскопараллельного перемещения пирамиды

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 145). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

Рисунок 1 45. Определение натуральной величины отрезка методом плоскопараллельного перемещения

а) модель		б) эпюр

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П ₁, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П ₂, её горизонтальная проекция перемещается по прямой параллельной оси х.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой линии — определяющей траекторию перемещения точек, метод плоскопараллельного проецирования имеет следующие частные случаи:

Метод вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости)- метод совмещения.

Источник