Способ плоскопараллельного перемещения определить натуральную величину

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
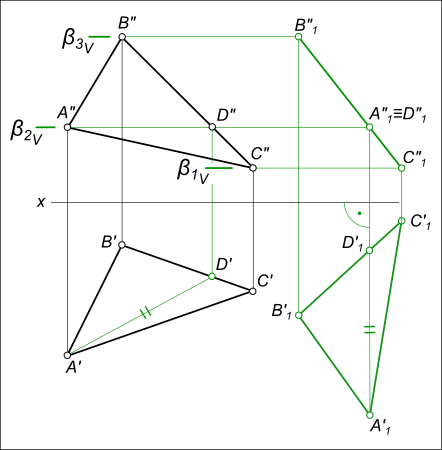
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Источник

57. Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения основан на том, что при параллельном переносе геометрического тела относительно плоскости проекций проекция его на эту плоскость не меняет своей формы и размеров, хотя и меняет положение. При этом если точка перемещается в плоскости, параллельной П₁, то ее фронтальная проекция изображается в виде прямой, параллельной оси П₂/П₁. Если же точка перемещается в плоскости, параллельной П₂, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.

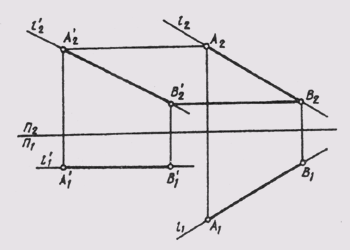
На рис. 107 показан комплексный чертеж прямой АВ. Прямая не параллельна ни одной из плоскостей проекций. Требуется с помощью плоскопараллельного перемещения задать ей такое положение, чтобы она была параллельна одной из плоскостей проекций, например П₂. Через произвольную точку А₁, проводим прямую l₁ параллельную оси П₂/П₁, и от этой точки на прямой откладываем отрезок, равный

А₁В₁. Из точки А₁проводим вертикальную линию связи, а из точки AT, — горизонтальную линию, на пересечении которых и будет новое положение фронтальной проекции А₂‘. Аналогично проведем вертикальную линию связи из точки В₁до пересечения с горизонтальной линией, проведенной из точки B₂. Новое положение фронтальной проекции точки В получим на пересечении этих линий в точке В₂‘.

После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П₂, а значит, спроецировалась она на эту плоскость в натуральную величину.

Применяя метод плоскопараллельного перемещения, можно решать многие задачи, связанные с определением натуральной величины отрезков, углов, плоских фигур, а также заданием им нужного положения. Однако он связан с изменением положения геометрической фигуры в пространстве. В практике же встречаются задачи, при решении которых при преобразовании комплексного чертежа удобнее оставить положение проецирующего тела неизменным, а изменить положение плоскостей проекций.

Источник

Плоскопараллельное перемещение треугольника

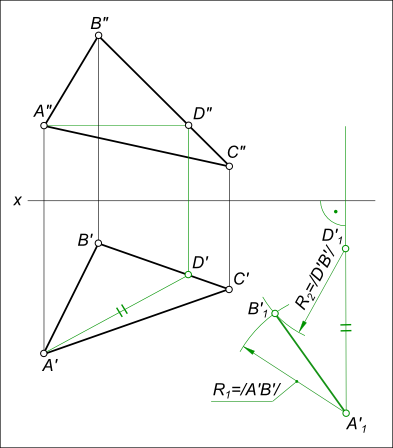
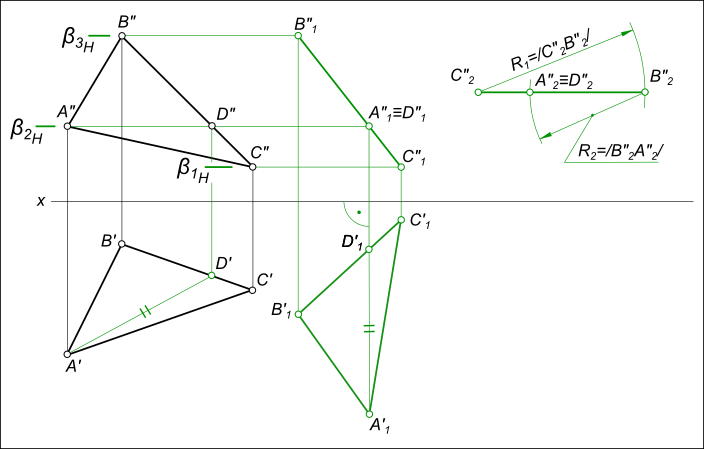
Плоскопараллельное перемещение треугольника ΔABC используемое для преобразования его ортогональных проекций, соответствующих плоскости общего положения δ, в проекции δ₂ // H для получения натуральной величины сторон и углов треугольника ΔABC требует выполнения следующих построений: — горизонтали (или фронтали) плоскости AD;

— перевода горизонтали плоскости в положение A₁D₁ ⊥ V: — на направлении перпендикуляра к плоскости V проведенном на свободном месте чертежа откладываем величину A`D` = A`<sub>1</sub>D`₁ — перестроение других точек проекции ΔA`B`C` на новое положение ΔA`₁B`<sub>1</sub>C`₁: — точку B`<sub>1</sub> дает пересечение дуг R<sub>1</sub> = /A`B`/ и R<sub>2</sub> = /D`B`/; — сторону B`D` продолжим до пересечения

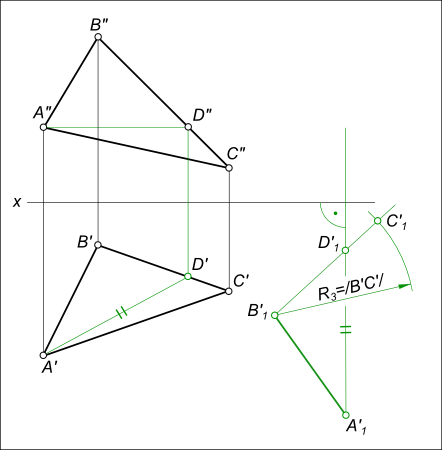
с дугой радиуса R₃ = /B`C`/; — проекции вершин треугольника в новом положении соединяем прямыми линиями;

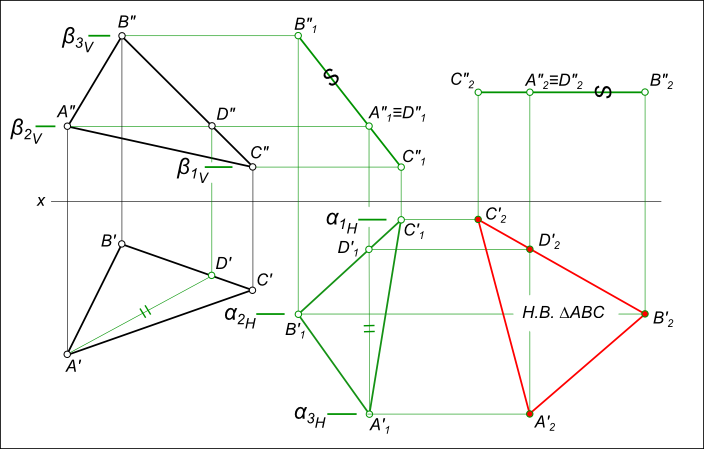
— перемещения фронтальных проекций ΔA»B»C» к новому положению ΔA»₁B»₁C»₁, происходящего в плоскостях уровня β1_V, β2_V и β3_V параллельных плоскости H;

— новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи; — перемещения фронтальной проекции ΔA»₁B»₁C»₁ в положение параллельное H,

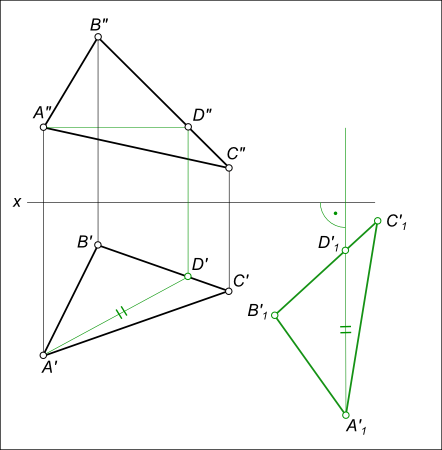
которое выполняем переводом прямой В»₁С»₁ — фронтальной проекции ΔA₁B₁C₁ в положение параллельное оси x: В»₂С»₂ // x; — перемещения горизонтальных проекций ΔA`<sub>1</sub>B`₁C`<sub>1</sub> к новому положению ΔA`₂B`<sub>2</sub>C`₂, происходящего в плоскостях уровня α1_H, α2_H и α3_H параллельных плоскости V;

— новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи: проекция ΔA`<sub>2</sub>B`₂C`₂ соответствует натуральной величине треугольника ΔABC.

Источник

Чертежик

Метки

Натуральная величина треугольника с описанием.

Натуральная величина треугольника определяется 2 методами:

1. замена плоскостей проекции;
2. плоскопараллельное перемещение.

Это задание является обязательным для студентов в учебных заведениях и для его решения необходимо изучить тему: » Способы преобразования чертежа».

Для наглядности я использовал определенное задание и на его примере покажу как находится натуральная величина треугольника.

Алгоритм определения натуральной величины плоскости:

Замена плоскостей проекции

1.) Для построения чертежа использовал задание, расположенное снизу. Первоначально строятся точки по координат в плоскостях П1 и П2.

2.) Строится дополнительная горизонтальная линия 1 1 в верхнем изображении (проводится линия от средне расположенной точки по высоте), затем опускают дополнительные отрезки на нижнее изображение (как указано на рисунке снизу) и соединяют прямой. Эта прямая необходима для того, чтобы на ней расположить вспомогательную плоскость.

3.) Построив прямую на нижнем рисунке, чертится под углом 90 0 ось Х 1 (от точки С1 располагаем на произвольном расстоянии, но не слишком далеко). Затем отмеряются расстояния:

• от С2 до оси Х;
• от В2 до оси Х;
• от А0 до оси Х.

Полученные размеры откладываются от оси Х1 (размеры указаны разными цветами на рисунке снизу) и соединяют, далее подписываются точки.

4.) Строится еще одна дополнительная ось Х2, расположенная параллельно отрезку В 4 С 4 А 4. От точек В4,С4 и А4 проводят прямые перпендикулярные оси Х2.

5.) Отмеряются расстояния:

• от В1 до Х1;
• от С1 до Х1;
• от А1 до Х1.

Полученные результаты измерений откладываются от иси Х2 (на изображении снизу отмечены зелеными и голубым цветами).

6.) Соединяются точки и подписывают полученную плоскость заглавными «Н.В.»

Плоскопараллельное перемещение

7.) Откладывается отрезок на оси Х (обозначен синим цветом).

8.) Переносятся точки на текущее построение.

9.) Соединяют точки, получившиеся при переносе из плоскостей проекций. 10.) Методом вращения точки А2′, С2′ переносятся на горизонтальную прямую, а точка В2′ не меняет свое положение (относительно ее и происходило вращение).11.) Откладывается точка (располагают от оси Х на небольшом расстоянии, т.е. произвольном), относительно которой и будет откладываться плоско параллельное перемещение плоскости. 12.) От точек А2′, С2′ и В2′ опускаются прямые. Далее циркулем необходимо отмерить расстояния:

Затем эти размеры откладываются от С1′ (обозначены красным и синим цветами).

13.) Соединяются и подписываются точки (А1′, В1′ и С1′). Опускают прямые от С2″ и А2″14.) От точек С1 и А1 отводят прямые до пересечения с прямыми опущенными от точек С2″ и А2″. В месте пересечения ставится точка.15.) Завершающим шагом является соединение точек и обводка линиями всего чертежа.Пример чертежа на тему «Натуральная величина треугольника» смотрите здесь.

Источник