Способ плоскопараллельное перемещение прямой

Способ плоскопараллельного перемещения

Способ плоскопараллельного перемещения (переноса) имеет справедливым утверждение, которое может быть выражено в виде следующей теоремы.

При параллельном переносе геометрической фигуры относительно плоскости проекции, проекция фигуры на эту плоскость хотя и меняет свое положение, но остается конгруентной проекции фигуры в ее исходном положении.

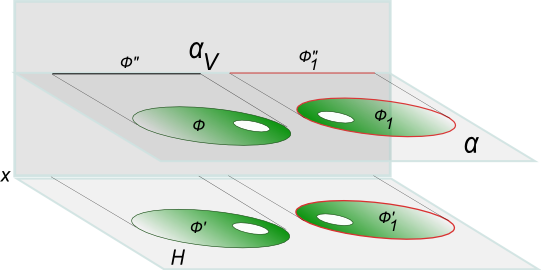
Докажем эту теорему для случая, когда проецируемая фигура Ф плоская, и ее плоскость принадлежит плоскости уровня Ф⊂α, плоскость α║H (рисунок). В этом случае, на основании свойства 6 ортогонального проецирования горизонтальная проекция Ф` будет конгруентна самой фигуре Ф(Ф`≅Ф).

При перемещении фигуры Ф в новое положение Ф₁, фигура Ф`₁ будет конгруентна Ф, так как:

а) расстояние между точками фигуры не меняется;

б) в процессе перемещения фигура Ф все время остается в плоскости α.

В силу параллельности плоскостей α и H, Ф`<sub>1</sub>≅Ф<sub>1</sub>, но Ф<sub>1</sub>≅Ф, а Ф≅Ф`, следовательно Ф`<sub>1</sub>≅Ф`. Данная теорема будет справедлива и в случае, когда геометрическая фигура занимает произвольное (непараллельное) положение относительно плоскости проекции.

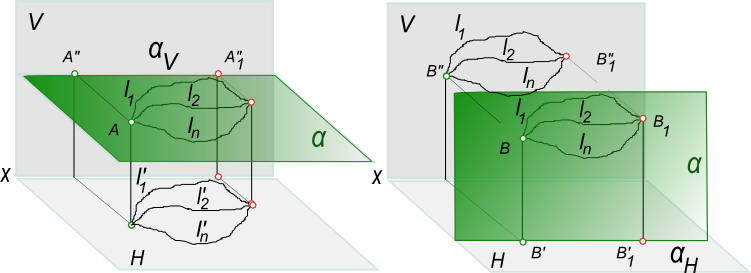
а) При всяком перемещении точки в плоскости, параллельной плоскости проекции H, ее фронтальная проекция перемещается по прямой, параллельной оси x.

б) В случае произвольного перемещения точки в плоскости, параллельной V, ее горизонтальная проекция перемещается по прямой, параллельной оси x.

Пользуясь теоремой и отмеченными свойствами, не составляет труда построить новые проекции геометрической фигуры (по заданным ее ортогональным проекциям), которые соответствуют частным положениям проецируемой фигуры по отношению к плоскости проекции.

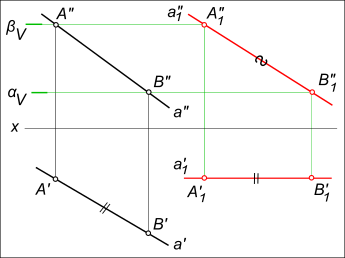
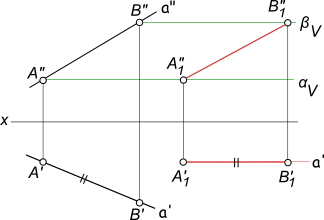
[AB]- отрезок прямой а общего положения перевести в положение параллельное V. Выполняем перемещение отрезка [A`B`] на горизонтальной плоскости проекции в положение параллельное оси x [A₁B₁]. При таком перемещении новая горизонтальная проекция конгруентна исходной [AB]≅[A₁B₁] на основании теоремы.

Фронтальные проекции точек отрезка [A»B»] будут перемещаться в новое положение [A»₁B»₁] в плоскостях α и β параллельных горизонтальной плоскости проекции — по следам α_V и β_V.

Для перевода отрезка прямой общего положения в положение параллельное V требуется одно перемещение отрезка параллельно плоскости проекции H.

Для перевода отрезка прямой из общего положения в проецирующее, необходимо последовательно выполнить два перемещения параллельно плоскостям проекции.

Зная характер геометрических построений, которые необходимо выполнить для перемещения отрезка из общего положения в проецирующее, можно легко перевести плоскость, произвольно расположенную в пространстве, в частное положение (параллельное или перпендикулярное плоскости проекции).

В графической работе №4 используется способ плоскопараллельного перемещения для решение задачи по построению треугольной пирамиды SABC: Графическая работа 4. В графической работе №5 используется способ плоскопараллельного перемещения для решение задачи по по определению наклона ребра SC треугольной пирамиды SABC к плоскости основания ABC: Графическая работа 5. Плоскопараллельное перемещение треугольника, со всеми подробностями, смотри: Плоскопараллельное перемещение треугольника

Источник

Плоскопараллельное перемещение

Плоскопараллельное перемещение — способ перехода от общего положения геометрической фигуры к частному, которое можно осуществить за счет изменения взаимного положения проецируемой фигуры и плоскости проекции путем перемещения в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения в пространстве.

Данный путь лежит в основе метода плоскопараллельного перемещения

Плоскопараллельное перемещение осуществляется путем перемещения геометрической фигуры в новое положение так, чтобы траектория перемещения ее точек находились в параллельных плоскостях. Образно это можно представить в виде перемещения например отрезка вмерзшего в кусок льдины.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой траектории перемещения точек различают:

а) способ параллельного перемещения. Плоскости — носители траекторий перемещения точек параллельны какой-либо плоскости проекции. Траектория — произвольная линия.

б) способ вращения вокруг оси, перпендикулярной к плоскости проекций. Плоскости — носители траектории перемещения точек параллельны плоскости проекции. Траектория — дуга окружности, центр которой находится на оси,перпендикулярной плоскости проекции;

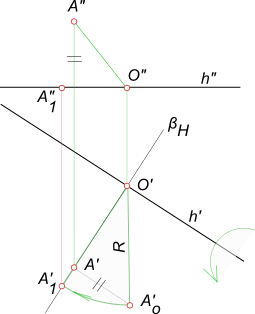
в) способ вращения вокруг оси, параллельной плоскости проекции (вращение вокруг линии уровня);

Плоскости — носители траектории перемещения точек перпендикулярны данной линии уровня. Траектория — дуга окружности, центр которой находится на линии уровня.

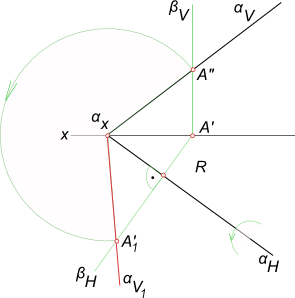
г) способ вращения вокруг оси, принадлежащей плоскости проекции (вращение вокруг следа плоскости);

Плоскости — носители траектории перемещения точек перпендикулярны данному следу плоскости. Траектория — дуга окружности, центр которой находится на следе плоскости.

Источник

Способ плоскопараллельное перемещение прямой

Изменение взаимного положения проецируемого объекта и плоскостей проекций методом плоскопараллельного перемещения осуществляется путем изменения положения геометрического объекта так, чтобы траектория движения её точек находилась в параллельных плоскостях. Плоскости носители траекторий перемещения точек параллельны какой-либо плоскости проекций (рис. 145). Траектория произвольная линия. При параллельном переносе геометрического объекта относительно плоскостей проекций, проекция фигуры хотя и меняет свое положение, но остается конгруэнтной проекции фигуры в ее исходном положении.

Рисунок 1 45. Определение натуральной величины отрезка методом плоскопараллельного перемещения

а) модель		б) эпюр

Свойства плоскопараллельного перемещения:

1. При всяком перемещении точек в плоскости параллельной плоскости П ₁, её фронтальная проекция перемещается по прямой линии, параллельной оси х.

2. В случае произвольного перемещения точки в плоскости параллельной П ₂, её горизонтальная проекция перемещается по прямой параллельной оси х.

В зависимости от положения этих плоскостей по отношению к плоскостям проекций и вида кривой линии — определяющей траекторию перемещения точек, метод плоскопараллельного проецирования имеет следующие частные случаи:

Метод вращения вокруг оси, принадлежащей плоскости проекций (вращение вокруг следа плоскости)- метод совмещения.

Источник

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
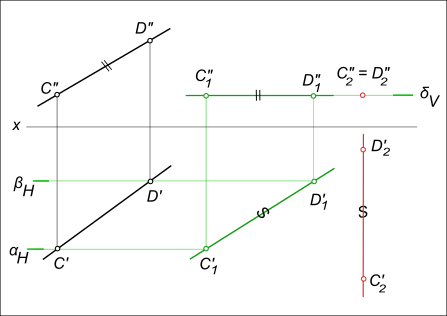
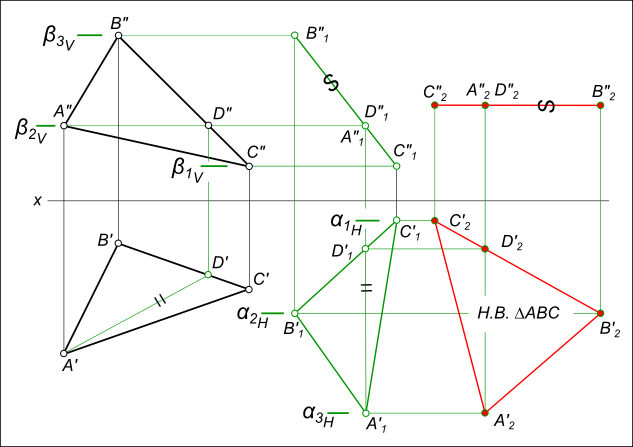
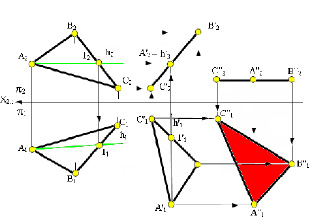
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C» и D», следуя этому свойству, заняли положение C»₁ и D»₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C»₁ и D»₁. Стрелками показано перемещение точек C» и D» параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M»₁N»₁ = M»N» на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M»₂ = N»₂ определяются по линиям связи.

Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A»₁, B»₁, C»₁.
3. Перемещаем проекцию A»₁B»₁C»₁ треугольника ABC в положение A»₂B»₂C»₂, параллельное оси X, соблюдая равенство A»₂B»₂C»₂ = A»₁B»₁C»₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Источник

Научная электронная библиотека

Пиралова О. Ф., Ведякин Ф Ф.,

5.4. Преобразование чертежа способом плоскопараллельного перемещения

Плоскопараллельным называется такое перемещение элемента, при котором все его точки движутся в плоскостях, параллельных одной плоскости, которая принимается за неподвижную.

Обычно за неподвижные плоскости принимаются плоскости проекций. Перемещение производится относительно одной из них. Если одного перемещения недостаточно, то выполняется ещё одно относительно другой плоскости проекций. При плоскопараллельном перемещении геометрического элемента относительно плоскости проекций его проекция на эту плоскость меняет положение, но не меняет своей формы и размеров. Если точка перемещается в плоскости, параллельной П1, то ее фронтальная проекция изображается в виде прямой, параллельной оси П2/П1. Если же точка перемещается в плоскости, параллельной П2, то ее горизонтальная проекция изображается в виде прямой, параллельной той же оси.

Задача 1. Преобразовать прямую общего положения в прямую уровня.

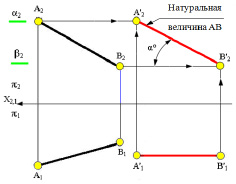
Рассмотрим прямую общего положения АВ, т. е. прямую, расположенную под наклоном ко всем плоскостям проекций (рис. 5.8).

Рис. 5.8. Пример перемещения геометрического элемента (прямая АВ) относительно горизонтальной плоскости проекций

При плоскопараллельном перемещении прямой АВ относительно горизонтальной плоскости проекций все его точки движутся в горизонтальных плоскостях уровня (α и β). Это значит, что отрезок АВ может перемещаться в любое положение, но фронтальные проекции А2, В2 могут перемещаться только по проекциям α2 и β2 горизонтальных плоскостей уровня, линии которых одновременно служат горизонтальными линиями связи. Так как разность высот концов отрезка сохраняется, то угол его наклона к горизонтальной плоскости проекций не меняется и горизонтальная проекция отрезка А1В1 может перемещаться произвольно по отношению к оси Х, сохраняя размеры и форму.

В рассматриваемом примере, отрезок АВ перемещён до положения фронтали. Горизонтальная проекция фронтали на комплексном чертеже должна быть параллельной оси проекций Х. Новая горизонтальная проекция отрезка А’1В’1 расположена правее А1В1 параллельно Х. Из точек А1 и В1 проведены вертикальные линии связи и в пересечении их с горизонтальными линиями связи отмечены новые фронтальные проекции точек А’2 и В’2. Новые проекции [А’1 В’1] → [А’2 В’2] изображают отрезок [АВ] || П2. После преобразования чертежа горизонтальная проекция прямой АВ стала параллельна плоскости П2, а значит, спроецировалась она на эту плоскость в натуральную величину |А’2В’2| = АВ. Угол наклона (α°) прямой к П1 спроецировался на фронтальной плоскости в натуральную величину. Следовательно, первая задача на преобразование комплексного чертежа решена.

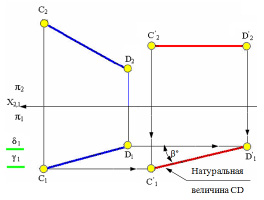
Решим аналогичную задачу относительно фронтальной плоскости проекций П2. Для этого рассмотрим прямую общего положения СD, т. е. прямую, расположенную под наклоном ко всем плоскостям проекций (рис. 5.9).

Рис. 5.9. Пример перемещения геометрического элемента (прямая СD) относительно фронтальной плоскости проекций

При плоскопараллельном перемещении прямой CD относительно фронтальной плоскости проекций все его точки движутся во фронтальных плоскостях уровня (γ и δ).

При этом горизонтальные проекции точек С1и D1 перемещаются по прямым (γ1 и δ1), перпендикулярным вертикальным линиям связи, а фронтальные проекции отрезка C2 D2 могут перемещаться произвольно относительно оси Х, сохраняя свою форму и размеры.

Из точки С1 проводим горизонтальную линию связи, а из точки С׳ 2, — вертикальную линию связи, на пересечении которых и будет новое положение горизонтальной проекции С’1. Аналогично проведем горизонтальную линию связи из точки D1 до пересечения с вертикальной линией связи, проведенной из точки D’2. Новое положение горизонтальной проекции точки Dполучим на пересечении этих линий в точке D’1.

После преобразования чертежа горизонтальная проекция прямой CD стала параллельна плоскости П1, а значит, спроецировалась она на эту плоскость в натуральную величину, а угол наклона прямой к П2 на горизонтальной плоскости проекций тоже спроецировался в натуральную величину т.е. в результате получено ещё одно решение первой задачи на преобразование комплексного чертежа.

Решим вторую задачу на преобразование комплексного чертежа.

Задача 2. Преобразовать прямую общего положения в проецирующую прямую.

Для решения такой задачи необходимо выполнить два преобразования комплексного чертежа.

Если объект (например, прямые АВ или СD) расположен относительно плоскостей проекций в общем положении (наклонен по отношению к плоскостям проекций под углами отличными от 90°), необходимо выполнить первое преобразование – переместить объект в положение, параллельное одной из плоскостей проекций, т. е. решить первую задачу на преобразование, а затем выполнить второе преобразование комплексного чертежа – натуральную величину прямой расположить перпендикулярно плоскости проекций, т.е. преобразовать параллельное положение прямой относительно плоскости проекций в перпендикулярное (проецирующее).

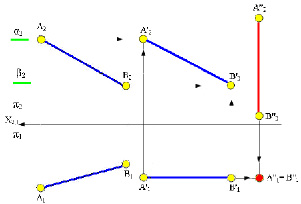
Рассмотрим решение второй позиционной задачи на примере прямой (АВ) общего положения (рис. 5.10).

Первая ступень решения – прямую общего положения АВ переместить до положения фронтали А’1В’1. При решении необходимо помнить, что А1В1= А’1В’1. Вторая ступень решения – прямую АВ из положения фронтали переместить в положение горизонтально-проецирующей прямой А»2В»2. В этом случае при построении необходимо помнить, что А’1В’1 = А»2В»2 и горизонтально проецирующая прямая перпендикулярна горизонтальной плоскости проекций, а на комплексном чертеже А»2В»2 ⊥ х.

Рис. 5.10. Пример преобразования прямой общего положения
в положение горизонтально-проецирующей

При решении третьей позиционной задачи необходимо преобразовать комплексный чертеж так, чтобы плоскость общего положения стала проецирующей.

Задача 3. Преобразовать плоскость общего положения Δ(АВС) в проецирующую плоскость.

Для решения задачи выбрана плоскость общего положения, заданная двумя проекциями А1В1С1 и А2В2С2 (рис. 5.11). При решении необходимо помнить и использовать два положения:

— две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой плоскости;

— прямую линию уровня можно одним преобразованием сделать проецирующей (перпендикулярной) к одной из плоскостей проекций.

Первая ступень решения – построить во фронтальной плоскости треугольника фронтальную проекцию горизонтали h2, а затем горизонтальную проекцию горизонтали h1.

Рис. 5.11. Преобразование плоскости общего положения в проецирующую

Вторая ступень решения – переместить горизонтальную проекцию плоскости треугольника таким образом, чтобы горизонтальная проекция горизонтали стала фронтально проецирующей прямой. Для этого в любом удобном для построения месте построить h’1 и на этой прямой отложить величину А’11’1=А111, На этом отрезке построить треугольник А’1В’1С’1 = А1В1С1 таким образом, чтобы обход вершин осуществлялся в одном направлении. Для чего необходимо провести дуги окружностей из точки 1’1 радиусом 1’1С’1 = 11С1, а из точки А’1, радиусом А’1С’1. В пересечении построенных дуг обозначить точку С’1, с учётом направления обхода вершин. Провести прямую 1’1С’1 и на ней отложить прямую линию С’1В’1 = С1В1. Положение вершин определено. Нужно соединить вершину А’1 с вершинами В’1 и С’1.

Третья ступень решения. По линиям связи построить фронтальную проекцию плоскости треугольника А’2В’2С’2. Для этого из точки С’1 провести вертикальную линию связи до пересечения с горизонтальной линией связи из точки С2. В пересечении горизонтальной и вертикальной линий связи получится С’2. Из точки А’1 провести вертикальную линию связи, а из А2 провести горизонтальную линию связи. В пересечении указанных линий получится А’2. Аналогичным способом построить В’2. Соединить полученные проекции точек. В результате получается фронтально проецирующая плоскость. Значит, решена третья позиционная задача.

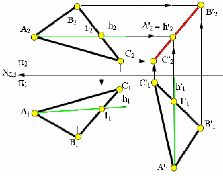
Задача 4.Преобразовать комплексный чертеж плоскости общего положения в плоскость уровня (рис. 5.12).

Рис. 5.12. Пример решения четвёртой позиционной задачи способом плоскопараллельного перемещения

Четвёртую позиционную задачу относительно плоскости общего положения нельзя решить без решения третьей позиционной задачи. Для решения четвёртой задачи необходимо выполнить два перемещения заданной плоскости относительно плоскостей проекций.

Учитывая имеющееся решение третьей задачи. Рассмотрим пример решения четвертой задачи на основе решения предыдущей (третьей) задачи. Решаем четвёртую позиционную задачу, перемещая фигуру относительно фронтальной плоскости проекций до положения плоскости треугольника А»2В»2С»2 ⊥ С’1С’2. В таком положении плоскость находится параллельно горизонтальной плоскости проекций т.е. плоскость становится плоскостью горизонтального уровня.

Горизонтальная проекция А»1В»1С»1 плоскости определяется в пересечениях вертикальных линий связи с горизонтальными. Недостатком способа плоскопараллельного перемещения является необходимость построения свободно перемещаемой проекции в новом положении. Достоинством этого способа можно считать возможность удобного размещения новых проекций на комплексном чертеже.

Источник