Нормализованная запись числа
Нормализованная запись отличного от нуля действительного числа – это запись вида Где q – целое число (положительное, отрицательное или ноль) m – правильная Р-ичная дробь, у которой первая цифра после запятой не равна нулю, то есть: Примеры записи десятичных чисел: Примеры записи двоичных чисел: Умножением двоичных чисел мы пока не занимались, поэтому вам может быть не понятно, почему 1 = 0,1 * 2 1 . Объяснять подробности здесь не будем, просто имейте ввиду, что в двоичной системе умножение на два в какой-либо степени – это сдвиг разрядов. Если число умножается на 2 в какой-то степени, и если эта степень – целое положительное число, то это будет сдвиг влево на количество разрядов, которое соответствует степени числа два. То есть Как нетрудно догадаться, деление – это сдвиг вправо. Например,
Число НОЛЬ не может быть записано в нормализованной форме в том виде, в котором мы её определили. Поэтому считаем, что нормализованная запись нуля в десятичной системе будет такой:
Нормализованная экспоненциальная запись числа – это запись вида Где q – целое число (положительное, отрицательное или ноль) m – правильная Р-ичная дробь, у которой целая часть состоит из одной цифры, при этом m – это мантисса числа, а q – порядок (или экспонента) числа.
Описанные выше примеры в нормализованной экспоненциальной записи будут выглядеть так, как показано ниже.
Примеры записи десятичных чисел: Примеры записи двоичных чисел: Обратите внимание, что в нормализованной форме первая цифра после запятой НЕ может быть нулём, а в нормализованной экспоненциальной форме это допускается.
Источник
Способ перевода нормализованных чисел
На этом шаге мы рассмотрим преобразование нормализованных чисел. .
Вещественное число X может быть представлено в двух формах — естественной и нормализованной . В естественной форме у X имеется целая и дробная части, между которыми помещается разделитель (запятая или точка), например, 123,4567. Однако такая запись неудобна для слишком больших или, наоборот, слишком малых чисел. Кроме того, использование такой формы (она называется также «представление числа с фиксированной запятой») в компьютере вызвало бы снижение точности вычислений из-за необходимости приведения в соответствие разрядов обрабатываемых чисел и связанных с этим округлений или могло бы породить ситуацию, называемую переполнением, когда старший разряд числа не умещается в отведенной разрядной сетке. По указанным причинам вещественные числа в компьютере представляются в нормализованном виде (другое название — «представление числа с плавающей запятой»), главным достоинством которой является автоматическое масштабирование числа на каждом этапе обработки, что, с одной стороны, обеспечивает максимально возможную точность вычислений, а с другой — избавляет от необходимости принимать меры по предотвращению переполнения (за исключением достаточно экзотических ситуаций с выходом числа за отведенную разрядную сетку). По сути, это универсальная форма записи всех чисел, кроме определенных как «тип: целые» (например, Integer, Word или Byte в PASCAL ‘е).
Сначала познакомимся с необходимыми понятиями применительно к десятичной системе счисления.
Число X 10 называется нормализованным, если оно представлено в виде
X 10 = [+|-] M 10 · 10 [+|-] k 10
В этой записи M10 называется мантиссой нормализованного числа; значения мантиссы лежат в интервале 0,1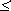 
M 10 k 10 называется порядком нормализованного числа — это целое положительное десятичное число. Примеры: — 123410 = — 0,1234·10 4 ; 0,0345610 = 0,3456·10 -1 .
Понятие нормализованного числа следует отличать от понятия числа в нормальной форме; данная форма достаточно часто используется при записи чисел в математике, физике, технических дисциплинах и отличается от нормализованного представления тем, что мантисса лежит в интервале 1 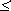M 10 kБ=1,38·10 -23 .
При нормализации происходит расчленение «составляющих» числа с выделением знака числа, мантиссы, знака порядка и порядка — как будет показано ниже, это создает определенные удобства при хранении и обработке чисел в компьютере.
Аналогично нормализации десятичного числа можно в нормализованной форме представить и число в произвольной системе счисления p :
При этом значения мантиссы лежат в интервале p -1 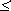Mp (т.е. первая значащая цифра мантиссы всегда ненулевая), а показатель степени представляется в системе p (kp) . Например, для p = 2:
Мантисса располагается в промежутке 0,12 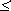M 2 M 10 Рис.1. Алгоритм нормализации
Подобно задаче о преобразовании целых и дробных чисел, можно поставить задачу о преобразовании представления числа в нормализованной форме в системе счисления p к нормализованному представлению в системе q . Практическое значение такого преобразование состоит в том, что, как было сказано, в компьютере все вещественные числа хранятся и обрабатываются в нормализованном двоичном представлении и, следовательно, при их вводе осуществляется перевод X10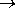 
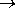
X2 , а при выводе — обратный перевод X2 X10 . Однако прежде, чем обсуждать такой перевод, необходимо рассмотреть, как производится преобразование вещественного числа из естественной формы к нормализованному виду.
При нормализации различаются ситуации Xp>1 и Xp -1 . В первом случае для нормализации необходимо перемещать разделитель разрядов влево по числу до тех пор, пока не исчезнет целая часть числа, но первая цифра после разделителя будет ненулевой; каждое перемещение разделителя на 1 разряд влево эквивалентно делению числа на p и, чтобы число не менялось, показатель должен возрастать на 1 при каждом сдвиге. Если обозначить эту операцию N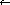 
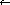
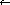
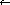
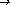
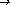
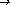
(будем называть ее «нормализация влево»), то N [(123,45)10] = 0,1234510·10 3 ; N [(23,4·10 5 )10] = 0,23410·10 7 ; N [(1212,2)3] = 0,121223·3 11 . Аналогично можно ввести операцию «нормализация вправо» (N
) , обеспечивающая нормализацию чисел меньших p -1 ; очевидно, такие числа необходимо умножать на p с одновременным уменьшением показателя на 1 до тех пор, пока первая цифра после разделителя станет ненулевой. Например, N[(0,000101·2 -101 )2] = 0,101·2 -1000 ; N[(0,000987)10] = 0,98710·10 -3 . Общий алгоритм нормализации можно изобразить в виде блок-схемы на рисунке 1.
При практической реализации данного алгоритма не следует забывать, что изменение значения kp на 1 должно производиться по правилам арифметики системы счисления p . В дальнейшем при необходимости проведения нормализации в ходе каких-либо преобразований будем просто ссылаться на приведенный алгоритм как готовый модуль.
Вернемся к задаче перевода нормализованного числа из одной системы счисления в другую. Пусть, имеется число Xp = [+|-]Mp · p [+|-]kp , для которого необходимо найти соответствующее ему Xq = [+|-] Mq · q [+|-]kq . Представляется достаточно очевидным, что преобразование не затронет знаков мантиссы и показателя степени. Таким образом, для осуществления преобразования необходимо установить соответствие между (Mp, kp) и (Mq, kq) . Оно получается достаточно просто, исходя из того, что Xp = Xq , откуда следует:
(13)
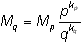
Из (13) вытекает, что для осуществления преобразования можно Mp умножить на p kp , т.е. перейти к естественной форме числа в системе p , перевести его в систему q , а затем нормализовать. Однако в таком варианте действий теряется точность числа и возможно переполнение на промежуточных этапах преобразования. Во избежание этого необходимо чередовать умножение (или деление) на p и нормализацию по основанию q . При этом, поскольку все операции выполняются по правилам арифметики в системы p , будут получены не (Mq ,kq) в окончательном варианте, а их представления в системе p — обозначим их (Mq)p и (kq)p , которые затем нужно будет перевести в систему q . Различаются также ситуации kp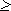 
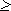
0 и kp — в первом случае необходимо умножать начальное и промежуточные значения мантиссы на p и для нормализации делить на q , во втором — наоборот. Каждый раз при умножении или делении на p показатель kp будет менять свой значение на 1; продолжать действия следует до тех пор, пока не выполнится условие kp= 0 . Алгоритм действий для ситуации kp 0 представлен на рисунке 2.
Рис.2. Алгоритм действий для ситуации kp 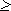0
Пример 8. Выполнить преобразование X 10 =16,510 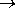X 2 .
Перевод можно осуществить отдельно для целой и дробной части, а затем их объединить — для нас этот результат послужит эталоном для проверки нового алгоритма. Легко получить, что 16 10 = 10000 2 , а 0,5 10 = 0,1 2 ; следовательно, 16,5 10 = 10000,1 2 = (0,100001·2 101 ) 2 .
Алгоритм Real_1 начинает функционировать после нормализации исходного числа; для этой цели можно воспользоваться алгоритмом Norma ; в результате начальными значениями будут M 10 = 0,165; k 10 = 2. Результаты операций будем заносить в таблицу:
Окончательно имеем: X 2 = (0,100001·2 101 ) 2 .
Подобным же будет алгоритм преобразования X10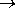X2 и при kp .
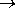
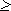
Последовательность действий при обратном переводе X2X10 отчасти противоположна только что рассмотренной; для kp 0 она представлена в виде блок-схемы на рисунке 3. Нормализация в конце (после k =0) производится при необходимости.
Рис.3. Последовательность действий при обратном переводе
Пример 9. Выполнить преобразование: X 2 = (0,11·2 110 ) 2 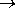X 10 .
Для контроля результата: 0,11 2 =0,75 10 ; (2 110 ) 2 =(2 6 ) 10 =64; следовательно, (0,11·2 110 ) 2 =0,75·64=48 10 . Для преобразования воспользуемся построенным алгоритмом Real_2 (рис. 3). Промежуточные результаты снова будем заносить в таблицу:
Таким образом, получаем: (0,11·2 110 ) 2 =0,48·102=48.
Как и в предыдущем преобразовании, алгоритм в случае k p будет отличаться только тем, что число в процессе перевода необходимо делить на q и умножать на p .
Со следующего шага мы начнем рассматривать кодирование чисел в компьютере и действия над ними .
Источник
Кодирование вещественных чисел. Нормализованное представление числа
В компьютерной технике вещественными называются числа, имеющие дробную часть.
Дробные числа могут содержать большой набор цифр. Например: 0.0000345 или 10900000 (т.е очень большие или очень маленькие числа). Для удобства вещественные числа приводят к виду так называемого нормализованного представления числа. Заключается такое представление в том, что число записывается в виде произведения на основание системы счисления, возведенное в ту или иную степень. Например, предыдущие два числа в нормализованном виде будут выглядеть так: 0.345 * 10 -4 и 0.109 * 10 8 . Здесь числа 0.345 и 0.109 – мантиссы вещественных чисел, 10 – основание системы счисления, а -4 и 8 – порядки. При этом запятая (точка), разделяющая дробную и целую части ставится перед первой значащей цифрой (отличной от 0).
Нормализованная форма числа является наиболее удобной для представления дробных чисел в компьютере.
Понятно, что нормализированное представление используется не только для десятичной системы счисления. Вот примеры нормализованных записей дробных чисел в двоичной системе счисления:
101.11 = 0.10111 * 2 11
0.001 = 0.1 * 2 -10
Здесь степени 11 и 10 – это двоичная форма десятичных чисел 3 и 2.
Нормализованная форма представления числа – это одна из форм множества вариантов экспоненциальной формы записи числа.
Пусть слово состоит из 2 байт, два слова – это 4 байта или 32 бита.
Нормализированное число одинарной точности, представленное в формате с плавающей точкой, записывается в память следующим образом: знак числа – в бите 15 первого слова (0 – для положительных и 1 – для отрицательных чисел); порядок размещается в битах 7-14 первого слова, а мантисса занимает остальные 23 бита в двух словах (с 0 по 6 бит первого слова и все биты второго слова). Нормализированное число двойной точности записывается в четыре слова памяти и отличается от представления чисел с одинарной точностью только тем, что продолжение мантиссы размещается в следующих за первым словом трех последовательных словах памяти, а всего под мантиссу в этом случае отводится 55 бит.
Порядок числа, представленного в формате с плавающей точкой, изменяется в диапазоне от -128 до +127 и запоминается увеличенным на 128. Такой способ представления порядка называется смещенным.
Следует иметь в виду, что, хотя для мантиссы отведено 23 разряда для чисел одинарной точности и 55 разрядов – для чисел двойной точности, в операциях участвует 24 и 56 разрядов соответственно, т.к. старший разряд мантиссы нормализированного числа не хранится, т.е. имеет место так называемый скрытый разряд. Однако при аппаратном выполнении операций этот разряд автоматически восстанавливается и учитывается. Порядок числа также учитывает скрытый старший разряд мантиссы.
Нормализованная мантисса в двоичной системе счисления всегда представляется десятичным числом m , лежащим в диапазоне 0,5 .
Пример представления числа в формате с плавающей точкой:
Если мантисса представлена бесконечной периодической дробью, то последний учитываемый разряд мантиссы округляется.
При выполнении арифметических операций над числами, представленными в формате с плавающей точкой, надо отдельно выполнять их для порядков и мантисс. При алгебраическом сложении чисел надо сначала уравнять порядки слагаемых. При умножении порядки надо складывать, а мантиссы — перемножать. При делении из порядка делимого вычитают порядок делителя, а над мантиссами совершают обычную операцию деления. После выполнения операций, если это необходимо, проводят нормализацию результата, что влечет изменение порядков, т.к. каждый сдвиг на один разряд влево соответствует уменьшению порядка на единицу, а сдвиг вправо увеличению на единицу. Введение термина «плавающая точка» как раз и объясняется тем, что двоичный порядок, определяющий фактическое положение точки в изображении числа, корректируется после выполнения каждой арифметической операции, т.е. точка в изображении числа «плавает» (изменяется ее положение) по мере изменения данной величины. А в изображении чисел, представленных в формате с фиксированной точкой, она жестко зафиксирована в определенном месте.
Арифметические операции с числами, представленными в формате с плавающей точкой, намного сложнее таких же операций для чисел, представленных в формате с фиксированной точкой. Но зато плавающая точка позволяет производить операции масштабирования автоматически в самой машине и избавляет от накопления абсолютной погрешности при вычислениях (хотя не избавляет от накопления относительной погрешности).
Источник
