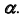- Пересечение прямой с плоскостью
- 61. Пересечение прямой с плоскостью
- Пересечение прямой с плоскостью в начертательной геометрии с примерами
- Пересечение проецирующей прямой с плоскостью общего положения
- Пересечение прямой общего положения с проецирующей плоскостью
- Пересечение прямой общего положения с плоскостью общего положения
Пересечение прямой с плоскостью
Задача на пересечение прямой с плоскостью — это одна из основных задач, с ее применением сталкиваются при рассмотрении сечения тел плоскостями и пересечения поверхностей.
Нахождение точки встречи прямой с плоскостью, заданной пересекающимися прямыми
Плоскость и пересекающая ее прямая занимают общее положение.
(γ ∩ α) = l — прямая, пересекающаяся с прямой b.
На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :
1) проводим через b` горизонтальный след γH — горизонтально-проецирующей плоскости γ;
2) определяем фронтальную проекцию линии пересечения l, вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γH пересекает прямые c` и d`;
3) определяем точку K»=l»∩b». Зная K», находим K` на пересечении b` с линией проекционной связи.
Нахождение точки встречи прямой с плоскостью, заданной параллельными прямыми
Задача по нахождению точки встречи прямой с плоскостью заданной следами.
Алгоритм решения не меняется, если плоскость будет задана параллельными прямыми или прямыми, по которым она пересекает плоскости проекций (следы плоскости).
При решении задач на пересечение прямой с плоскостью в качестве вспомогательных плоскостей применяют проецирующие плоскости. Но в случае, например, профильной прямой они бесполезны и тогда надо применить плоскость общего положения.
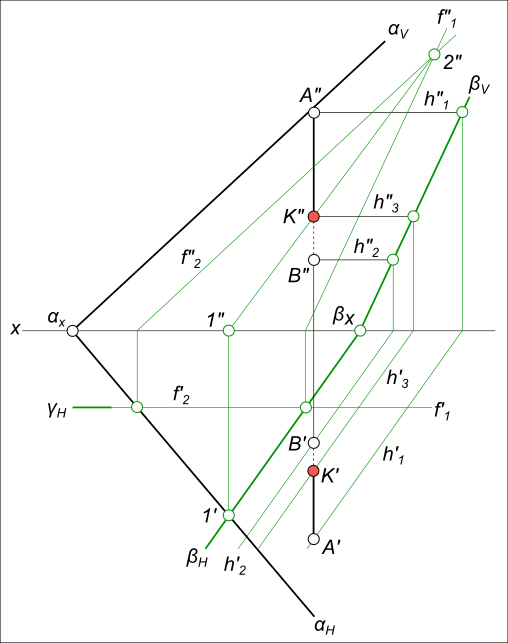
Найти точку встречи профильной прямой AB с плоскостью α заданной следами
Алгоритм выполнения геометрических построений: 1) Заключаем отрезок AB во вспомогательную секущую плоскость общего положения β; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости β с данной плоскостью α; 3) Определяем проекцию K» точки K на пересечении 1″-2″ с прямой A»B». Проекция K` точки K может быть найдена: — на пересечении A`B` с 1`-2`; — или как принадлежащая плоскостям α и β.
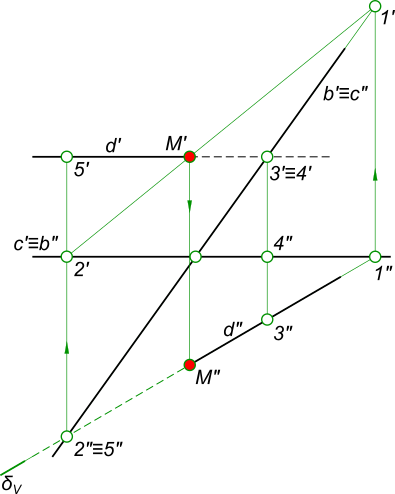
Найти точку встречи прямой d с плоскостью α(b, c), определить видимость
Алгоритм выполнения геометрических построений: 1) Заключаем прямую d во вспомогательную секущую фронтально проецирующую плоскость δ; 2) Определяем проекции линии пересечения 1-2, вспомогательной секущей плоскости δ с данной плоскостью α; 3) Определяем проекцию K` точки K на пересечении 1`-2` с прямой d`. Проекцию K» точки K находим в пересечении d» с линией проекционной связи.
Данный способ решения задачи — найти точку встречи профильной прямой с плоскостью заданной следами применен в статье: Сечение пирамиды плоскостью
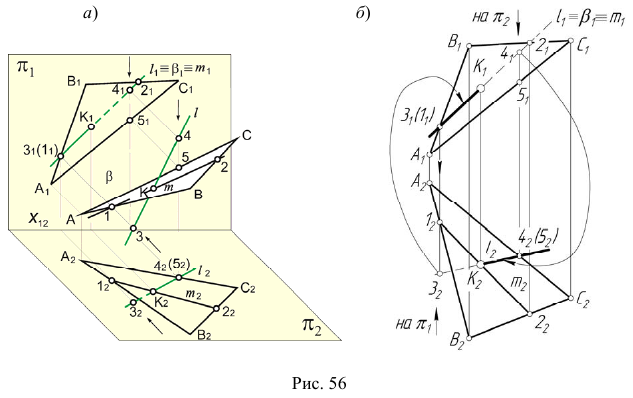
Определение видимости пересечения прямой с плоскостью на плоскостях проекций выполняем, используя Конкурирующие точки 2, 3 и 4, 5.
Источник
61. Пересечение прямой с плоскостью
§ 61. Пересечение прямой с плоскостью
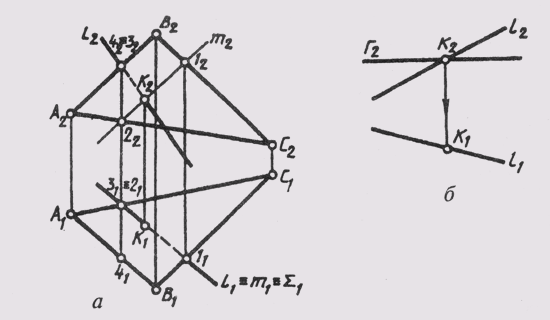
Прямая пересекает плоскость в одной точке. Точку пересечения прямой с плоскостью определяют путем построения вспомогательной прямой линии, лежащей в одной проецирующей плоскости с заданной прямой. На рис. 119, а приведен комплексный чертеж прямой l и плоскости 9 (ABC), причем т
Q (ABC). Через горизонтальную проекцию прямой l1 проводим проекцию вспомогательной горизонтально проецирующей плоскости Sum1. В пересечении плоскостей Q и Sum получаем линию т, то есть т =Sum ^ Q. Горизонтальная проекция прямой т определяется горизонтальными проекциями точек 1 и 2 пересечения линий ЕС и АС со вспомогательной плоскостью Sum , то есть В1С1 ^ Sum = l1; А1С1 ^ Sum1=21; т1 = l1^21.
Для получения фронтальной проекции линии l построим фронтальные проекции точек 1 и 2, соединив которые, получим фронтальную проекцию m2. В пересечении фронтальных проекций прямых т и l получим фронтальную проекцию точки К, принадлежащей и прямой l, и прямой т, лежащей в плоскости Sum. Значит, точка К и принадлежит плоскости Sum, и является точкой пересечения прямой l с плоскорью Sum.
Видимость прямой и плоскости относительно горизонтальной плоскости проекций определяется с помощью горизонтально конкурирующих точек 2 и 3, а видимость относительно фронтальной плоскости проекции — с помощью фронтально конкурирующих точек 3 и 4.
Если плоскость занимает частное положение, то одна проекция точки пересечения прямой с плоскостью определяется сразу в пересечении вырожденной проекции плоскости с соответствующей проекцией прямой (рис. 119, б).
Если прямая пересекает плоскость под прямым углом, то на комплексном чертеже проекции этой прямой располагаются перпендикулярно проекциям соответствующих линий уровня плоскости на основании теоремы о проецировании прямого угла (см. § 29).
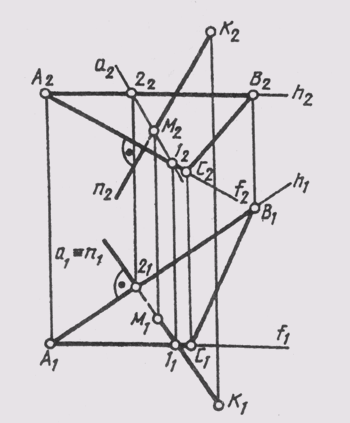
На рис. 120 построены проекции основания М перпендикуляра п, проведенного к плоскости 9 (ABC) из точки К пространства. В AВС имеем: АВ — горизонталь (A2B2 _|_ A2A1), AC — фронталь (А1С1 _|_A1A2). Поэтому проекции перпендикуляра n э К располагаются: п1 _|_A1B1и n2 _|_ А2С2. Основание перпендикуляра на плоскости построено с помощью вспомогательной линии а плоскости, лежащей в одной с перпендикуляром п горизонтально проецирующей плоскости (а ^ п = М).
Если прямая пересекает плоскость в бесконечности, то имеет место параллельность прямой с плоскостью. На рис. 121 построена прямая т, проходящая через точку N u параллельная плоскости треугольника KLM. На комплексном чертеже параллельность прямой и плоскости доказывается тем, что m1 || а1и m2|| а2; a
Источник
Пересечение прямой с плоскостью в начертательной геометрии с примерами
Содержание:
Пересечение прямой с плоскостью:
Рассмотрим три варианта, а соответственно и три алгоритма решения задачи по определению точки пересечения прямой с плоскостью:
- прямая — проецирующая, плоскость — общего положения;
- прямая — общего положения, плоскость — проецирующая;
- прямая и плоскость — общего положения.
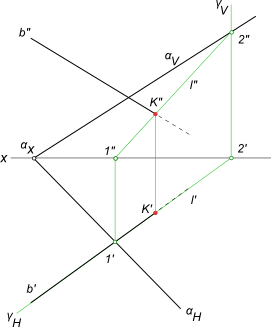
Пересечение проецирующей прямой с плоскостью общего положения
При решении задач на определение точки пересечения проецирую- щей прямой с плоскостью общего положения используется собирательное свойство вырожденной проекции проецирующей прямой. Вырожденная проекция прямой совпадает с одноименной проекцией искомой точки. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной плоскости.
Задача:
На эпюре Монжа построить проекции точки пересечения проецирующей прямой
Алгоритм решения
- Так как прямая
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
Отметим горизонтальную проекцию
- Фронтальную проекцию
определим по принадлежности точки K плоскости
(задача 3).
Видимость прямой 
Пересечение прямой общего положения с проецирующей плоскостью
При решении задач на определение точки пересечения проецирующей плоскости с прямой общего положения используется собирательное свойство вырожденной проекции проецирующей плоскости. Одна из проекций искомой точки определяется на пересечении вырожденной проекции плоскости с одноименной проекцией заданной прямой. Другая проекция точки пересечения прямой с плоскостью определяется по принадлежности точки заданной прямой.
Задача:
На эпюре Монжа построить проекции точки пересечения прямой общего положения 
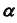
Алгоритм решения
- Так как точка K — общий элемент прямой и плоскости, а плоскость
— фронтально- проецирующая, следовательно, проекция
определится на пересечении фронтальных проекций прямой и плоскости
- Горизонтальную проекцию
определим по принадлежности точки K прямой
(задача 1).
Видимость прямой 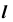
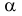
Пересечение прямой общего положения с плоскостью общего положения
Для построения точки пересечения прямой общего положения 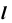
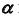
1. Заключим прямую 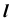
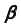
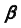
2. Строим линию пересечения заданной плоскости 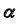
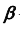
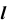
Так как линия m принадлежит заданной плоскости 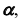
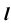
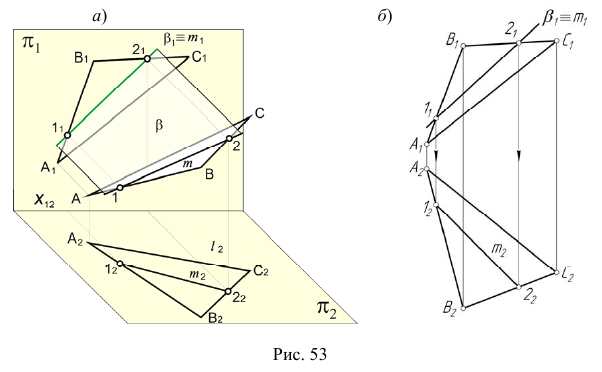
Перед решением задачи по определению точки пересечения прямой общего положения с плоскостью общего положения рассмотрим отдельно реализацию на эпюре Монжа п. 2 — построение линии пересечения проецирующей плоскости с плоскостью общего положения рис. 53, а.
Задача:
На эпюре Монжа построить проекции линии пересечения плоскости общего положения 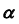
При решении этой задачи используем собирательное свойство вырожденной проекции проецирующей плоскости.
Алгоритм решения
- Определим фронтальную проекцию линии m. Так как плоскость
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
(рис. 53, б).
- Горизонтальную проекцию линии m построим, учитывая ее принадлежность плоскости
(задача 2).
- Заказать чертежи
Задача:
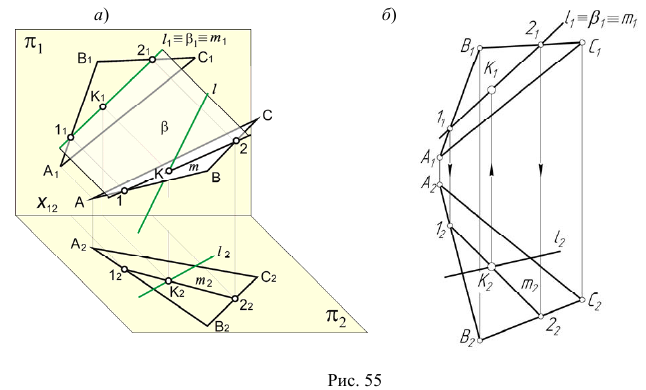
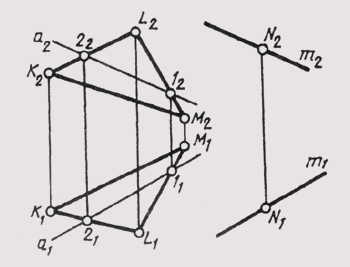
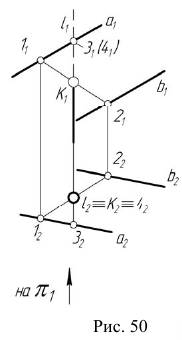
На эпюре Монжа построить проекции точки пересечения прямой общего положения l с плоскостью общего положения (ABC) (рис. 54, а).
Алгоритм решения
1. Заключим прямую линию l во вспомогательную проецирующую плоскость 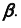
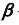
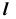
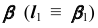
2. Построим проекции линии пересечения m заданной плоскости 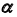
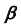
3. Определим проекции точки пересечения K прямой линии 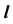
- отметим проекцию
- на пересечении
и линии проекционной связи отметим проекцию
(рис. 55, б).
4. Определим видимость прямой 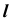
Точка K делит прямую 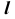
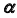
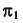
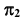
Определим видимость прямой 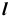
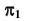
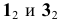
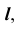
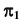
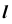
Видимость прямой 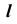
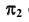
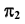
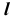
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Пересечение прямой с поверхностью
- Пересечение поверхностей
- Способы преобразования чертежа
- Ортогональное проецирование: точка, прямая, плоскость
- Отображение пространственных объектов на плоскость
- Моделирование линии на эпюре Монжа
- Моделирование плоскости на эпюре Монжа
- Моделирование поверхностей на эпюре Монжа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник

 — горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой
— горизонтально- проецирующая, то вторая проекция точки пересечения заданной прямой с плоскостью совпадает с вы- рожденной проекцией прямой  Отметим горизонтальную проекцию
Отметим горизонтальную проекцию 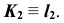
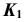 определим по принадлежности точки K плоскости
определим по принадлежности точки K плоскости 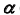 (задача 3).
(задача 3).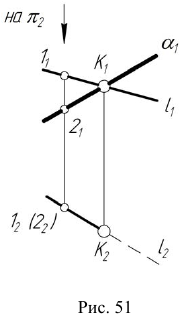
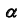 — фронтально- проецирующая, следовательно, проекция
— фронтально- проецирующая, следовательно, проекция 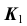 определится на пересечении фронтальных проекций прямой и плоскости
определится на пересечении фронтальных проекций прямой и плоскости 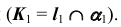
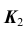 определим по принадлежности точки K прямой
определим по принадлежности точки K прямой 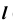 (задача 1).
(задача 1).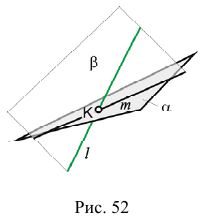
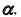
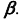
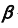 — фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости
— фронтально-проецирующая, то первая проекция линии m совпадает с вырожденной (фронтальной) проекцией плоскости 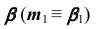 (рис. 53, б).
(рис. 53, б).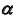 (задача 2).
(задача 2).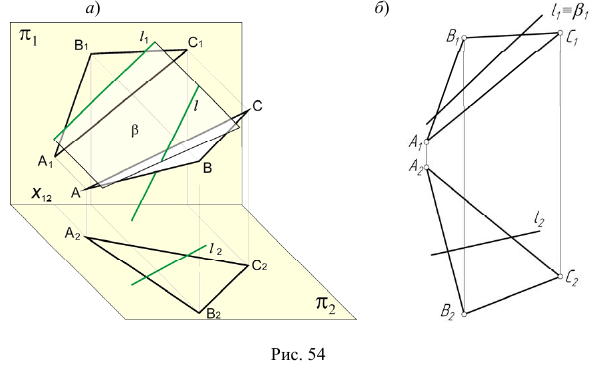
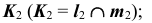
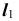 и линии проекционной связи отметим проекцию
и линии проекционной связи отметим проекцию 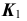 (рис. 55, б).
(рис. 55, б).