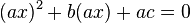Способ переброски при решении квадратных уравнений

Метод «переброски» при решении квадратных уравнений

Дата публикации: 06.04.2016 2016-04-06

Статья просмотрена: 13054 раза

Библиографическое описание:

Жигайлова, А. Б. Метод «переброски» при решении квадратных уравнений / А. Б. Жигайлова. — Текст : непосредственный // Молодой ученый. — 2016. — № 7.3 (111.3). — С. 11-13. — URL: https://moluch.ru/archive/111/27959/ (дата обращения: 20.11.2021).

На сегодняшний день перед выпускниками школ стоит главная задача – это успешная сдача итоговой аттестации, ЕНТ и поступление в ВУЗ. В числе обязательных предметов при сдаче государственного экзамена стоит математика. Математика – точная наука, она требует усердия, внимательности и сообразительности. Формулы, теоремы, доказательства и многое другое, должен знать и помнить ученик. Выучить это все не так-то просто, необходимо также уметь применять свои знания. Я выяснила, что в предложенном национальным центром тестирования пособие по предмету «математика» содержится около 25% заданий, решаемых с помощью квадратного уравнения или сводимых к нему. А это значит, что эффективное и удобное использование метода «переброски» поможет значительно сократить время при решении тестирования. Но чаще всего ученик использует формулу дискриминанта для нахождения корней квадратного уравнения. Но зачем идти трудным путем, когда есть легкое решение?! Необходимо рассмотреть метод «переброски», который позволяет решать подавляющее большинство полных квадратных уравнений устно, аналогично решению приведенных квадратных уравнений с помощью теоремы обратной теореме Виета.

Так называемый метод «переброски» позволяет сводить решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами. Он заключается в следующем:

1)умножаем обе части на выражение:

2)вводим новую переменную y=ax:

.

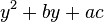
Далее уравнение решают устно описанным выше способом, затем возвращаются к исходной переменной и находят корни уравнений и .

Применение метода «переброски» при решении квадратных уравнений или уравнений сводящихся к ним.

Пример1:Решить уравнение 3х2 + 10x + 7 = 0.

Найдем дискриминант по формуле:

D = 100 – 4 * 3 * 7= 16

Найдем корни квадратного уравнения по формуле:

x1,2 = (-10 ± √16) / 2*3; x1= -7/3; x2 = -1;

Выполним «переброску» и решим это же уравнение с помощью теоремы обратной теореме Виета:

y2 + 10y + 3 · 7 = 0;

По теореме обратной теореме Виета:

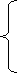
Теперь вернемся к переменной x. Для этого разделим полученные результаты y1,2 на первый коэффициент исходного уравнения, т.е. на 3. Получим:

После сокращения будем иметь x1 = -7/3; x2 = -1.

Пример 2: Решить уравнение √3×2 – 5x – √12 = 0.

По методу «переброски» будем работать не с исходным, а с новым квадратным уравнением:

у2 – 5y – √12 · √3 = 0;

Находим числа, сумма которых равна 5, а произведение равно -6.

Тогда исходное уравнение будет иметь корни:

В знаменателе уберем иррациональность. Получим:

Пример 3: Решите квадратное неравенство: 5×2 – 11x +2 › 0

Рассмотрим функцию y=5×2 – 11x +2. Графиком этой функции является парабола, ветви которой направлены вверх.

Выясним, как расположена эта парабола относительно оси x. Для этого решим уравнение 5×2 – 11x +2 =0.

Применим метод «переброски».

x1 = 10/5 =2; x2 = 1/5 = 0,2.

Значит, парабола пересекает ось х в двух точках, абсциссы которых равны 2 и 0,2.

Покажем схематически, как расположена парабола на числовой прямой

+ — +

0,2 2 x

Пример 4: Решить тригонометрическое уравнение 3sin2x – 7sinx + 4 = 0.

3sin2x – 7sinx + 4 = 0

Применим метод «переброски».

нет решения, т.к. sinxне принадлежит отрезку [-1;1]

Ответ: x= π/2 + 2πn; n ϵ z

Пример 5: Решить уравнение 4271×2 – 4272x + 1 = 0.

По рассматриваемому методу нам необходимо найти числа, сумма которых равна 4272, а произведение 4271 (после «переброски» свободный член равен 1 · 4271 = 4271). Это будут числа 4271 и 1. Тогда получим:

x1 = 4271/4271; x2 = 1/4271.

А после сокращения будем иметь корни x1 = 1; x2 = 1/4271.

Пример 6: Решить уравнение 5sin2x – 8sinxcosx + 3cos2x = 0.

Данное уравнение является однородным, разделим всё уравнение на cos2x (cos2x≠0).

5tg2x – 8tgx + 3 = 0

Заменяем tgx на tи получаем уравнение:

Применим метод «переброски»:

Найдем корни квадратного уравнения:

Следовательно,t1= 3/5; t2=5/5=1.

Вернемся к постановке

x = arctg3/5 + πn; n ϵ z.

x = π/4 + πn; n ϵ z.

Ответ: x = arctg3/5 + πn; n ϵ z,

Пример 7: Дана функция y = 2×2-3x+1. Найдите:

b) промежутки в которых y>0, y 0, ветви параболы направлены вверх, следовательно, y>0 при хϵ (-∞; 0,5)ᵁ(1; +∞),

Похожие статьи

Способы решения квадратных уравнений

Графическое решение квадратного уравнения. Решение уравнений с использованием теоремы Виета.

8. Решение квадратных уравнений с помощью номограммы.

Ответ:8,0; 1,0. 2) Решим с помощью номограммы уравнение.

Оптимальные способы решения квадратных уравнений

уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.

Метод коэффициентов при решении квадратных уравнений

Ключевые слова: уравнения, квадратные уравнения, способы решения квадратных уравнений. В школьном курсе математики изучается решение полных квадратных уравнений с помощью дискриминанта, теоремы обратной теореме Виета, выделения.

Общий вид показательных уравнений. Характеристика. Теоремы.

Характеристика. Теоремы. Показательными уравнениями называют уравнения вида:af(x)

16 ∙ =. — равенство верное. Исходному уравнению удовлетворяет только значение x = 24.

6) Получить ответ. Приведение к квадратному уравнению: 1) Записать в виде: A + B + C = 0.

Задачи и теоремы Эйлера глазами учащихся

Способ 1: выделим для решения задачи квадрат двучлена из данного квадратного трехчлена

Ответ: 1. Способ 2: извлеките кубический корень . Будем искать рациональные числа а и , такие, что .

Вычтем из второго уравнения первое, умноженное на 2, получим, что .

Решение методом продолжения задач математической физики.

Вопрос — ответ.

Для решения задач поставленных для уравнений теплопроводности в полуограниченной области мы можем использовать следующие леммы.

Разрешимость одной краевой задачи для.

Лемма 2. Для любого имеет место неравенство . (7). Определим оператор равенством и рассмотрим уравнение.

Тогда все решения задачи (3) удовлетворяют оценке. (11). где . Теорема 8. Пусть существует такое . что выполнены условия

Периодические решения разностного уравнения третьего порядка

Вопрос — ответ.

Ключевые слова: разностное уравнение третьего порядка, периодические решения, циклы, предельные циклы.

Обратная краевая задача с интегральными условиями для гиперболического уравнения второго порядка.

Об одной задаче определения правой части линейного.

Сначала с помощью функции Грина исходная прямая задача сводится к эквивалентной задаче, для которой доказывается теорема существования и

Основные термины (генерируются автоматически): обратная задача, дифференциальное уравнение, единственность решения.

Похожие статьи

Способы решения квадратных уравнений

Графическое решение квадратного уравнения. Решение уравнений с использованием теоремы Виета.

8. Решение квадратных уравнений с помощью номограммы.

Ответ:8,0; 1,0. 2) Решим с помощью номограммы уравнение.

Оптимальные способы решения квадратных уравнений

уравнение, квадратное уравнение, способ решения, свободный член, решение, корень, Древняя Индия, исходное уравнение, полный квадрат, современный вид.

Метод коэффициентов при решении квадратных уравнений

Ключевые слова: уравнения, квадратные уравнения, способы решения квадратных уравнений. В школьном курсе математики изучается решение полных квадратных уравнений с помощью дискриминанта, теоремы обратной теореме Виета, выделения.

Общий вид показательных уравнений. Характеристика. Теоремы.

Характеристика. Теоремы. Показательными уравнениями называют уравнения вида:af(x)

16 ∙ =. — равенство верное. Исходному уравнению удовлетворяет только значение x = 24.

6) Получить ответ. Приведение к квадратному уравнению: 1) Записать в виде: A + B + C = 0.

Задачи и теоремы Эйлера глазами учащихся

Способ 1: выделим для решения задачи квадрат двучлена из данного квадратного трехчлена

Ответ: 1. Способ 2: извлеките кубический корень . Будем искать рациональные числа а и , такие, что .

Вычтем из второго уравнения первое, умноженное на 2, получим, что .

Решение методом продолжения задач математической физики.

Вопрос — ответ.

Для решения задач поставленных для уравнений теплопроводности в полуограниченной области мы можем использовать следующие леммы.

Разрешимость одной краевой задачи для.

Лемма 2. Для любого имеет место неравенство . (7). Определим оператор равенством и рассмотрим уравнение.

Тогда все решения задачи (3) удовлетворяют оценке. (11). где . Теорема 8. Пусть существует такое . что выполнены условия

Периодические решения разностного уравнения третьего порядка

Вопрос — ответ.

Ключевые слова: разностное уравнение третьего порядка, периодические решения, циклы, предельные циклы.

Обратная краевая задача с интегральными условиями для гиперболического уравнения второго порядка.

Об одной задаче определения правой части линейного.

Сначала с помощью функции Грина исходная прямая задача сводится к эквивалентной задаче, для которой доказывается теорема существования и

Основные термины (генерируются автоматически): обратная задача, дифференциальное уравнение, единственность решения.

Источник

«Решение квадратных уравнений способом «переброски»
план-конспект занятия по алгебре (8 класс) на тему

Ознакомление с одним из способов решения квадратных уравнений, который можно назвать способом «переброски».

Скачать:

Вложение	Размер
sposob_perebroski.doc	93 КБ

Предварительный просмотр:

Материал к занятию по теме «Решение квадратных уравнений способом «переброски»

Тема: «Решение квадратных уравнений способом «переброски»

Тип занятия: Изучение нового материала и первичное закрепление с комплексным применением знаний и способов деятельности

Вид занятия: Урок углубления знаний

Возраст учащихся: 8 класс

Форма работы: индивидуальная, групповая

Оборудование: мультимедийный компьютер

• Познавательный
• Систематизирующий
• Коммуникативный
• Логический

Формирование знания решения квадратных уравнений с помощью способа «переброски»

• Познакомить с теорией способа решения квадратных уравнений с помощью способа «переброски»
• Познакомить с применением способа решения квадратных уравнений с помощью способа «переброски»
• Сформировать умения составлять алгоритмы для данного способа решения квадратных уравнений
• Развитие вычислительных навыков
• Развитие кругозора учащихся

• Развитие умения наблюдать, анализировать
• Способствовать интеллектуальному развитию учащихся, формированию качеств мышления, познавательных интересов, творческих способностей учащихся
• Познакомить учащихся с интересными фактами из истории
• Развитие коммуникативных качеств личности

• Воспитание навыков сотрудничества в процессе совместной работы.

• Содействовать воспитанию интереса к математике, активности, мобильности, отношения ответственной зависимости, взаимопомощи, умения общаться, толерантности у детей
• Воспитание самостоятельности, умения представлять выбранный способ решения уравнения

1. Организационный момент. Вступительное слово учителя
2. Актуализация опорных теоретических и практических знаний о квадратных уравнениях
3. Объяснение нового материала
4. Закрепление нового материала
5. Подведение итогов

Оформление доски: на доске написано

«Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением. Извне он может получить только возбуждение». А Дистервег

Вступительное слово учителя. Сообщается цель, задачи занятия, план работы на занятии.

Актуализация опорных теоретических и практических знаний.

Коллективная работа. Устно.

Прежде всего, вспомним, какие уравнения называются квадратными. /Уравнение вида , где х — переменная, a,b,c – числа , называется квадратным./ Квадратное уравнение, записанное в таком виде, является стандартным видом уравнения. Как называются числа a, b, c ?

/ а – старший коэффициент, b – второй коэффициент, с – свободный член/

Вспомним, как традиционно решаются квадратные уравнения разных видов. Первый вид квадратных уравнений – неполные квадратные уравнения. С этим видом квадратных уравнений мы познакомились на первых уроках изучения квадратных уравнений. Вспомним, какие виды неполных квадратных уравнений бывают и как они решаются.

Вспомним, как традиционно решаются квадратные уравнения, записанные в стандартном виде. Прежде всего, обратимся к понятию дискриминанта. Для чего и зачем он нужен? Вспомните слово “дискриминация”, что оно означает? Оно означает унижение одних и возвышение других, т.е. различное отношение к разным людям. Оба слова (и дискриминант, и дискриминация) происходят от одного латинского слова, означающего “различающий”. Дискриминант различает квадратные уравнения по числу корней (анализ слайда). Важное дополнение: в таких случаях ( D ) обычно уточняют – нет действительных корней. Дело в том, что в математике, кроме действительных чисел, рассматриваются так называемые мнимые числа; так вот, мнимые корни у такого уравнения есть. О мнимых числах и разрешимости таких квадратных уравнений мы поговорим в старших классах. Мы вспомнили всю “азбуку” квадратного уравнения?

/Нет. Мы не вспомнили теорему Виета./

Решение задач на применение теоремы Виета и теоремы, обратной теореме Виета.

а) В уравнениях найти подбором корни уравнения:

х 2 – 6х + 8 = 0
(Д = 1; х 1 = 2, х 2 = 4)

z 2 + 5z + 6 = 0
(Д = 1; z 1 = – 3, z 2 = –2)

б) Составить квадратное уравнение, корнями которого являются числа:

3; 4
(х 2 – 7х + 12 = 0)

–2; 5
(х 2 – 3х – 10 = 0)

в) Один из корней уравнения равен 3. Найти второй корень уравнения.

х 2 – 21х + 54 = 0
3 и ?
(х 2 = 18)

х 2 + 17х – 60 = 0
3 и ?
(х 2 = – 20)

Подведем итог этого этапа:

• Что утверждает теорема Виета?

• Сформулируйте теорему, обратную теореме Виета.

• Чему равна сумма и произведение корней квадратного уравнения ах 2 + + вх + с = 0 ?

Это интересно. Биографическая миниатюра. Ф. Виет. (Сообщение учащегося).

Формулы решения квадратных уравнений в Европе были впервые написаны в 1202 году. Вывод формулы решения квадратного уравнения встречается у французского математика Ф. Виета. Франсуа Виет родился в провинции Франции в 1540 году. Виет имел возможность получить хорошее образование и относился к обучению очень серьезно. Став юристом, он продолжал заниматься математикой, астрономией и космологией. В 1591 году Виет ввел буквенные обозначения не только для неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало впервые возможным выражение свойств уравнений и их корней формулами. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений.

По праву достойна в стихах быть воспета.
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого,
Умножишь ты корни – и дробь уж готова.
В числителе С, в знаменателе А.
А сумма корней тоже дроби равна.
Хоть с минусом дробь, что за беда?
В числителе В, в знаменателе А.

А все могло быть по-другому. Эта замечательная теорема могла быть открыта совсем другим талантливым человеком. А знаете почему?

Испанские инквизиторы изобрели очень сложную тайнопись (шифр), которая все время изменялась и дополнялась. Благодаря этому шифру воинствующая и сильная в то время Испания могла свободно переписываться с противниками французского короля даже внутри Франции, и эта переписка оставалась неразгаданной. После бесплодных попыток найти ключ к шифру король обратился к Виету. Известно, что Виет, две недели подряд дни и ночи просидев за работой, все же нашел ключ к испанскому шифру. После этого неожиданно для испанцев Франция стала выигрывать одно сражение за другим. Испанцы долго недоумевали. Наконец им стало известно, что шифр для французов уже не секрет и что виновник его расшифровки – Виет. Будучи уверенными, в невозможности разгадать способ тайнописи людьми, они обвинили Францию перед Папой Римским и инквизицией в кознях дьявола, а Виета обвинили, что он был в союзе с дьяволом и приговорили его к сожжению на костре. К счастью для науки, он не был выдан инквизиции.

Решение квадратных уравнения, используя свойства коэффициентов. (Повторение предыдущей темы факультативных занятий)

1. 345х 2 – 137х – 208 = 0
2. 313х 2 + 326х + 13 = 0

Задание учащиеся выполняют самостоятельно. Взаимоконтроль.

а + b + с = 345 – 137 – 208 = 0 , значит, х = 1 , х = – 208/345

а – b + с = 313 – 326 + 13 = 0 , значит, х = – 1 , х = – 13/313

Изучение нового материала. Ознакомление ещё с одним способом решения квадратных уравнений, который можно назвать так: способ «переброски».

Рассмотрим квадратное уравнение

ах 2 + bх + с = 0, а ≠ 0.

Умножая обе его части на а, получаем уравнение

а 2 х 2 + а bх + ас = 0.

Пусть ах = у , откуда х = ; тогда приходим к уравнению

равносильного данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета. Окончательно получаем х 1 = и х 1 = . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

• Пример 1 (объясняет учитель)

Решим уравнение 2х 2 – 11х + 15 = 0 .

Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение

у 2 – 11y + 30 = 0 .

Согласно теореме Виета

• Пример 2 (один ученик решает на доске, остальные в тетрадях)

у 1 = 6 х 1 = 6/2 х 1 = 3

у 2 = 3 ↔ х 2 = 3/2 ↔ х 2 = 1,5

«Математическая эстафета». Работа по командам. На последней парте каждого ряда находится листок с 6 заданиями (по 2 задания на каждую парту). Ученики, получившие листок, выполняют первые 2 задания (разрешается совместная работа) и передают листок впереди сидящим ребятам.

Решите уравнения, используя метод «переброски»:

1. 10х 2 – 11х + 3 = 0 3. 3х 2 + 11х + 6 = 0 5. 6х 2 + 5х – 6 = 0

1. 2х 2 + х – 10 = 0 4. 5х 2 – 11х + 6 = 0 6. 4х 2 + 12х + 5 = 0

Работа считается оконченной, когда учитель получает три листка (по количеству рядов) с выполненными 6 заданиями.

Побеждают учащиеся того ряда, в котором раньше решат шесть примеров.

Проверка итогов работы осуществляется с помощью мультимедийного компьютера.

Оценка – 6 баллов (по 1 баллу за каждый верно выполненный пример).

1. Самооценка труда учащихся:

• В каких знаниях уверен;
• Выполнил ли программу занятия полностью;
• Какие виды работ вызвали затруднения и требуют повторения;
• Помогло ли занятие продвинуться в знаниях, умениях, навыках по предмету.

2. Оценка труда товарищей:

• Насколько результативным было занятие сегодня;
• Кто, по вашему мнению, внёс наибольший вклад в его результаты;
• Кому, над чем следовало бы ещё поработать.

3. Оценка результатов занятия учителем:

• Оценка работы группы (активность, адекватность ответов, неординарность работы отдельных детей, уровень самоорганизации, прилежание).

4. Выводы по занятию.

Решить уравнения. Каждое решить 3 различными способами.

• 3х 2 + 5х – 2 = 0
• х 2 – 8х + 7 = 0
• 5х 2 – 11 х + 2 = 0

Источник