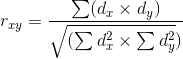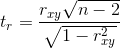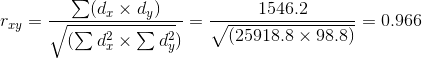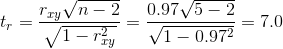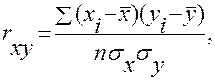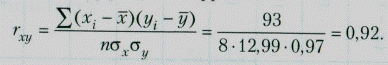Способ парной корреляции это

Библиотека постов MEDSTATISTIC об анализе медицинских данных

Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic

Критерии и методы

КРИТЕРИЙ КОРРЕЛЯЦИИ ПИРСОНА

​ – это метод параметрической статистики, позволяющий определить наличие или отсутствие линейной связи между двумя количественными показателями, а также оценить ее тесноту и статистическую значимость. Другими словами, критерий корреляции Пирсона позволяет определить, изменяется ли (возрастает или уменьшается) один показатель в ответ на изменения другого? В статистических расчетах и выводах коэффициент корреляции обычно обозначается как r_xy или R_xy.

1. История разработки критерия корреляции

Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.

2. Для чего используется критерий корреляции Пирсона?

Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.

Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.

3. Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
2. Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой — определяются при помощи регрессионного анализа.
3. Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
4. Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
5. Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.

Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.

В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.

Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов.

4. Как рассчитать коэффициента корреляции Пирсона?

Расчет коэффициента корреляции Пирсона производится по следующей формуле:

5. Как интерпретировать значение коэффициента корреляции Пирсона?

Значения коэффициента корреляции Пирсона интерпретируются исходя из его абсолютных значений. Возможные значения коэффициента корреляции варьируют от 0 до ±1. Чем больше абсолютное значение r_xy – тем выше теснота связи между двумя величинами. r_xy = 0 говорит о полном отсутствии связи. r_xy = 1 – свидетельствует о наличии абсолютной (функциональной) связи. Если значение критерия корреляции Пирсона оказалось больше 1 или меньше -1 – в расчетах допущена ошибка.

Для оценки тесноты, или силы, корреляционной связи обычно используют общепринятые критерии, согласно которым абсолютные значения r_xy 0.7 — о сильной связи.

Более точную оценку силы корреляционной связи можно получить, если воспользоваться таблицей Чеддока:

Абсолютное значение rxy	Теснота (сила) корреляционной связи
менее 0.3	слабая
от 0.3 до 0.5	умеренная
от 0.5 до 0.7	заметная
от 0.7 до 0.9	высокая
более 0.9	весьма высокая

Оценка статистической значимости коэффициента корреляции r_xy осуществляется при помощи t-критерия, рассчитываемого по следующей формуле:

Полученное значение t_r сравнивается с критическим значением при определенном уровне значимости и числе степеней свободы n-2. Если t_r превышает t_крит, то делается вывод о статистической значимости выявленной корреляционной связи.

6. Пример расчета коэффициента корреляции Пирсона

Целью исследования явилось выявление, определение тесноты и статистической значимости корреляционной связи между двумя количественными показателями: уровнем тестостерона в крови (X) и процентом мышечной массы в теле (Y). Исходные данные для выборки, состоящей из 5 исследуемых (n = 5), сведены в таблице:

N	Содержание тестостерона в крови, нг/дл (X)	Процент мышечной массы, % (Y)
1.	951	83
2.	874	76
3.	957	84
4.	1084	89
5.	903	79

Вычислим суммы анализируемых значений X и Y:

Σ(X) = 951 + 874 + 957 + 1084 + 903 = 4769

Σ(Y) = 83 + 76 + 84 + 89 + 79 = 441

Найдем средние арифметические для X и Y:

M_x = Σ(X) / n = 4769 / 5 = 953.8

M_y = Σ(Y) / n = 441 / 5 = 82.2

Рассчитаем для каждого значения сопоставляемых показателей величину отклонения от среднего арифметического d_x = X — M_x и d_y = Y — M_y:

N	Содержание тестостерона в крови, нг/дл (X)	Процент мышечной массы, % (Y)	Отклонение содержания тестостерона от среднего значения (dx)	Отклонение % мышечной массы от среднего значения (dy)
1.	951	83	-2.8	0.8
2.	874	76	-79.8	-6.2
3.	957	84	3.2	1.8
4.	1084	89	130.2	6.8
5.	903	79	-50.8	-3.2

Возведем в квадрат каждое значение отклонения d_x и d_y:

N	Содержание тестостерона в крови, нг/дл (X)	Процент мышечной массы, % (Y)	Отклонение содержания тестостерона от среднего значения (dx)	Отклонение % мышечной массы от среднего значения (dy)	dx 2	dy 2
1.	951	83	-2.8	0.8	7.84	0.64
2.	874	76	-79.8	-6.2	6368.04	38.44
3.	957	84	3.2	1.8	10.24	3.24
4.	1084	89	130.2	6.8	16952,04	46.24
5.	903	79	-50.8	-3.2	2580,64	10.24

Рассчитаем для каждой пары анализируемых значений произведение отклонений d_x x d_y:

N	Содержание тестостерона в крови, нг/дл (X)	Процент мышечной массы, % (Y)	Отклонение содержания тестостерона от среднего значения (dx)	Отклонение % мышечной массы от среднего значения (dy)	dx 2	dy 2	dx x dy
1.	951	83	-2.8	0.8	7.84	0.64	-2.24
2.	874	76	-79.8	-6.2	6368.04	38.44	494.76
3.	957	84	3.2	1.8	10.24	3.24	5.76
4.	1084	89	130.2	6.8	16952,04	46.24	885.36
5.	903	79	-50.8	-3.2	2580,64	10.24	162.56

Определим значения суммы квадратов отклонений Σ(d_x 2 ) и Σ(d_y 2 ):

Найдем значение суммы произведений отклонений Σ(d_x x d_y):

Рассчитаем значение коэффициента корреляции Пирсона r_xy по приведенной выше формуле:

Найдем значение t-критерия для оценки статистической значимости корреляционной связи:

Критическое значение t-критерия найдем по таблице, где при числе степеней свободы f = n-2 = 3 и уровне значимости p = 0.01 значение t_крит = 5.84. Рассчитанное значение t_r (7.0) больше t_крит (5.84), следовательно связь является статистически значимой.

Сделаем статистический вывод:

Источник

Парная корреляция

Парная корреляция позволяет оценить тесноту связи между двумя признаками. Для выявления корреляционной связи между двумя признаками можно построить поле корреляции.

Поле корреляции — это поле точек, координаты которых (х; у) определяются значениями факторного и результативного признаков.

Расположение точек на поле корреляции позволяет судить о наличии и о характере связи (нелинейная, а если линейная, то и о направлении (прямая или обратная)).

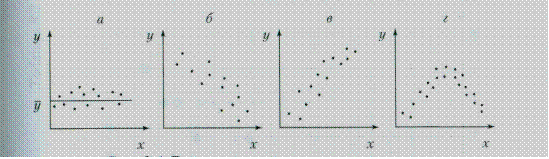
На рис. 1.1 показаны основные возможные способы расположения точек поля корреляции. Если точки поля корреляции располагаются в определенном направлении, то можно предположить наличие связи.

Рис. 1.1. Возможное расположение точек поля корреляции (х; у):

а – корреляция отсутствует; б – корреляция линейная обратная;

в – корреляция линейная прямая; г — корреляция нелинейная.

Пример 1.1. Изучается зависимость оценки, полученной на экзамене (у) 8 студентами, от суммы баллов (х), набранных ими в течение семестра. Данные приведены в табл. 1.1.

Номер студента

Оценка на экзамене (у)

Сумма баллов (х)

Для построения поля корреляции в координатных осях:

— на оси Х отложим значения баллов х, набранных студентами в течение семестра;

— на оси У покажем значения оценки у, полученной на экзамене студентами;

— нанесем точки с координатами (х; у) для каждого студента.

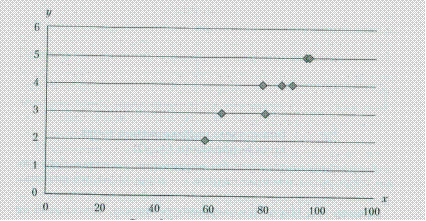
На рис. 1.2 показано поле корреляции. Расположение точек позволяет предположить, что существует прямая линейная связь между оценкой, полученной на экзамене (у) студентами, и суммой баллов (х), полученных ими в течение семестра.

Рис. 1.2. Поле корреляции

Теснота линейной связи измеряется коэффициентом парной корреляции:

где — число наблюдений; — среднее квадратическое отклонение фактора х; — среднее квадратическое отклонение результата у. Или .

Если знаки отклонений от средних совпадают, то связь прямая ,

если знаки отклонений не совпадают, то связь обратная .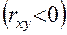

Величина коэффициента парной корреляции изменяется от -1 (полная обратная связь) до 1 (полная прямая связь):

.

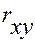
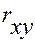
Чем ближе значение к единице, тем связь теснее, чем ближе значение к нулю, тем она слабее.

Коэффициент корреляции — это симметричная мера связи, т.е. это мера взаимосвязи между х и у. Поэтому .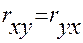

Характеризовать тесноту связи поможет следующая таблица:

Коэффициент корреляции	Характеристика связи
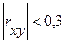	Слабая
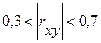	Средняя
	Сильная или тесная

По данным примера табл. 1.1 рассчитаем коэффициент парной корреляции между оценкой (у), полученной на экзамене студентами, и суммой баллов (х), полученных ими в течение семестра:

— вычислим средние значения признаков:

— вычислим средние квадратические отклонения признаков и ,

данные для расчета которых приведены в табл. 1.2:

— вычислим коэффициент корреляции:

Полученное значение 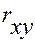близко к единице, что свидетельствует о тесной связи между результатом и фактором.

Величина называется коэффициентом детерминации и показывает долю вариации результативного признака под действием факторного признака. Коэффициент детерминации может быть выражен в процентах. Коэффициент детерминации принимает значения в интервале [0; 1]. Чем ближе значение к единице, тем больше вариация результативного признака обусловлена вариацией факторного признака, и наоборот.

Для нашего примера = 0,85, т.е. сумма накопленных баллов течение семестра объясняет 85% различий в оценках, получаемых на экзамене.

Источник

Читайте также:  Нормакс таблетки способ применения