Способ оценки влияния факторов способ цепных подстановок

Метод цепных подстановок

Способ цепных подстановок может быть использован во всех типах детерминированных факторных моделей (аддитивные, мультипликативные, кратные, комбинированные) для расчёта величины влияния фактора на результат.

Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде. С этой целью рассчитывают ряд условных величин, которые учитывают изменение одного, двух и т.д. факторов, допуская, что остальные факторы не меняются. Сравнение величины результата до и после изменения уровня того или иного фактора позволяют элиминироваться от влияний всех факторов, кроме одного.

Алгоритм метода цепных подстановок для многофакторной мультипликативной модели

1. Рассчитываем плановый показатель: Y0 = a0 * b0 * с0* d0;

2. Далее рассчитывается система условных показателей:
Y_усл.1 = a1 * b0 * с0* d0;
Y_усл.2 = a1 * b1 * с0* d0;
Y_усл.3 = a1 * b1 * с1* d0;

3. Рассчитываем фактический показатель: Y1 = a1 * b1 * с1* d1;

4. Путем последовательного вычитания полученных показателей находим изменение результативного показателя за счет факторов:
ΔYа = Y_усл.1 – Y0;
ΔYb = Y_усл.2 – Y_усл.1;
ΔYс = Y_усл.3 – Y_усл.2;
ΔYd = Y1– Y_усл.3;
5. Рассчитываем общее отклонение фактического показателя от планового, которое равно сумме факторных отклонений:
ΔY = Y1 — Y0 = ΔYа + ΔYb + ΔYс + ΔYd

Рекомендации при использовании этого метода:
А) в первую очередь учитываются изменения количественных показателей, затем качественные;
Б) сначала учитываются факторы первого уровня подчинения, затем второго и т.д.

Пример . Исходные данные для расчета влияния факторов базисные: (y0 = 1,58; a0 = 12940; b0 = 8210 ) и фактические: (y1 = 1,53; a1 = 13950; b1 = 9124; ). Рассчитайте влияние на отклонение результативного показателя (y) каждого из определяющих его факторов (a, b).

Источник

Способ (метод) цепных подстановок. Понятие, примеры использования, алгоритм расчета

Сегодня на жизнь каждого человека или отдельной организации оказывает воздействие масса факторов, начиная от политики и заканчивая «соседом» или внутренними возможностями. Чтобы определить, какой из параметров оказывает наиболее существенное влияние, необходимо провести тотальный анализ внешней и внутренней среды, оценить степень «могущества» фактора и принять решение о конкретных действиях по его смягчению.

Сегодня на жизнь каждого человека или отдельной организации оказывает воздействие масса факторов, начиная от политики и заканчивая «соседом» или внутренними возможностями. Чтобы определить, какой из параметров оказывает наиболее существенное влияние, необходимо провести тотальный анализ внешней и внутренней среды, оценить степень «могущества» фактора и принять решение о конкретных действиях по его смягчению.

Студенты экономического факультета изучают различные методики анализа финансово-хозяйственной деятельности компании, в том числе и те методы, позволяющие определить «авторитетные» параметры, воздействующие на работу фирмы. К такой методике относят метод цепных подстановок.

Что это такое?

Метод цепных подстановок – это особый способ, позволяющий определить, какой из конкретных параметров оказывает существенное влияние на работу индивида или компании в целом. Он считается одним из простейших вариантов установления взаимосвязей и воздействующих факторов. Для его реализации не требуется колоссальных знаний и умений, достаточно следовать определенному алгоритму и выполнять простейшие математические операции: сложение, вычитание, умножение и деление.

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

В основе метода цепных подстановок лежит детерминация, то есть принцип определения: какой вклад сделал каждый элемент одной системы? Судя по «доле вложений», определяется степень его влияния на объект в целом.

Достоинства и недостатки методики

К преимуществам способа цепных подстановок относят:

• Универсальность: он применим к любой системе (простой и сложной). Алгоритм действий стандартен и ничем не отличается;
• Простота расчетов: достаточно грамотно и правильно пользоваться математическими операциями, чтобы определить эффект воздействия каждого фактора;
• Позволяет установить взаимосвязь разных критериев и определить, как они воздействуют на результат;
• Здесь не учитываются какие-либо нормативы, нет ограничений в зависимости от исследуемого фактора, что упрощает анализ динамики;
• Минимум затрачиваемого времени на расчеты и выводы. Все становится очевидным уже после проведения 50% анализа.

Плюсы метода цепных установок

К недостаткам метода относят:

• Перемена мест слагаемых может исказить результат, поэтому важно придерживаться строго той «формулы расчета», которая была утверждена изначально;
• Определение степени влияния фактора производится с некой погрешностью, что может поставить результаты анализа под сомнение.

Как работает метод цепных подстановок?

Действие этого принципа предполагает, что исследователь будет придерживаться конкретных правил:

• вычисление «авторитетности» каждого критерия производится последовательно (то есть сначала оценивается изменение первого параметра, затем второго и пр.);
• важно помнить, что замена изучаемых критериев производится либо с планового на фактический, либо с базисного (прошлогодний показатель) на текущий.
• Необходимо ввести систему обозначений (она может быть произвольной главное чтоб автор понимал, что есть что): например, Апл. – плановый показатель А, Аф. – фактический показатель А или А18 – показатель за 2018 год, А19 — показатель за 2019 год и т.д.
• Запомните, плановые показатели – всегда более ранние сведения, а фактические — более свежие.

Анализ воздействия каждого фактора происходит путем постепенной замены данных. Рассмотрим работу метода на следующем примере:

Применение метода на конкретном примере

Соблюдение последнего условия обязательно. Фактически оно удостоверяет, что аналитик выполнил все расчеты и замены верно.

Метод цепных подстановок успешно применяются экономистами и аналитиками в целях оптимизации производства, корректировки производственной или финансовой политики, создания более выгодных условий производства и реализации. Он позволяет оценить любую сторону компании, выявить наиболее влиятельный параметр в любом сегменте.

Студенты экономических факультетов ВУЗов изучают его. Для разработки и тренировки применения методики они решают различные задачи (пример ниже).

Изучение метода студентам-экономистами

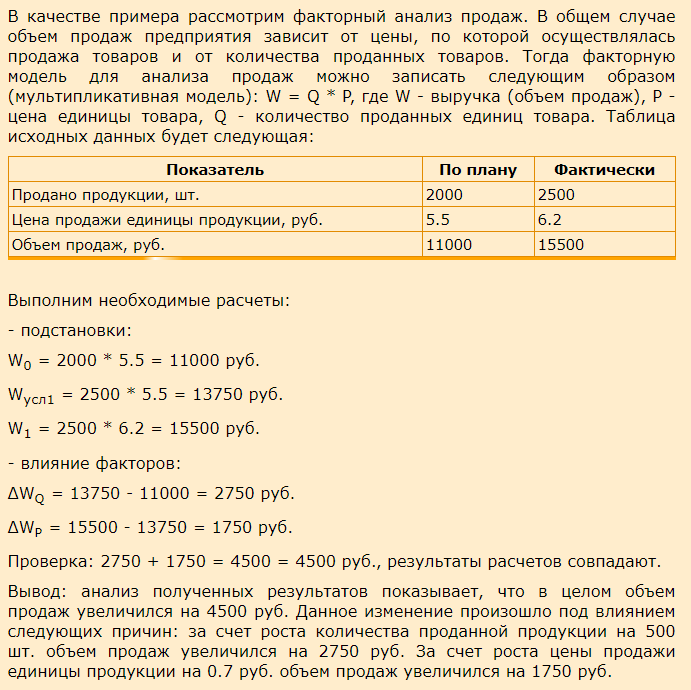
Чтобы убедиться в правильности расчетов, необходимо изначально сохранять внимательность, перепроверить каждое действие и использовать общепринятые формулы. Метод цепных подстановок позволяет наглядно показать, какой из критериев в какую сторону изменил жизнь объекта, как все изучаемые показатели взаимосвязаны и действуют в одной целой системе.

Таким образом, основой действия данного способа является последовательность замены параметров и определение степени влияния каждого из них. Достаточно выполнить простейшие математические операции, чтобы разобраться в ситуации и скорректировать поведение, смягчить воздействие «авторитетного» критерия.

В настоящее время существуют онлайн-калькуляторы, которые произведут все необходимые расчеты за Вас, но знать суть способа обязан каждый уважающий себя квалифицированный специалист.

Трудности с учебой?

Помощь в написании студенческих и
аспирантских работ!

Источник

Способ цепных подстановок детерминированного факторного анализа

Построив факторную модель детерминированного анализа, необходимо определить способ оценки влияния факторов. В детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Наиболее универсальным способом является способ цепных подстановок, который используется для расчета влияния факторов во всех типах детерминированных факторных моделей – аддитивных, мультипликативных, кратных, смешанных.

Способ цепных подстановок используется для того, чтобы выявить, какие факторы влияли на анализируемый показатель и из всех действующих факторов выделить основные, имеющие решающее влияние на изменение показателя.

Сущность способа заключается в том, чтобы, определяя действие одного фактора, другие факторы принимать как неизменные. Для этого в расчетах последовательно заменяют частные плановые (базовые) показатели отчетными (фактическими). Полученные результаты сравнивают с имеющимися предыдущими данными. Разность показывает размер влияния данного фактора на изменение совокупного показателя.

Данный способ основан на элиминировании. Элиминировать – значит устранить, исключить воздействие всех факторов на величину результативного показателя, кроме одного. При этом, исходя из того, что все факторы изменяются независимо друг от друга, сначала изменяют один фактор, а все остальные оставляют без изменения. Потом изменяют два фактора при неизменности остальных и т.д.

В общем виде применение способа цепных постановок можно описать следующим образом:

y0 = a0 * b0 * c0;
ya = a1 * b0 * c0;
yb = a1 * b1* c0;
y1 = a1 * b1 * c1;
где a0, b0, c0 — базисные значения факторов, оказывающих влияние на обобщающий показатель у; a1 , b1, c1 — фактические значения факторов; ya, yb, — промежуточные (условные) изменения результирующего показателя, связанного с изменением факторов а, b, соответственно.

Общее изменение Δу = у1 – у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора при фиксированных значениях остальных факторов:

Δy = Δya + Δyb + Δyc; Δya = ya – y0; Δyb = yb – ya; Δyc = y1 – yb.

Пример применения способа цепных подстановок

Порядок применения способа цепных подстановок рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников и их выработки способом цепных подстановок. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Изменение (+,-)
				Абсолютное	Относительное, %
Объем валовой продукции, тыс. руб.	ВП	2920	3400	+480	16,40
Среднесписочная численность персонала, чел.	ЧР	20	25	+5	25,00
Среднегодовая выработка продукции одним работником, тыс. руб.	ГВ	146	136	-10	-6,85

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью двухфакторной мультипликативной модели: ВП = ЧР * ГВ.

Алгоритм расчета способом цепной подстановки таков:

• ВП0 = ЧР0 * ГВ0 = 20 *146 = 2920 тыс. руб.
  Тогда влияние изменения численности персонала на обобщающий показатель можно рассчитать по формуле:
  ВПусл1 = ЧР1 * ГВ0 = 25 *146 = 3650 тыс. руб.,
  ΔВПусл1 = ВПусл1 — ВП0 = 3650 — 2920 = 730 тыс. руб.
• Далее определим влияние изменения выработки продукции одним работником на обобщающий показатель:
  ВП1 = ЧР1 * ГВ1 = 25 *136 = 3400 тыс. руб.,
  ΔВПусл2 = ВП1 — ВПусл1 = 3400 — 3650 = — 250 тыс. руб.
• Суммарное влияние двух факторов определим по формуле:
  ΔВП = ΔВПусл1+ ΔВПусл2 = 730 + (-250) = 480 тыс. руб. — значение совпадает с табличным и подтверждает правильность расчетов.

Вывод. Таким образом, на изменение объема производства продукции положительное влияние оказало увеличение на 5 человек численности персонала, что вызвало увеличение объема производства на 730 тыс. руб., и отрицательное влияние оказало снижение выработки на 10 тыс. руб., что вызвало снижение объема на 250 тыс. руб. Суммарное влияние двух факторов привело к увеличению объема производства на 480 тыс. руб.

Необходимо отметить, что не смотря на универсальность применения и простоту расчетов способ цепных подстановок имеет следующий недостаток: в зависимости от выбранного порядка замены факторов, результаты факторного разложения имеют разные значения.

На практике точностью оценки факторов пренебрегают, выдвигая на первый план относительную значимость влияния того или иного фактора. Однако существуют правила, определяющие последовательность подстановки:

• при наличии в факторной модели количественных и качественных показателей в первую очередь рассматривается влияние количественных факторов;
• если модель представлена несколькими количественными и качественными показателями, то сначала рассматривается влияние факторов первого уровня подчинения, а затем более низкого.

Источник

Способ оценки влияния факторов способ цепных подстановок

нЕФПД МАВПК ОБХЛЙ ПУОПЧЩЧБЕФУС ОБ ЕДЙОПН НЕФПДЕ ДЙБМЕЛФЙЮЕУЛПЗП РПЪОБОЙС РТЕДНЕФБ. ьФП ПЪОБЮБЕФ, ЮФП Й ЬЛПОПНЙЮЕУЛЙК БОБМЙЪ ПУОПЧЩЧБЕФУС ОБ ДЙБМЕЛФЙЛЕ Й ЙЪХЮБЕФ ИПЪСКУФЧЕООХА ДЕСФЕМШОПУФШ РТЕДРТЙСФЙК Ч ДЙОБНЙЛЕ РХФЕН УТБЧОЕОЙС РПЛБЪБФЕМЕК Ч РТПУФТБОУФЧЕ Й ЧТЕНЕОЙ: ДЕСФЕМШОПУФШ ПДОПЗП РТЕДРТЙСФЙС УТБЧОЙЧБЕФУС У ДЕСФЕМШОПУФША ДТХЗЙИ Й УТБЧОЕОЙЕ ДЕМБЕФУС РП ЗПДБН. чУЕ ИПЪСКУФЧЕООЩЕ РТПГЕУУЩ ЙЪХЮБАФУС ЧП ЧЪБЙНПУЧСЪЙ, ЮФП ПУПВЕООП ИБТБЛФЕТОП ДМС ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ, ЛПФПТЩК ПУОПЧЩЧБЕФУС ОБ ЙЪХЮЕОЙЙ ЖБЛФПТПЧ, ЧМЙСАЭЙИ ОБ РПЛБЪБФЕМЙ. йНЕООП РПЬФПНХ ЬЛПОПНЙЮЕУЛЙК БОБМЙЪ ДБЕФ ПВЯЕЛФЙЧОХА ПГЕОЛХ ЙФПЗПЧ ДЕСФЕМШОПУФЙ РТЕДРТЙСФЙС. йНЕООП ЬЛПОПНЙЮЕУЛЙК БОБМЙЪ, ЙУРПМШЪХЕФ ТБЪТБВПФЛЙ ЛПНРМЕЛУОПЗП РПДИПДБ Л ЙЪХЮЕОЙА ДЕСФЕМШОПУФЙ РТЕДРТЙСФЙС. ч ЛПНРМЕЛУОПН БОБМЙЪЕ ЧУЕ РПЛБЪБФЕМЙ-ЖБЛФПТЩ ТБУУНБФТЙЧБАФУС ЧП ЧЪБЙНПУЧСЪЙ Й ДЕМБАФ БОБМЙЪ РЕТУРЕЛФЙЧОЩН ОБРТБЧМЕОЙЕН ЬЛПОПНЙЮЕУЛЙИ ЙУУМЕДПЧБОЙК.

ч УЧСЪЙ У ФЕН, ЮФП ЬЛПОПНЙЮЕУЛЙК БОБМЙЪ ПФОПУЙФУС Л НПМПДЩН ОБХЛБН, ЬЛПОПНЙУФЩ ЕЭЕ ОЕ ПРТЕДЕМЙМЙ ЕДЙОПК ИБТБЛФЕТЙУФЙЛЙ НЕФПДБ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ ЛБЛ ОБХЛЙ. рП ПРТЕДЕМЕОЙА вБЛБОПЧБ н.й. Й ыЕТЕНЕФБ б.д.: «РПД НЕФПДПН ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ РПОЙНБЕФУС ДЙБМЕЛФЙЮЕУЛЙК УРПУПВ РПДИПДБ Л ЙЪХЮЕОЙА ИПЪСКУФЧЕООЩИ РТПГЕУУПЧ Ч ЙИ УФБОПЧМЕОЙЙ Й ТБЪЧЙФЙЙ». рП НОЕОЙА НОПЗЙИ ЬЛПОПНЙУФПЧ ЬФП ПРТЕДЕМЕОЙЕ ОЕРПМОПЕ Й ЕЗП ОЕПВИПДЙНП ДПРПМОЙФШ ЙУРПМШЪПЧБОЙЕН УРЕГЙБМШОЩИ РТЙЕНПЧ ДМС ПВТБВПФЛЙ РПЛБЪБФЕМЕК РМБОБ ХЮЕФБ, ПФЮЕФОПУФЙ.

рП ПРТЕДЕМЕОЙА УРЕГЙБМЙУФПЧ ВЕЪ УТБЧОЕОЙС ОЕФ БОБМЙЪБ, Ф.Л. ТБУЛМБДЩЧБС ПВЯЕЛФ ОБ УПУФБЧОЩЕ ЬМЕНЕОФЩ, ЬЛПОПНЙУФЩ РТПЧПДСФ УТБЧОЕОЙЕ ЙЪНЕОЕОЙК Ч ОЙИ ЛБЛ ЧП ЧТЕНЕОЙ, ФБЛ Й РТПУФТБОУФЧЕ. еУМЙ ПВЯЕЛФПН ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ СЧМСЕФУС РТЙВЩМШ, ФП ЕЕ ОЕПВИПДЙНП ЙЪХЮЙФШ РП РЕТЙПДБН ЧТЕНЕОЙ — ЛЧБТФБМБН, ЗПДБН; Ч РТПУФТБОУФЧЕ — РП РТЕДРТЙСФЙСН, ЧЙДБН ДЕСФЕМШОПУФЙ Й Ф.Д., РП УПУФБЧОЩН ЬМЕНЕОФБН — ЧЩТХЮЛБ ПФ ТЕБМЙЪБГЙЙ, УЕВЕУФПЙНПУФШ Й Ф.Д. оП ЙЪХЮЕОЙЕ ОЕ ДБЕФ ТЕЪХМШФБФПЧ ЕУМЙ ОЕ ЙУРПМШЪПЧБФШ РТЙЕН УТБЧОЕОЙС.

чУЕ ИПЪСКУФЧЕООЩЕ РТПГЕУУЩ ЙЪХЮБАФУС РП ЪБЛПОБН ДЙОБНЙЛЙ ЧП ЧЪБЙНПУЧСЪЙ, ЮФП ПУПВЕООП ИБТБЛФЕТОП ДМС ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ, Ф.Л. ПО ЙЪХЮБЕФ УПУФБЧОЩЕ ЬМЕНЕОФЩ (ЖБЛФПТЩ) РТПГЕУУПЧ, РПЛБЪБФЕМЕК, ПФДЕМСЕФ ОЕЗБФЙЧОЩЕ Й РПЪЙФЙЧОЩЕ, ЬЛУФЕОУЙЧОЩЕ Й ЙОФЕОУЙЧОЩЕ Й ПВПВЭБЕФ ПГЕОЛХ ЙФПЗПЧ ДЕСФЕМШОПУФЙ ИПЪСКУФЧХАЭЙИ ПВЯЕЛФПЧ.

фБЛЙН ПВТБЪПН Ч НЕФПДЕ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ РТПСЧМСАФУС ПУПВЕООПУФЙ ЕЗП ЧЙДПЧ, РТЙЕНПЧ ЙУУМЕДПЧБОЙС. фБЛ, ЛПНРМЕЛУОЩК ЙМЙ УЙУФЕНОЩК РПДИПД ПРТЕДЕМСЕФ ЧЪБЙНОХА ХЧСЪЛХ ЖБЛФПТПЧ Й ЙУУМЕДПЧБОЙЕ ПВЯЕЛФПЧ ЧП ЧЪБЙНПУЧСЪЙ, ДБЕФ ЧПЪНПЦОПУФШ РТПЗОПЪЙТПЧБФШ РПЛБЪБФЕМЙ, ОБЙВПМЕЕ ПВЯЕЛФЙЧОП ПГЕОЙЧБФШ ТЕЪХМШФБФЩ.

нЕФПД ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ ЛБЛ Й ДТХЗПК ОБХЛЙ ТБУЛТЩЧБЕФУС Й ДЕКУФЧХЕФ ЮЕТЕЪ УЙУФЕНХ РТЙЕНПЧ Й УРПУПВПЧ, У РПНПЭША ЛПФПТЩИ ЙУУМЕДХАФУС ПВЯЕЛФЩ БОБМЙЪБ.

ч ЬЛПОПНЙЮЕУЛПК МЙФЕТБФХТЕ ЙИ РТЙОСФП ДЕМЙФШ РП ДЧХН ОБРТБЧМЕОЙСН: ФТБДЙГЙПООЩЕ Й ЬЛПОПНЙЛП-НБФЕНБФЙЮЕУЛЙЕ.

оБЙВПМЕЕ РПРХМСТОЩНЙ СЧМСАФУС, ЮБУФП РТЙНЕОСЕНЩЕ Ч ФЕПТЙЙ Й Ч РТБЛФЙЛЕ Й РПФПНХ ОБЪЧБООЩЕ ФТБДЙГЙПООЩНЙ — РТЙЕНЩ БВУПМАФОЩИ, ПФОПУЙФЕМШОЩИ Й УТЕДОЙИ ЧЕМЙЮЙО, ЗТХРРЙТПЧПЛ, ЬМЙНЙОЙТПЧБОЙС, ВБМБОУПЧПК ХЧСЪЛЙ, РТПГЕОФОЩИ Й БВУПМАФОЩИ ТБЪОЙГ, ГЕРОЩИ РПДУФБОПЧПЛ Й Ф.Д.

ч ЛХТУЕ «пВЭБС ФЕПТЙС УФБФЙУФЙЛЙ» РПДТПВОП ДБОЩ РТЙЕНЩ БВУПМАФОЩИ, ПФОПУЙФЕМШОЩИ Й УТЕДОЙИ ЧЕМЙЮЙО, ЗТХРРЙТПЧПЛ.

рТЙЕН ЬМЙНЙОЙТПЧБОЙС ЫЙТПЛП РТЙНЕОСЕФУС Ч ЖБЛФПТОПН БОБМЙЪЕ Й РТЕДРПМБЗБЕФ ЙУЛМАЮЕОЙЕ ЧМЙСОЙС ЧУЕИ ЖБЛФПТПЧ, ЪБ ЙУЛМАЮЕОЙЕН БОБМЙЪЙТХЕНПЗП. ьФПФ РТЙЕН ПУОПЧБО ОБ ЛПТТЕЛФЙТПЧЛЕ, Ф.Е. ЪБНЕОЕ РМБОПЧПЗП ЙМЙ ВБЪЙУОПЗП ЪОБЮЕОЙС ОБ ЕЗП ЖБЛФЙЮЕУЛПЕ ЙМЙ ПФЮЕФОПЕ ЪОБЮЕОЙЕ, РПЬФПНХ Ч ПФДЕМШОЩИ ТБУЮЕФБИ ПО ОБЪЧБО РТЙЕНПН ЛПТТЕЛФЙТПЧЛЙ.

ыЙТПЛПЕ ТБУРТПУФТБОЕОЙЕ ЛПНРШАФЕТОПК ФЕИОЙЛЙ РПЪЧПМЙМП БЛФЙЧОЕЕ РТЙНЕОСФШ Ч ФЕПТЙЙ Й РТБЛФЙЛЕ ЬЛПОПНЙЛП-НБФЕНБФЙЮЕУЛЙЕ НЕФПДЩ (ьнн) Ч БОБМЙФЙЮЕУЛЙИ ЙУУМЕДПЧБОЙСИ. ч ЪБЧЙУЙНПУФЙ ПФ ГЕМЕК Й ЪБДБЮ БОБМЙЪБ, ЧПЪНПЦОПУФЙ РПДВПТБ ЙОЖПТНБГЙЙ, ЕЈ УЙУФЕНБФЙЪБГЙЙ Й РПДЗПФПЧЛЙ Л БОБМЙЪХ ЪБЧЙУЙФ Й ЧЩВПТ НЕФПДБ.

оБЙВПМЕЕ ЮБУФП РТЙНЕОСАФУС РТЙЕНЩ ЧБТЙБГЙЙ (ЛПМЕВМЕНПУФЙ) ЙМЙ ДЙУРЕТУЙЙ, ЛПТТЕМСГЙЙ, ТЕЗТЕУУЙЙ Й ДТ. йИ ЙУРПМШЪПЧБОЙЕ ЧПЪНПЦОП, ЕУМЙ УПВМАДБЕФУС ТСД ХУМПЧЙК:

• ПВЯЕН ЧЩВПТЛЙ ДПУФБФПЮОЩК(ВПМЕЕ 20-25);
• Ч ЧЩВПТЛЕ ДБООЩИ РТПСЧМСЕФУС ЮЕФЛБС ЪБЛПОПНЕТОПУФШ (ФЕОДЕОГЙС) ТБЪЧЙФЙС;
• ЪБЧЙУЙНПУФШ ТЕЪХМШФБФЙЧОПЗП РПЛБЪБФЕМС ПФ ЖБЛФПТБ(ПЧ) ДПУФБФПЮОП ЧЩУПЛБ.

чБЦОЩН ХУМПЧЙЕН ПРФЙНБМШОПЗП РПДВПТБ РТЙЕНПЧ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ СЧМСЕФУС ЗТХРРЙТПЧЛБ ЖБЛФПТПЧ Й РПЛБЪБФЕМЕК. чБЦОП ПРТЕДЕМЙФШ, ЛБЛПК ЙЪ РПЛБЪБФЕМЕК ЧЩРПМОСЕФ ТПМШ ЖБЛФПТОПЗП, Б ЛБЛПК ТЕЪХМШФБФЙЧОПЗП. ьФБ ТПМШ ВХДЕФ ЪБЧЙУЕФШ ПФ УПДЕТЦБОЙС БМЗПТЙФНБ ТБУЮЕФБ ТЕЪХМШФБФЙЧОПЗП РПЛБЪБФЕМЕК Й ХЧСЪЛЙ Ч ОЕН ЖБЛФПТПЧ. уПДЕТЦБОЙЕ ЖБЛФПТПЧ РП ЙИ ТПМЙ НПЦЕФ ВЩФШ ЛБЮЕУФЧЕООЩН — ЙОФЕОУЙЧОЩН ЙМЙ ЛПМЙЮЕУФЧЕООЩН — ЬЛУФЕОУЙЧОЩН.

йУРПМШЪПЧБОЙЕ НЕФПДБ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ РТЕДХУНБФТЙЧБЕФ УПРПУФБЧЙНПУФШ РПЛБЪБФЕМЕК ЧП ЧТЕНЕОЙ Й Ч РТПУФТБОУФЧЕ, ЮФП Ч УПЧТЕНЕООЩИ ХУМПЧЙСИ СЧМСЕФУС ПДОПК ЙЪ УМПЦОЩИ РТПВМЕН (ТБУУНБФТЙЧБЕФУС Ч ФЕНЕ 6).

уХЭОПУФШ РТЙЕНБ ЛПТТЕЛФЙТПЧПЛ ЪБЛМАЮБЕФУС Ч ФПН, ЮФП ЧНЕУФП ЪОБЮЕОЙС ВБЪЙУОПЗП, ОПТНБФЙЧОПЗП ЙМЙ РМБОПЧПЗП ЖБЛФПТБ РПДУФБЧМСЕФУС ЪОБЮЕОЙЕ ЖБЛФЙЮЕУЛПЗП. рПМХЮЕООЩК УЛПТТЕЛФЙТПЧБООЩК РПЛБЪБФЕМШ УПРПУФБЧМСЕФУС ЪБФЕН Ч ТБЪМЙЮОЩИ ЧБТЙБГЙСИ У ВБЪЙУОЩН, РМБОПЧЩН, ОПТНБФЙЧОЩН, ДТХЗЙН УЛПТТЕЛФЙТПЧБООЩН ЙМЙ ЖБЛФЙЮЕУЛЙН РПЛБЪБФЕМСНЙ.

еУМЙ РПЛБЪБФЕМШ ЧЪБЙНОП ХЧСЪЩЧБЕФУС ФПМШЛП ДЧХНС ЛПМЙЮЕУФЧЕООП ЙЪНЕТСЕНЩНЙ ЖБЛФПТБНЙ, ФП РТЙЕН ОПУЙФ ОБЪЧБОЙЕ НЕФПДБ УЛПТТЕЛФЙТПЧБООЩИ РПЛБЪБФЕМЕК . еУМЙ ЦЕ ЮЙУМП ЖБЛФПТПЧ УПУФБЧМСЕФ ФТЙ Й ВПМЕЕ, ФП РТЙЕН РТЕПВТБЪХЕФУС Ч ГЕРОЩЕ РПДУФБОПЧЛЙ. ч ЙИ ПУОПЧЕ МЕЦЙФ РТЙЕН ЛПТТЕЛФЙТПЧЛЙ ВБЪЙУОЩИ ЪОБЮЕОЙК ЖБЛФПТПЧ ОБ ЖБЛФЙЮЕУЛЙЕ.

уРПУПВ УЛПТТЕЛФЙТПЧБООЩИ РПЛБЪБФЕМЕК РТЕДУФБЧМСЕФ ДПУФБФПЮОП РТПУФХА ЖБЛФПТОХА НПДЕМШ, ЗДЕ ЖБЛФПТЩ ЧЪБЙНОП ХЧСЪБОЩ БТЙЖНЕФЙЮЕУЛЙНЙ ДЕКУФЧЙСНЙ. рТЙ ЬФПН ЛПТТЕЛФЙТПЧЛЕ РПДЧЕТЗБЕФУС ЛПМЙЮЕУФЧЕООЩК (ЬЛУФЕОУЙЧОЩК) ЖБЛФПТ, Б ЛБЮЕУФЧЕООЩК (ЙОФЕОУЙЧОЩК) ЙМЙ ЧФПТПУФЕРЕООЩК ЛПМЙЮЕУФЧЕООЩК ПУФБЕФУС ВБЪЙУОЩН. чЩРПМОЙЧ БТЙЖНЕФЙЮЕУЛПЕ ДЕКУФЧЙЕ (ХНОПЦЕОЙЕ, ДЕМЕОЙЕ) Й РПМХЮЙЧ УЛПТТЕЛФЙТПЧБООЩК РПЛБЪБФЕМШ, ДБМЕЕ ТБУУЮЙФЩЧБАФ ЧМЙСОЙЕ ЙУЛПНЩИ ЖБЛФПТПЧ. рТЙ ПРТЕДЕМЕОЙЙ ЧФПТПУФЕРЕООПУФЙ ЛПМЙЮЕУФЧЕООПЗП ЖБЛФПТБ УМЕДХЕФ ЙУИПДЙФШ ЙЪ ЕЗП ЪОБЮЙНПУФЙ ОБ ПУОПЧЕ ЬЛУРЕТФОПК ПГЕОЛЙ.

дМС ПРТЕДЕМЕОЙС ЧМЙСОЙС ЛПМЙЮЕУФЧЕООПЗП (ЬЛУФЕОУЙЧОПЗП) ЖБЛФПТБ УМЕДХЕФ ЙЪ РПМХЮЕООПЗП УЛПТТЕЛФЙТПЧБООПЗП ЧЩЮЕУФШ ВБЪЙУОЩК (РМБОПЧЩК, ОПТНБФЙЧОЩК) РПЛБЪБФЕМШ. дМС ТБУЮЕФБ ЧМЙСОЙС ЛБЮЕУФЧЕООПЗП (ЙОФЕОУЙЧОПЗП) ЖБЛФПТБ (ЙМЙ ЧФПТПУФЕРЕООПЗП ЛПМЙЮЕУФЧЕООПЗП) УМЕДХЕФ ЙЪ ЖБЛФЙЮЕУЛПЗП РПЛБЪБФЕМС ЧЩЮЕУФШ УЛПТТЕЛФЙТПЧБООЩК. уХННБ ЧМЙСОЙС ЛПМЙЮЕУФЧЕООПЗП Й ЛБЮЕУФЧЕООПЗП ЖБЛФПТПЧ ДПМЦОБ ВЩФШ ТБЧОБ УХННЕ ПВЭЕЗП ПФЛМПОЕОЙС.

нПДЕМШ-ТБУЮЕФ ЧМЙСОЙС ЖБЛФПТПЧ РТЕДУФБЧМЕОБ Ч ФБВМЙГЕ 1.

фБВМЙГБ 1 —

нПДЕМШ-ТБУЮЕФ ЧМЙСОЙС ЖБЛФПТПЧ НЕФПДПН УЛПТТЕЛФЙТПЧБООЩИ РПЛБЪБФЕМЕК

&nbsp	рПЛБЪБФЕМЙ	вБЪЙУОЩК ЗПД	пФЮЕФОЩК ЗПД	уЛПТТЕЛФЙТПЧБООЩК РПЛБЪБФЕМШ
1	лПМЙЮЕУФЧЕООЩК ЖБЛФПТ (A)	A0	A1	A1
2	лБЮЕУФЧЕООЩК ЖБЛФПТ(в) (ЙМЙ ЧФПТПУФЕРЕООЩК ЛПМЙЮЕУФЧЕООЩК ЖБЛФПТ)	в0	в1	в0
3	рПЛБЪБФЕМШ (р)	р0	р1	рУ

чМЙСОЙЕ ЛПМЙЮЕУФЧЕООПЗП ЖБЛФПТБ: р У — р П

чМЙСОЙЕ ЛБЮЕУФЧЕООПЗП ЙМЙ ЧФПТПУФЕРЕООПЗП ЛПМЙЮЕУФЧЕООПЗП ЖБЛФПТПЧ: р 1 — р У

пВЭЕЕ ПФЛМПОЕОЙЕ: (р 1 — р 0 )

рТЙНЕТ 1: тБУУЮЙФБФШ ЧМЙСОЙЕ ЖБЛФПТПЧ ОБ ЧЩРХУЛ РТПДХЛГЙЙ РП ФБВМЙГЕ 2.

фБВМЙГБ 2 —

тБУЮЕФ ЧМЙСОЙС ЖБЛФПТПЧ ОБ ЧЩРХУЛ РТПДХЛГЙЙ

&nbsp	рПЛБЪБФЕМЙ	еДЙОЙГБ ЙЪНЕТЕОЙС	вБЪЙУОЩК ЗПД	пФЮЕФОЩК ЗПД	уЛПТТЕЛФЙТПЧБООЩК РПЛБЪБФЕМШ
1	юЙУМЕООПУФШ ТБВПФОЙЛПЧ	юЕМ.	12	10	10
2	рТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ	нМО. ТХВ.	3	3,8	3
3	чЩРХУЛ РТПДХЛГЙЙ	нМО. ТХВ.	36	38	30

чМЙСОЙЕ ЖБЛФПТПЧ:

1. юЙУМЕООПУФЙ ТБВПЮЙИ: 30 — 36 = -6

2. рТПЙЪЧПДЙФЕМШОПУФЙ ФТХДБ: 38 — 30 = +8

пВЭЕЕ ПФЛМПОЕОЙЕ: 38 -36 = +2

пФТЙГБФЕМШОЩЕ ЪОБЮЕОЙС РПЛБЪБФЕМЕК РП УНЩУМХ ТБУУНБФТЙЧБАФУС ЛБЛ ОЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ХМХЮЫЕОЙС ТБВПФЩ. ч ОБЫЕН РТЙНЕТЕ -6.

чЩЧПДЩ: чЩРХУЛ РТПДХЛГЙЙ ОБ РТЕДРТЙСФЙЙ ХЧЕМЙЮЙМУС ОБ 2 НМО. ТХВМЕК Й ТПУФ ЬФПФ ВЩМ ПВЕУРЕЮЕО Ч ПУОПЧОПН ЪБ УЮЕФ ТПУФБ РТПЙЪЧПДЙФЕМШОПУФЙ ФТХДБ. оБ РТЕДРТЙСФЙЙ ВЩМЙ ЧОЕДТЕОЩ ТБГЙПОБМЙЪБФПТУЛЙЕ РТЕДМПЦЕОЙС ТБВПФОЙЛПЧ, УПЛТБЭЕОЩ РПФЕТЙ ТБВПЮЕЗП ЧТЕНЕОЙ, ЙЪНЕОЕО ЗТБЖЙЛ ТБВПФЩ ЙОУФТХНЕОФБМШОПК ЛМБДПЧПК, ЮФП РПЪЧПМЙМП РПЧЩУЙФШ РТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ.

оЕУНПФТС ОБ ЬФП ОЕЙУРПМШЪПЧБООЩК ТЕЪЕТЧ ХЧЕМЙЮЕОЙС ПВЯЕНПЧ РТПЙЪЧПДУФЧБ УПУФБЧЙМ 6 НМО. Й ПВХУМПЧМЕО ХИПДПН У РТЕДРТЙСФЙС ЧЩУПЛПЛЧБМЙЖЙГЙТПЧБООПЗП ВТЙЗБДЙТБ Й УМЕУБТС 6 ТБЪТСДБ.

ч ГЕМСИ ОЕДПРХЭЕОЙС ХИПДБ У РТПЙЪЧПДУФЧБ ОХЦОЩИ РТЕДРТЙСФЙА УРЕГЙБМЙУФПЧ ОЕПВИПДЙНП: ХМХЮЫЙФШ ХУМПЧЙС ФТХДБ, ПРФЙНЙЪЙТПЧБФШ ПРМБФХ ФТХДБ Й Ф.Д.

нОПЗПЖБЛФПТОБС ЪБЧЙУЙНПУФШ ДПУФБФПЮОП ЮБУФП ЧУФТЕЮБЕФУС Ч РТБЛФЙЮЕУЛЙИ ТБУЮЕФБИ. оБЙВПМШЫЕК РПРХМСТОПУФША Ч ФБЛЙИ ТБУЮЕФБИ РПМШЪХЕФУС РТЙЕН ГЕРОЩИ РПДУФБОПЧПЛ. еЗП НПДЕМШ-ТБУЮЕФ РТЕДУФБЧМЕО Ч ФБВМЙГЕ 3.

фБВМЙГБ 3 —

нПДЕМШ-ТБУЮЕФ ЧМЙСОЙС ЖБЛФПТПЧ НЕФПДПН ГЕРОЩИ РПДУФБОПЧПЛ.

&nbsp	жБЛФПТЩ	хУМПЧОПЕ ПВПЪОБЮЕОЙЕ	вБЪЙУОЩК РЕТЙПД	пФЮЕФОЩК РЕТЙПД	рПДУФБОПЧЛЙ
					I	II	III
1	лПМЙЮЕУФЧЕООЩК ЖБЛФПТ	б	б0	б1	б1	б1	б1
2	лПМЙЮЕУФЧЕООЩК ЖБЛФПТ	в	в0	в1	в0	в1	в1
3	лПМЙЮЕУФЧЕООЩК ЖБЛФПТ	ч	ч0	ч1	ч0	ч0	ч1
4	лБЮЕУФЧЕООЩК ЖБЛФПТ	д	д0	д1	д0	д0	д0
5	рПЛБЪБФЕМЙ	&nbsp	р0	р1	рУЛ	рУЛ	рУЛ

лБЛ ЧЙДОП ЙЪ ФБВМЙГЩ, Ч РТПГЕУУЕ РПДУФБОПЧПЛ ЙДЕФ РПУМЕДПЧБФЕМШОБС ЪБНЕОБ ЖБЛФПТПЧ. ч РЕТЧПК РПДУФБОПЧЛЕ ЪБНЕОЈО РЕТЧЩК ВБЪЙУОЩК ЖБЛФПТ ОБ ЕЗП ЪОБЮЕОЙЕ Ч ПФЮЕФОПН РЕТЙПДЕ. уПРПУФБЧМСС ЙФПЗПЧЩК РПЛБЪБФЕМШ Ч РЕТЧПК РПДУФБОПЧЛЕ I р УЛ Й ВБЪЙУОЩК р 0 , НЩ РПМХЮБЕН ТБЪНЕТ ЧМЙСОЙС РЕТЧПЗП ЖБЛФПТБ, Ф.Л. ЙНЕООП Ч ЬФПН ЖБЛФПТЕ ЪБЛМАЮЕОП ТБЪМЙЮЙЕ ЙФПЗПЧЩИ ЪОБЮЕОЙК РПЛБЪБФЕМЕК РЕТЧПК РПДУФБОПЧЛЙ р УЛ Й р 0 . фБЛЙН ПВТБЪПН, РТЙОСЧ ХУМПЧЙЕ, ЮФП ЧМЙСОЙЕ РТПЮЙИ ЖБЛФПТПЧ, ЛТПНЕ ЙУЛПНПЗП, ЙУЛМАЮЕОП (ЬМЙНЙОЙТПЧБОП), ПРТЕДЕМСЕН ТБЪНЕТ ЕЗП ЧМЙСОЙС ОБ РПЛБЪБФЕМШ.

ч УМЕДХАЭЕК РПДУФБОПЧЛЕ ЪБНЕОЕ РПДЧЕТЗБЕФУС УМЕДХАЭЙК (ЧФПТПК) ЖБЛФПТ, Ф.Е. ЕЗП ВБЪЙУОПЕ ЪОБЮЕОЙЕ ЪБНЕОСЕФУС ОБ ПФЮЕФОПЕ (ЖБЛФЙЮЕУЛПЕ). чУЕ ПУФБМШОЩЕ ЖБЛФПТЩ РЕТЕОПУСФУС ЙЪ РТЕДЩДХЭЕК (РЕТЧПК) РПДУФБОПЧЛЙ ВЕЪ ЙЪНЕОЕОЙС. ьФП ПЪОБЮБЕФ, ЮФП РЕТЧЩК ЖБЛФПТ РЕТЕОПУЙФУС ЖБЛФЙЮЕУЛЙН (ПФЮЕФОЩН) ЕЗП ЪОБЮЕОЙЕН, ФТЕФЙК Й ЮЕФЧЕТФЩК — ВБЪЙУОЩНЙ. ч ТЕЪХМШФБФЕ ЙФПЗПЧЩК УЛПТТЕЛФЙТПЧБООЩК РПЛБЪБФЕМШ ЧП ЧФПТПК РПДУФБОПЧЛЕ ВХДЕФ ПФМЙЮБФШУС ПФ РТЕДЩДХЭЕК РПДУФБОПЧЛЙ ФПМШЛП ПДОЙН ЖБЛФПТПН — в. дМС ПРТЕДЕМЕОЙС ТБЪНЕТБ ЕЗП ЧМЙСОЙС ОБ РПЛБЪБФЕМШ ОЕПВИПДЙНП ПФ УХННЩ РПЛБЪБФЕМС ЧП ЧФПТПК РПДУФБОПЧЛЕ ЧЩЮЕУФШ РПЛБЪБФЕМШ РЕТЧПК РПДУФБОПЧЛЙ.

II р УЛ — I р УЛ

ч ФТЕФШЕК РПДУФБОПЧЛЕ ЪБНЕОЕ РПДЧЕТЗБЕФУС ФТЕФЙК ЖБЛФПТ — ч, Б ПУФБМШОЩЕ ЖБЛФПТЩ ВЕТХФУС ЛБЛ Й Ч РТЕДЩДХЭЕК РПДУФБОПЧЛЕ. тБЪНЕТ ЕЗП ЧМЙСОЙС ТБУУЮЙФЩЧБЕФУС ЛБЛ ТБЪОПУФШ НЕЦДХ УЛПТТЕЛФЙТПЧБООЩНЙ РПЛБЪБФЕМСНЙ ФТЕФШЕК Й ЧФПТПК РПДУФБОПЧПЛ: III р УЛ — II р УЛ . уМЕДПЧБФЕМШОП РТПГЕУУ ТБУЮЕФБ ЧМЙСОЙС ЖБЛФПТПЧ УПУФПЙФ Ч ФПН, ЮФП ПФ РПЛБЪБФЕМС ЛБЦДЩК РПУМЕДХАЭЕК РПДУФБОПЧЛЙ ЧЩЮЙФБЕФУС РПЛБЪБФЕМШ РТЕДЩДХЭЕК, ЛПФПТЩЕ ПФМЙЮБАФУС ДТХЗ ПФ ДТХЗБ ФПМШЛП ПДОЙН ЖБЛФПТПН, ЧМЙСОЙЕ ЛПФПТПЗП Й ПРТЕДЕМСЕФУС.

фБЛЙН ПВТБЪПН, ЮЙУМП РПДУФБОПЧПЛ ЧУЕЗДБ ВХДЕФ УПУФБЧМСФШ n — 1, Ф.Л. Ч РПУМЕДОЕК РПДУФБОПЧЛЕ РПМХЮБАФУС ЧУЕ ЖБЛФЙЮЕУЛЙЕ (ПФЮЕФОЩЕ) ЪОБЮЕОЙС ЖБЛФПТПЧ. дМС ПРТЕДЕМЕОЙС ЧМЙСОЙС РПУМЕДОЕЗП ЖБЛФПТБ Ч НПДЕМСИ У МАВЩН ЙИ ЛПМЙЮЕУФЧПН УМЕДХЕФ ЙЪ ЖБЛФЙЮЕУЛПЗП (ПФЮЕФОПЗП) ЪОБЮЕОЙС РПЛБЪБФЕМС ЧЩЮЕУФШ УХННХ РПЛБЪБФЕМС РПУМЕДОЕК РПДУФБОПЧЛЙ.

уМПЦЕОЙЕ ТБЪНЕТПЧ ЧМЙСОЙС ЧУЕИ ЖБЛФПТПЧ ДПМЦОП ДБФШ УХННХ ПВЭЕЗП ПФЛМПОЕОЙС. еУМЙ ТБЧЕОУФЧБ ОЕ ВХДЕФ, ФП УМЕДХЕФ ЙУЛБФШ ПЫЙВЛХ Ч ТБУЮЕФБИ.

чБЦОЩН ХУМПЧЙЕН РПДУФБОПЧПЛ СЧМСЕФУС УПВМАДЕОЙЕ РТБЧЙМБ : ЛБЦДБС ТСДПН УФПСЭБС РПДУФБОПЧЛБ ДПМЦОБ ПФМЙЮБФШУС ФПМШЛП ПДОЙН ЖБЛФПТПН, ЧМЙСОЙЕ ЛПФПТПЗП Й ОБИПДЙФУС.

рТЙНЕТ 2. тБУУЮЙФБФШ ЧМЙСОЙЕ ЖБЛФПТПЧ ОБ ЧЩРХУЛ РТПДХЛГЙЙ РП БМЗПТЙФНХ:

чр = ют &times юд &times л_УН &times рф

фБВМЙГБ 4 —

тБУЮЕФ ЧМЙСОЙС ЖБЛФПТПЧ ОБ ЧЩРХУЛ РТПДХЛГЙЙ НЕФПДПН ГЕРОЩИ РПДУФБОПЧПЛ

&nbsp	рПЛБЪБФЕМЙ	еД. ЙЪН.	вБЪПЧЩК ЗПД	пФЮЕФОЩК ЗПД	рПДУФБОПЧЛЙ
					I	II	III	IV
1	2	3	4	5	6	7	8	9
1	юЙУМЕООПУФШ ТБВПФОЙЛПЧ, ют	ЮЕМ.	20	18	18	18	18	18
2	юЙУМП ДОЕК, юд	ДЕОШ	25	21	25	21	21	21
3	лПЬЖЖЙГЙЕОФ УНЕООПУФЙ, лУН	л	2	1,5	2	2	1,5	1,5
4	чЩТБВПФЛБ ОБ 1 ТБВПФОЙЛБ, рф	НМО.ТХВ.	3	4	3	3	3	4
&nbsp	чЩРХУЛ РТПДХЛГЙЙ, чр	НМО.ТХВ.	3000	2268	2700	2268	1701	2268

чМЙСОЙЕ ЖБЛФПТПЧ:	&nbsp
1. юЙУМЕООПУФЙ ТБВПФОЙЛПЧ:	зт6 -зт4 = 2700 — 3000 = — 300
2. юЙУМЕООПУФЙ ДОЕК:	зт7 — зт6 = 2268 — 2700 = — 432
3. лПЬЖЖЙГЙЕОФ УНЕООПУФЙ:	зт8 -зт7 = 1701 — 2268 = — 567
4. чЩТБВПФЛБ ОБ 1 ТБВПЮЕЗП:	зт9 — зт8 = 2268 — 1701 = + 567
пВЭЕЕ ПФЛМПОЕОЙЕ:	2268 — 3000 = -732
рТПЧЕТЛБ РТБЧЙМШОПУФЙ ТБУЮЕФПЧ:	(-300) + (-432) + (-567) + 567 = -732

чЩЧПДЩ: Ч ПФЮЕФОПН РЕТЙПДЕ ЧЩРХУЛ РТПДХЛГЙЙ ЪОБЮЙФЕМШОП УОЙЪЙМУС Й УПУФБЧЙМ 2268 НМО. ТХВ., Ч ФП ЧТЕНС, ЛБЛ Ч ВБЪЙУОПН РЕТЙПДЕ ПО ВЩМ ЧЩЫЕ ОБ 732 НМО. ТХВ. хИПД У РТПЙЪЧПДУФЧБ ЧЩУПЛПЛЧБМЙЖЙГЙТПЧБООЩИ ТБВПФОЙЛПЧ РТЙЧЕМ Л РПФЕТЕ ПВЯЕНПЧ РТПЙЪЧПДУФЧБ Ч ТБЪНЕТЕ 300 НМО. ТХВ. йЪ-ЪБ ПФУХФУФЧЙС ПВЯЕНПЧ ТБВПФ ЪБЧПД ЧЩОХЦДЕО УПЛТБФЙФШ ТБВПЮХА ОЕДЕМА — ЬФП РТЙЧЕМП Л РПФЕТЕ ПВЯЕНБ РТПЙЪЧПДУФЧБ Ч ТБЪНЕТЕ 432 НМО. ТХВ, Й УПЛТБФЙФШ ЮЙУМП УНЕО У 2 ДП 1.5, ЮФП РТЙЧЕМП Л УОЙЦЕОЙА ПВЯЕНПЧ РТПЙЪЧПДУФЧБ ОБ 567 НМО. ТХВ.

дЕКУФЧЙЕ ОЕЗБФЙЧОЩИ ЖБЛФПТПЧ ПВПЫМПУШ ЪБЧПДХ УПЛТБЭЕОЙЕН ПВЯЕНПЧ РТПЙЪЧПДУФЧБ Ч ТБЪНЕТЕ 1299 НМО. ТХВ., ЮФП Й УПУФБЧМСЕФ ОЕЙУРПМШЪПЧБООЩК ТЕЪЕТЧ. й ФПМШЛП ВМБЗПДБТС ТПУФХ РТПЙЪЧПДЙФЕМШОПУФЙ ФТХДБ ЪБ УЮЕФ ЧОЕДТЕОЙС ТБГЙПОБМЙЪБФПТУЛЙИ РТЕДМПЦЕОЙК, ТЕПТЗБОЙЪБГЙЙ ТБВПЮЙИ НЕУФ Й ДТ. ЪБЧПД ДПРПМОЙФЕМШОП ЧЩРХУФЙМ РТПДХЛГЙЙ ОБ 567 НМО. ТХВ. ч ГЕМСИ НПВЙМЙЪБГЙЙ ТЕЪЕТЧПЧ ОЕПВИПДЙНП ХМХЮЫЙФШ ХУМПЧЙС ФТХДБ, ПРФЙНЙЪЙТПЧБФШ ПРМБФХ ФТХДБ, ХМХЮЫЙФШ НБТЛЕФЙОЗПЧЩЕ ЙУУМЕДПЧБОЙС ТЩОЛБ.

йОФЕЗТБМШОЩК НЕФПД РТЙНЕОСЕФУС Ч БМЗПТЙФНБИ РПЛБЪБФЕМЕК, УПУФПСЭЙИ ЙЪ ДЧХИ ЖБЛФПТПЧ. рТЙ ЬФПН ЖБЛФПТЩ ОЕ ФТЕВХЕФУС ЛМБУУЙЖЙГЙТПЧБФШ ОБ ЛПМЙЮЕУФЧЕООЩЕ (ЬЛУФЕОУЙЧОЩЕ) Й ЛБЮЕУФЧЕООЩЕ (ЙОФЕОУЙЧОЩЕ), ЛБЛ ЬФП ДЕМБЕФУС РТЙ ЙУРПМШЪПЧБОЙЙ ДТХЗЙИ РТЙЕНПЧ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ. ьФП ПВХУМПЧМЕОП УХЭОПУФША РТЙЕНБ, ЛПФПТБС УПУФПЙФ Ч ФПН, ЮФП РТЙТПУФ ЛБЦДПЗП ЙЪ ЖБЛФПТПЧ ТБУРТЕДЕМСЕФУС НЕЦДХ РПЛБЪБФЕМСНЙ РТПРПТГЙПОБМШОП. чМЙСОЙЕ РЕТЧПЗП ЖБЛФПТБ ПРТЕДЕМСЕФУС ХНОПЦЕОЙЕН ЕЗП РТЙТПУФБ ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ ДТХЗПЗП ЖБЛФПТБ. чМЙСОЙЕ ЦЕ ЧФПТПЗП ЖБЛФПТБ ПРТЕДЕМСЕФУС ХНОПЦЕОЙЕН ЕЗП РТЙТПУФБ ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ РЕТЧПЗП ЖБЛФПТБ. чПЪОЙЛЫЙК Ч ТБУЮЕФБИ ОЕДЕМЙНЩК ПУФБФПЛ ТБУРТЕДЕМСЕФУС НЕЦДХ ЖБЛФПТБНЙ РПТПЧОХ:0,5* (РТЙТПУФ РЕТЧПЗП ЖБЛФПТБ * РТЙТПУФ ЧФПТПЗП ЖБЛФПТБ). рП НОЕОЙА ПДОЙИ ЬЛПОПНЙУФПЧ ФБЛЙН РХФЕН ПВЕУРЕЮЙЧБЕФУС ВПМЕЕ ФПЮОПЕ ПРТЕДЕМЕОЙЕ ТБЪНЕТБ ЧМЙСОЙС ЖБЛФПТПЧ. рП НОЕОЙА ДТХЗЙИ — МАВПК ЙЪ НЕФПДПЧ ТБУЮЕФПЧ ОЕ ДБЕФ ДПУФБФПЮОП ФПЮОЩИ ТЕЪХМШФБФПЧ ЧЩЮЙУМЕОЙК, ЮФП ПВХУМПЧМЙЧБЕФ РПЗТЕЫОПУФЙ Ч ТБУЮЕФБИ. тБУЮЕФЩ ЧМЙСОЙС ЖБЛФПТПЧ ОБ РПЛБЪБФЕМШ ЧЩРХУЛБ РТПДХЛГЙЙ ЙОФЕЗТБМШОЩН НЕФПДПН РТПЧЕДЕОЩ РП ДБООЩН ФБВМЙГЩ 5.

фБВМЙГБ 5-

йУИПДОЩЕ ДБООЩЕ ДМС ТБУЮЕФБ ЧМЙСОЙС ЬЛУФЕОУЙЧОЩИ Й ЙОФЕОУЙЧОЩИ ЖБЛФПТПЧ ЙУРПМШЪПЧБОЙС ФТХДБ ОБ ПВЭЙК ПВЯЕН РТПЙЪЧПДУФЧБ

&nbsp	рПЛБЪБФЕМЙ	еД. ЙЪН.	вБЪЙУОЩК ЗПД	пФЮЕФОЩК ЗПД	ПФЛМПОЕОЙС
1	юЙУМЕООПУФШ ТБВПФОЙЛПЧ	ЮЕМ.	20	25	5
2	рТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ	ФЩУ. ТХВ.	16	15	-1
3	чЩРХУЛ РТПДХЛГЙЙ	ФЩУ. ТХВ.	320	375	55

жБЛФПТОЩК БОБМЙЪ РТЕДХУНБФТЙЧБЕФ УМЕДХАЭЙЕ ЬФБРЩ ТБУЮЕФПЧ:

1. чМЙСОЙЕ ОБ ЧЩРХУЛ РТПДХЛГЙЙ ЙЪНЕОЕОЙК РП РЕТЧПНХ ЖБЛФПТХ ТБУУЮЙФЩЧБЕФУС РХФЕН ХНОПЦЕОЙС ЕЗП РТЙТПУФБ ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ ЧФПТПЗП ЖБЛФПТБ Й РТЙВБЧМЕОЙС Л ОЙН РПМПЧЙОЩ ОЕТБЪМПЦЙНПЗП ПУФБФЛБ: (+5)*16 + 0,5[(+5) * (-1)] = +77,5

2. чМЙСОЙЕ ЧФПТПЗП ЖБЛФПТБ ТБУУЮЙФЩЧБЕФУС РХФЕН ХНОПЦЕОЙС ЕЗП РТЙТПУФБ ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ РЕТЧПЗП ЖБЛФПТБ Й РТЙВБЧМЕОЙС Л ОЙН РПМПЧЙОЩ ОЕТБЪМПЦЙНПЗП ПУФБФЛБ: (-1)*20 + 0,5[(+5) * (-1)] = -22,5

пВЭЕЕ ПФЛМПОЕОЙЕ УПУФБЧЙФ: (375 -320)=55; (77,5) + (-22,5) = 55

оЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ РТЙТПУФБ РТПДХЛГЙЙ УПУФБЧЙМЙ 22,5 ФЩУ. ТХВ. дМС УТБЧОЕОЙС ЬЖЖЕЛФЙЧОПУФЙ ЙУРПМШЪХЕНЩИ РТЙЕНПЧ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ Й ТЕЪХМШФБФПЧ ТБУЮЕФПЧ ТБУУНПФТЕОЙЕ УМЕДХАЭЕЗП ЙОДЕЛУОПЗП НЕФПДБ РТПЧЕДЕОП ОБ ПДЙОБЛПЧЩИ ЙУИПДОЩИ ДБООЩИ ФБВМЙГЩ 5.

йОДЕЛУОЩК НЕФПД РТЙНЕОСЕФУС Ч ТБУЮЕФБИ, Ч БМЗПТЙФНБИ ЛПФПТЩИ ХЧСЪЩЧБАФУС ФПМШЛП ДЧБ ЖБЛФПТБ, РТЙЮЕН ФПМШЛП УП ЪОБЛПН ХНОПЦЕОЙС. пЗТБОЙЮЕООПУФШ ЕЗП РТЙНЕОЕОЙС РТЙ РЕТЕЮЙУМЕООЩИ ХУМПЧЙСИ СЧМСЕФУС УХЭЕУФЧЕООЩН ОЕДПУФБФЛПН. тБУЮЕФЩ РТЙ ЙОДЕЛУОПН НЕФПДЕ ОБЮЙОБАФУС У ЛМБУУЙЖЙЛБГЙЙ ЖБЛФПТПЧ ОБ ЬЛУФЕОУЙЧОЩЕ (ЛПМЙЮЕУФЧЕООЩЕ) Й ЙОФЕОУЙЧОЩЕ (ЛБЮЕУФЧЕООЩЕ) Й Ч ЪБЧЙУЙНПУФЙ ПФ ЬФПЗП РТЙНЕОСЕФУС ФЕИОЙЛБ ЧЩЮЙУМЕОЙК ЙИ ЧМЙСОЙС ОБ РПЛБЪБФЕМШ.

чМЙСОЙЕ ЬЛУФЕОУЙЧОПЗП (ЛПМЙЮЕУФЧЕООПЗП) ЖБЛФПТБ ПРТЕДЕМСЕФУС ХНОПЦЕОЙЕН ЕЗП РТЙТПУФБ ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ ЙОФЕОУЙЧОПЗП (ЛБЮЕУФЧЕООПЗП) ЖБЛФПТБ. чМЙСОЙЕ ЙОФЕОУЙЧОПЗП (ЛБЮЕУФЧЕООПЗП) ЖБЛФПТБ ПРТЕДЕМСЕФУС ХНОПЦЕОЙЕН ЕЗП РТЙТПУФБ ОБ ПФЮЕФОПЕ ЪОБЮЕОЙЕ ЬЛУФЕОУЙЧОПЗП (ЛПМЙЮЕУФЧЕООПЗП) ЖБЛФПТБ. уХННБ ЧМЙСОЙС ЖБЛФПТПЧ ДПМЦОБ ВЩФШ ТБЧОБ УХННЕ ПВЭЕЗП ПФЛМПОЕОЙС. тЕЪЕТЧЩ ПРТЕДЕМСАФУС РП ПВЭЙН РТБЧЙМБН. ч РТЙЧЕДЕООПН РТЙНЕТЕ ЖБЛФПТ ЮЙУМЕООПУФЙ ТБВПФОЙЛПЧ СЧМСФУС ЛПМЙЮЕУФЧЕООЩН ЙМЙ ЬЛУФЕОУЙЧОЩН, Б ЖБЛФПТ РТПЙЪЧПДЙФЕМШОУФЙ ФТХДБ — ЛБЮЕУФЧЕООЩН ЙМЙ ЙОФЕОУЙЧОЩН.

чМЙСОЙЕ ЖБЛФПТПЧ:

1. ьЛУФЕОУЙЧОПЗП = ЕЗП РТЙТПУФ ХНОПЦБЕФУС ОБ ВБЪЙУОПЕ ЪОБЮЕОЙЕ ЙОФЕОУЙЧОПЗП ЖБЛФПТБ: 5*16 = +80

2. йОФЕОУЙЧОПЗП = ЕЗП РТЙТПУФ ХНОПЦБЕФУС ОБ ПФЮЕФОПЕ ЪОБЮЕОЙЕ ЬЛУФЕОУЙЧОПЗП ЖБЛФПТБ: (-1)*25 = -25

пВЭЕЕ ПФЛМПОЕОЙЕ УПУФБЧЙФ: 375 -320 = 55; РТПЧЕТЛБ ЕЗП ДЕМБЕФУС УХННЙТПЧБОЙЕН ЪОБЮЕОЙК ЧМЙСОЙС ЖБЛФПТПЧ: (+80) + (-25)= +55

оЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ХЧЕМЙЮЕОЙС РТПЙЪЧПДУФЧБ РТПДХЛГЙЙ УПУФБЧЙМЙ 25 ФЩУ. ТХВ.

фБЛЙН ПВТБЪПН, ТЕЪХМШФБФЩ ТБУЮЕФБ ЧМЙСОЙС ЖБЛФПТПЧ РТЙ ЙУРПМШЪПЧБОЙЙ ЙОФЕЗТБМШОПЗП Й ЙОДЕЛУОПЗП НЕФПДПЧ РПМХЮБАФУС ТБЪОЩНЙ. оП РПУЛПМШЛХ, ТБЪОЙГБ ЬФБ ОЕУХЭЕУФЧЕООБС, Б ИБТБЛФЕТ ЧМЙСОЙС ЖБЛФПТПЧ ПУФБЕФУС ПДОПЪОБЮОЩН, ПВБ НЕФПДБ ЫЙТПЛП ЙУРПМШЪХАФУС Ч БОБМЙФЙЮЕУЛЙИ ТБУЮЕФБИ.

рТЙЕН ВБМБОУПЧПК ХЧСЪЛЙ ПУОПЧБО ОБ ЧЪБЙНПУЧСЪЙ ПУФБФЛПЧ ГЕООПУФЕК (ЪБДПМЦЕОПУФЙ), РТЙИПДБ (ХЧЕМЙЮЕОЙС ЙИ), ТБУИПДБ (ХНЕОШЫЕОЙС ЙИ). рТЙ ЬФПН ТБУИПД НПЦЕФ ЧЛМАЮБФШ ТБЪОЩЕ РП ЬЛПОПНЙЮЕУЛПНХ УПДЕТЦБОЙА ЧЙДЩ ЧЩВЩФЙС. ьФП НПЗХФ ВЩФШ МЙВП ТЕБМЙЪБГЙС, МЙВП РТПЮЕЕ ЧЩВЩФЙЕ: ВПК, МПН, РПТЮБ, ОЕДПУФБЮБ, ВТБЛ, ЧОХФТЕООЙК ПФРХУЛ, Ф.Е. РЕТЕНЕЭЕОЙЕ ПФ ПДОПЗП НБФЕТЙБМШОП-ПФЧЕФУФЧЕООПЗП МЙГБ Л ДТХЗПНХ ЛБЛЙИ-МЙВП ГЕООПУФЕК.

пВЭЙК ЧЙД ВБМБОУПЧПК ХЧСЪЛЙ РТЕДУФБЧМЕО Ч ЖПТНХМЕ:

п О + р = т + ч РТПЮ. + п Л , ЗДЕ

п О — ПУФБФПЛ ОБ ОБЮБМП;

п Л — ПУФБФПЛ ОБ ЛПОЕГ;

ч РТПЮ. — РТПЮЕЕ ЧЩВЩФЙЕ.

ч ЪБЧЙУЙНПУФЙ ПФ ГЕМЙ БОБМЙЪБ ЖБЛФПТЩ Й РПЛБЪБФЕМЙ НПЗХФ РПНЕОСФШУС НЕУФБНЙ. еУМЙ РПЛБЪБФЕМЕН ВХДЕФ ТЕБМЙЪБГЙС (т), ФПЗДБ ЧУЕ ПУФБМШОЩЕ ЬМЕНЕОФЩ ВБМБОУПЧПК ХЧСЪЛЙ ВХДХФ ЖБЛФПТБНЙ: т = п О + р — ч РТПЮ. — п Л тБУЮЕФ РТЕДУФБЧМЕО Ч ФБВМЙГЕ 6.

фБВМЙГБ 6 —

тБУЮЕФ ЧМЙСОЙС РПЛБЪБФЕМЕК ВБМБОУПЧПК ХЧСЪЛЙ (ФПЧБТОПЗП ВБМБОУБ) ОБ ТЕБМЙЪБГЙА

&nbsp	рПЛБЪБФЕМЙ	вБЪЙУОЩК ЗПД	пФЮЕФОЩК ЗПД	пФЛМПОЕОЙС	чМЙСОЙЕ ЖБЛФПТПЧ
1	пУФБФПЛ ОБ ОБЮБМП	160	170	+ 10	+ 10
2	рТЙИПД	500	480	— 20	— 20
3	рТПЮЕЕ ЧЩВЩФЙЕ	30	80	+ 50	— 50
4	пУФБФПЛ ОБ ЛПОЕГ	90	45	— 45	+ 45
5	тЕБМЙЪБГЙС	540	525	— 15	— 15

тБУУЮЙФБЧ ПФЛМПОЕОЙЕ ДБООЩИ ПФЮЕФОПЗП РЕТЙПДБ ПФ ВБЪЙУОПЗП НПЦОП ХУФБОПЧЙФШ, ЮФП ТБЪНЕТ ЕЗП РП ЧУЕН ЖБЛФПТБН ОЕ УППФЧЕФУФЧХЕФ ПВЭЕНХ ПФЛМПОЕОЙА РП РПЛБЪБФЕМА ТЕБМЙЪБГЙЙ, Ф.Е. 15. юПВЩ ПРТЕДЕМЙФШ ТБЪНЕТ ЧМСОЙС ЛБЪДПЗП ЙЪ ЖБЛФПТПЧ, УМЕДХЕФ НЕФПДПН МПЗЙЮЕУЛПК ПГЕОЛЙ ПРТЕДЕМЙФШ ИБТБЛФЕТ ЧМЙСОЙС Й, УППФЧЕФУФЧЕООП, ЪОБЛ «+» ЙМЙ «-» РЕТЕД УХННПК ПФЛМПОЕОЙС РП ЛБЦДПНХ ЖБЛФПТХ. рП ЖБЛФПТХ «рТПЮЕЕ ЧЩВЩФЙЕ» ЙЪНЕОЙН ЪОБЛ ОБ РТПФЙЧПРПМПЦОЩК, РПУЛПМШЛХ ТПУФ ВТБЛБ, МПНБ. РПТЮЙ ЙНХЭЕУФЧБ Й Ф.Р. РТЙЧПДЙФ Л УОЙЦЕОЙА ТЕБМЙЪБГЙЙ. уМЕДПЧБФЕМШОП, ТПУФ УХННЩ РП ДБООПНХ ЖБЛФПТХ ОБ 50 ПФТЙГБФЕМШОП РПЧМЙСМ ОБ ТЕБМЙЪБГЙА. уОЙЦЕОЙЕ ПУФБФЛПЧ ОБ ЛПОЕГ РП УХФЙ ПЪОБЮБЕФ ХЧЕМЙЮЕОЙЕ ТЕБМЙЪПЧБООЩИ ГЕООПУФЕК Й Ч ОБЫЕН РТЙНЕТЕ ЬФПФ ЖБЛФПТ ХЧЕМЙЮЙМ ТЕБМЙЪБГЙА ОБ 45. иБТБЛФЕТ ЧМЙСОЙС ДТХЗЙИ ЖБЛФПТПЧ-ПУФБФЛПЧ ОБ ОБЮБМП Й РПУФХРМЕОЙС (РТЙИПДБ) Ч ОБЫЕН РТЙНЕТЕ УПЧРБМП У ИБТБЛФЕТПН ПФЛМПОЕОЙК Й РПЬФПНХ ЙИ ЪОБЮЕОЙЕ ЙЪ ЗТБЖЩ «пФЛМПОЕОЙЕ» РЕТЕОЕУЕОП ВЕЪ ЙЪНЕОЕОЙК Ч ЗТБЖХ «чМЙСОЙЕ ЖБЛФПТПЧ». рПДУЮЕФ ЙФПЗБ Ч ОЕК УПУФБЧМСЕФ — 15, Ф.Е. ТБЪНЕТ ПВЭЕЗП ПФЛМПОЕОЙС, ЮФП РПДФЧЕТЦДБЕФ РТБЧЙМШОПУФШ ТБУЮЕФПЧ. оЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ТПУФБ ТЕБМЙЪБГЙЙ УПУФБЧЙМЙ: (-20) + (-50) = (-70). дМС ЙИ НПВЙМЙЪБГЙЙ РТЕДРТЙСФЙА ОЕПВИПДЙНП УЧПЕЧТЕНЕООП ЪБЧПЪЙФШ ФПЧБТЩ Й ОЕ ДПРХУЛБФШ ВТБЛБ, РПТЮЙ Й Ф.Д.

нЕФПД ПФЛМПОЕОЙК ЙУРПМШЪХЕФУС Ч ТБУЮЕФБИ ДМС БВУПМАФОЩИ Й ПФОПУЙФЕМШОЩИ ЧЕМЙЮЙО. пДЙО ЙЪ ЕЗП ЧБТЙБОФПЧ РТЕДУФБЧМЕО Ч ФБВМЙГЕ 7.

еУМЙ РПЛБЪБФЕМШ Й ЖБЛФПТЩ ХЧСЪЩЧБАФУС НЕЦДХ УПВПК ЪОБЛБНЙ «РМАУ» Й «НЙОХУ», ФП ОБЙВПМЕЕ ФПЮОП НПЦОП ТБУУЮЙФБФШ ЧМЙСОЙЕ ЛБЦДПЗП ЙЪ ЖБЛФПТПЧ РЕТЕУЮЕФПН ПФЛМПОЕОЙК ЮЕТЕЪ БВУПМАФОЩЕ Й ПФОПУЙФЕМШОЩЕ ЧЕМЙЮЙОЩ (ТБЪОЙГЩ).

пФДЕМШОЩЕ БЧФПТЩ ОБЪЩЧБАФ ЬФПФ НЕФПД УРПУПВПН РТПГЕОФОЩИ ТБЪОЙГ, ИПФС УХФШ ЕЗП ЙНЕЕФ ОЕЛПФПТЩЕ ПУПВЕООПУФЙ Ч НЕФПДПМПЗЙЙ ТБУЮЕФБ РПУМЕДОЕЗП ЖБЛФПТБ (ПФ ПВЭЕЗП ПФЛМПОЕОЙС ПФОЙНБЕФУС УХННБ ЧУЕИ ТБОЕЕ ТБУУЮЙФБООЩИ ЖБЛФПТПЧ). ьФЙН ТБУЮЕФПН РП УХФЙ УЛТЩЧБАФУС ЧУЕ РПЗТЕЫОПУФЙ Ч ТБУЮЕФЕ ЧМЙСОЙС РТЕДЩДХЭЙИ ЖБЛФПТПЧ.

фПФ ЧБТЙБОФ ТБУЮЕФБ, ЛПФПТЩК РТЕДМБЗБЕФУС Ч ФБВ. 5, ОЕ ЙНЕЕФ ФБЛПК РПЗТЕЫОПУФЙ, ОП РТЕДУФБЧМСЕФУС УРПТОЩН РП ДТХЗПК РТЙЮЙОЕ. тСД УФБФЕК ДПИПДПЧ Й ТБУИПДПЧ ОЕ ЙНЕАФ РТСНПК ЪБЧЙУЙНПУФЙ ПФ ТЕБМЙЪБГЙЙ, ФЕН ОЕ НЕОЕЕ ЙЪНЕОЕОЙЕ ХТПЧОЕК РП ОЙН РЕТЕУЮЙФЩЧБЕФУС ОБ ЖБЛФЙЮЕУЛЙК ПВЯЕН РТПДБЦ. ч ЮБУФОПУФЙ, ЧОЕТЕБМЙЪБГЙПООЩЕ ДПИПДЩ Й ТБУИПДЩ, ЛПФПТЩЕ ЧЛМАЮБАФ, Ч ПУОПЧОПН, ЫФТБЖОЩЕ УБОЛГЙЙ РПМХЮЕООЩЕ, ХРМБЮЕООЩЕ Й Ф.Д.

нЕФПДПМПЗЙС ТБУЮЕФБ ЖБЛФПТПЧ, ЪБЧЙУЙНЩИ Й ОЕ ЪБЧЙУЙНЩИ ПФ ТЕБМЙЪБГЙЙ ЪБЛМАЮБЕФУС Ч УМЕДХАЭЕН:

1. чМЙСОЙЕ ПВЯЕНБ ТЕБМЙЪБГЙЙ ОБ РТЙВЩМШ ПРТЕДЕМСЕФУС ХНОПЦЕОЙЕН ПФЛМПОЕОЙС ЖБЛФЙЮЕУЛПК ТЕБМЙЪБГЙЙ ПФ ВБЪЙУОПК ЙМЙ РМБОПЧПК ЕЕ УХННЩ ОБ РМБОПЧЩК ХТПЧЕОШ ТЕОФБВЕМШОПУФЙ Й ДЕМЕОЙЕН ОБ 100%.
2. чМЙСОЙЕ ЧУЕИ ПУФБМШОЩИ ЖБЛФПТПЧ ТБУУЮЙФЩЧБЕФУС ХНОПЦЕОЙЕН ЖБЛФЙЮЕУЛПК (ПФЮЕФОПК) УХННЩ ТЕБМЙЪБГЙЙ ОБ ПФЛМПОЕОЙЕ Ч ХТПЧОСИ УППФЧЕФУФЧХАЭЕЗП ЖБЛФПТБ Й ДЕМЕОЙЕН ОБ 100%.

уХННБ ЧМЙСОЙС ЧУЕИ ЖБЛФПТПЧ ДПМЦОБ ВЩФШ ТБЧОБ ПВЭЕНХ ПФЛМПОЕОЙА, Ф.Е. ТБЪОЙГЕ ЖБЛФЙЮЕУЛПК (ПФЮЕФОПК) Й ВБЪЙУОПК (ЙМЙ РМБОПЧПК) УХННПК РТЙВЩМЙ.

фБВМЙГБ 7 —

тБУЮЕФ ЖБЛФПТПЧ, ЧМЙСАЭЙИ ОБ РТЙВЩМШ (ХВЩФПЛ).

&nbsp	рПЛБЪБФЕМЙ	вБЪЙУОЩК		пФЮЕФОЩК		пФЛМПОЕОЙС		чМЙСОЙЕ ЖБЛФПТПЧ
		УХННБ	ХД. ЧЕУ	УХННБ	ХД. ЧЕУ	Ч УХННЕ	Ч %
1	тЕБМЙЪБГЙС	200	100	240	100	+40	—	8
2	ъБФТБФЩ РТПЙЪЧПДУФЧБ	130	65	150	62,5	X	— 2,5	6
3	чОЕТЕБМЙЪБГЙПООЩЕ ДПИПДЩ	60	30	70	29,2	X	— 0,8	— 1,9
4	чОЕТЕБМЙЪБГЙПООЩЕ ХВЩФЛЙ	90	45	130	54,2	X	+ 9,2	— 22,1
5	жЙОБОУПЧЩК ТЕЪХМШФБФ:	40	20	30	12,5	— 10	— 8,5	— 10
6	РТЙВЩМШ (+)	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp
7	ХВЩФПЛ (-)	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp

чМЙСОЙЕ ЖБЛФПТПЧ:	&nbsp
1. тЕБМЙЪБГЙЙ:	[(+40) &times 20]/100 = +8
2. уЕВЕУФПЙНПУФЙ:	[240 &times (-2,5)]/100 = +6
3. чОЕТЕБМЙЪБГЙПООЩИ ДПИПДПЧ:	[240 &times (-0,8)]/100 = -1.9
4. чОЕТЕБМЙЪБГЙПООЩИ ТБУИПДПЧ:	[240 &times 9,2]/100 = -22,1
пВЭЕЕ ПФЛМПОЕОЙЕ:	-10

чЩЧПДЩ:рТЙВЩМШ Ч ПФЮЕФОПН ЗПДХ УПЛТБФЙМБУШ ОБ 10 НМО. ТХВ. оЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ЕЕ ХЧЕМЙЮЕОЙС УПУФБЧЙМЙ 24 НМО. ТХВ. (1,9 + 22,1) ЪБ УЮЕФ УПЛТБЭЕОЙС ЧОЕТЙБМЙЪБГЙПООЩИ ДПИПДПЧ Й ТПУФБ ЧОЕТЕБМЙЪБГЙПООЩИ ХВЩФЛПЧ. ьФЙ РПФЕТЙ РТЙВЩМЙ РТЕДРТЙСФЙА ХДБМПУШ УПЛТБФЙФШ ОБ 14 НМО. ТХВ. ЪБ УЮЕФ ХЧЕМЙЮЕОЙС ЧЩТХЮЛЙ ПФ ТЕБМЙЪБГЙЙ ОБ — 8 НМО. ТХВ., Й ЬЛПОПНЙЙ ЪБФТБФ ОБ РТПЙЪЧПДУФЧП — ОБ 6 НМО. ТХВ.

нЕФПД РТПГЕОФОЩИ ЮЙУЕМ РП ЛПМЙЮЕУФЧХ РТЙНЕОСЕФУС Ч ТБУЮЕФБИ, ЗДЕ ФТЕВХЕФУС ПРТЕДЕМЙФШ ЧМЙСОЙЕ ЙЪНЕОЕОЙК Ч УФТХЛФХТЕ РПЛБЪБФЕМС ОБ ЕЗП ПВЭЙК ПВЯЕН. йЪНЕОЕОЙС Ч УФТХЛФХТЕ НПЗХФ ВЩФШ УЧСЪБОЩ У ТБЪОПК ФТХДПЕНЛПУФША, БУУПТФЙНЕОФПН, Ф.Е. ЧЙДБНЙ РТПДХЛГЙЙ, Б ФБЛЦЕ ТБЪМЙЮОЩН ЕЕ ЛБЮЕУФЧПН.

уХЭОПУФШ НЕФПДБ РТПГЕОФОПЗП ЮЙУМБ РП ЛПМЙЮЕУФЧХ Й НЕФПДБ Ч ГЕМПН УПУФПЙФ Ч ФПН, ЮФП ПФЮЕФОЩК РПЛБЪБФЕМШ РП ЛПМЙЮЕУФЧХ РЕТЕУЮЙФЩЧБЕФУС ОБ ВБЪЙУОХА УФТХЛФХТХ РП БУУПТФЙНЕОФХ, ЛБЮЕУФЧХ Й Ф.Д. рТЙ ЬФПН ДЕМБЕФУС ТБУЮЕФ, ЛПФПТЩК ПФТБЦБЕФ, ЛБЛ ТБУРТЕДЕМЙМПУШ ВЩ ПВЭЕЕ ЛПМЙЮЕУФЧП РТПДХЛГЙЙ РП УФТХЛФХТЕ ВБЪЙУОПЗП РЕТЙПДБ. дМС ЬФПЗП ЙФПЗПЧПЕ ЛПМЙЮЕУФЧП РТПДХЛГЙЙ ПФЮЕФОПЗП РЕТЙПДБ ХНОПЦБЕФУС ОБ ХДЕМШОЩЕ ЧЕУБ (УФТХЛФХТХ) ЛБЦДПЗП ЕЕ ЧЙДБ.

тБЪДЕМЙЧ РПМХЮЕООПЕ РТПГЕОФОПЕ ЮЙУМП ОБ 100%, РПМХЮБЕН ЖБЛФЙЮЕУЛПЕ ЛПМЙЮЕУФЧП РТПДХЛГЙЙ, УЛПТТЕЛФЙТПЧБООПЕ ОБ ВБЪЙУОХА УФТХЛФХТХ.

дМС ПРТЕДЕМЕОЙС УХННЩ РТПДХЛГЙЙ, УЛПТТЕЛФЙТПЧБООПК ОБ ВБЪЙУОХА УФТХЛФХТХ, ОЕПВИПДЙНП ГЕОХ ПФЮЕФОПЗП РЕТЙПДБ ХНОПЦЙФШ ОБ УЛПТТЕЛФЙТПЧБООПЕ ЛПМЙЮЕУФЧП РТПДХЛГЙЙ.

чМЙСОЙЕ УФТХЛФХТЩ РПЛБЪБФЕМС (ХДЕМШОПЗП ЧЕУБ ЛПМЙЮЕУФЧБ РТПДХЛГЙЙ Ч БУУПТФЙНЕОФЕ, ФТХДПЕНЛПУФЙ, ЛБЮЕУФЧБ Й ДТ.) ПРТЕДЕМСЕФУС ЛБЛ ТБЪОПУФШ НЕЦДХ ЕЗП УХННПК ЪБ ПФЮЕФОЩК РЕТЙПД Й УЛПТТЕЛФЙТПЧБООПК УХННПК. (фБВМЙГБ 8)

фБВМЙГБ 8 —

тБУЮЕФ УФТХЛФХТЩ БУУПТФЙНЕОФБ РТПДХЛГЙЙ РП ЛБЮЕУФЧХ Й ЧМЙСОЙС ЙЪНЕОЕОЙК Ч ОЕК ОБ ПВЭЙК ПВЯЕН РТПЙЪЧПДУФЧБ

чЙДЩ РТПДХЛГЙЙ	вБЪЙУОЩЕ РПЛБЪБФЕМЙ(РМБОПЧЩЕ)				пФЮЕФОЩЕ РПЛБЪБФЕМЙ				рТПГЕОФОПЕ ЮЙУМП	лПМЙЮЕУФЧП РТПДХЛГЙЙ, УЛПТЕЛФЙТПЧБООПЕ РП ВБЪЙУОПК УФТХЛФХТЕ	уХННБ РТПДХЛГЙЙ, УЛПТТЕЛФЙТПЧБООБС РП ВБЪЙУОПК УФТХЛФХТЕ
	лПМЙЮЕУФЧП		&nbsp		лПМЙЮЕУФЧП		&nbsp
	ЫФ.	ХД. ЧЕУ.	ГЕОБ	УХННБ	ЫФ.	ХД. ЧЕУ.	ГЕОБ	УХННБ
1	2	3	4	5	6	7	8	9	10	11	12
б Ч/У	30	50	4	120	40	56	5	200	3600	36	180
б 1/У	30	50	3	90	32	44	4	128	3600	36	144
йФПЗП:	60	100	&nbsp	210	72	100	&nbsp	328	7200	72	324

чМЙСОЙЕ ЙЪНЕОЕОЙК Ч УФТХЛФХТЕ РТПДХЛГЙЙ, ТБУУЮЙФБООПК РП РПЛБЪБФЕМА ЕЕ ЛБЮЕУФЧБ, ОБ ПВЭЙК ПВЯЕН РТПЙЪЧПДУФЧБ УПУФБЧЙФ : 328 — 324 = 4. уМЕДПЧБФЕМШОП РПЧЩЫЕОЙЕ ЛБЮЕУФЧБ РТПДХЛГЙЙ Ч ПФЮЕФОПН ЗПДХ РПЪЧПМЙМП РТЕДРТЙСФЙА ХЧЕМЙЮЙФШ ПВЭЙК ПВЯЕН РТПЙЪЧПДУФЧБ ОБ 4 ФЩУ.ТХВ.

нЕФПД РТПГЕОФОЩИ ЮЙУЕМ РП УХННЕ РТЙНЕОСЕФУС Ч ТБУЮЕФБИ, ЗДЕ ОЕФ РПЛБЪБФЕМЕК ЛПМЙЮЕУФЧБ Й ГЕОЩ, ЮФП ЪОБЮЙФЕМШОП ХРТПЭБЕФ РТПГЕУУ ТБУЮЕФПЧ. юБЭЕ ЧУЕЗП ПОЙ ЧЛМАЮБАФ ОЕПВИПДЙНПУФШ ТБУУЮЙФБФШ ЧМЙСОЙЕ ЙЪНЕОЕОЙК Ч УПУФБЧЕ Й УФТХЛФХТЕ ЪБФТБФ ОБ РТПЙЪЧПДУФЧП ОБ ПВЭХА ЙИ УХННХ. (фБВМЙГБ 9)

фБВМЙГБ 9 —

тБУЮЕФ ЧМЙСОЙС УФТХЛФХТЩ РПЛБЪБФЕМС НЕФПДПН РТПГЕОФОПЗП ЮЙУМБ РП УХННЕ

рПЛБЪБФЕМЙ	вБЪЙУОЩК РПЛБЪБФЕМШ		пФЮЕФОЩК РПЛБЪБФЕМШ		рТПГЕОФОПЕ ЮЙУМП	чМЙСОЙЕ УФТХЛФХТЩ
	УХННБ	ХД. ЧЕУ	УХННБ	ХД.ЧЕУ
1	2	3	4	5	6	7
уЩТШЕ, НБФЕТЙБМЩ	120	40	180	51	14000	40
ъБТРМБФБ	80	27	90	26	9450	-4.5
бНПТФЙЪБГЙС	40	13	45	13	4550	-0.5
рТПЮЙЕ ТБУИПДЩ	60	20	35	10	7000	-35
йФПЗП:	300	100	350	&nbsp	35000	0

уХЭОПУФШ НЕФПДБ РТПГЕОФОПЗП ЮЙУМБ РП УХННЕ УПУФПЙФ Ч ФПН, ЮФП ПВЭБС УХННБ РПЛБЪБФЕМС ПФЮЕФОПЗП РЕТЙПДБ РЕТЕУЮЙФЩЧБЕФУС РП УФТХЛФХТЕ ВБЪЙУОПЗП ЙМЙ РМБОПЧПЗП. дМС ЬФПЗП ЙФПЗПЧБС УХННБ РПЛБЪБФЕМС ПФЮЕФОПЗП РЕТЙПДБ ХНОПЦБЕФУС ОБ ХДЕМШОЩЕ ЧЕУБ ЕЗП (Ф.Е. УФТХЛФХТХ) ЪБ ВБЪЙУОЩК РЕТЙПД. рПМХЮЕООПЕ РТПГЕОФОПЕ ЮЙУМП ЬЛПОПНЙЮЕУЛПЗП УНЩУМБ ОЕ ЙНЕЕФ, ОП ТБЪДЕМЕООПЕ ОБ 100% РП ЛБЦДПНХ ЧЙДХ РПЛБЪБФЕМС, ПФТБЦБЕФ ЖБЛФЙЮЕУЛХА УХННХ ЕЗП, ЛПФПТБС НПЗМБ ВЩ УМПЦЙФШУС РТЙ ВБЪЙУОПК УФТХЛФХТЕ.

дМС ТБУЮЕФБ ЧМЙСОЙС УФТХЛФХТЩ ОЕПВИПДЙНП ПФ РПЛБЪБФЕМС ЪБ ПФЮЕФОЩК РЕТЙПД РП ЛБЦДПНХ ЧЙДХ (РП УФБФШСН ЪБФТБФ) ПФОСФШ РТПГЕОФОПЕ ЮЙУМП, ТБЪДЕМЕООПЕ ОБ 100.

рП ЙФПЗХ ЗТБЖЩ «чМЙСОЙЕ ЖБЛФПТПЧ» РПМХЮБЕФУС ОПМШ, Ф.Л. Ч ДБООПН ТБУЮЕФЕ ПРТЕДЕМЕОП ЧМЙСОЙЕ ЙЪНЕОЕОЙК ЧОХФТЕООЕК УФТХЛФХТЩ РПЛБЪБФЕМС ОБ ПВЭХА ЕЗП УХННХ. оЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ПРТЕДЕМСАФУС РП РПМПЦЙФЕМШОЩН ПФЛМПОЕОЙСН Ч УХННЕ ЪБФТБФ, Ф.Л. ПОЙ ПФТБЦБАФ РЕТЕТБУИПД. рП ТЕЪХМШФБФБН ТБУЮЕФПЧ ТБЪТБВБФЩЧБАФУС НЕТЩ РП ПРФЙНЙЪБГЙЙ ЪБФТБФ ч ЮБУФОПУФЙ, Ч РТЙЧЕДЕООПН РТЙНЕТЕ РЕТЕТБУИПД РП УФБФШЕ «уЩТШЕ Й НБФЕТЙБМЩ» ФТЕВХЕФ РЕТЕУНПФТБ ФЕИОПМПЗЙЙ РТПЙЪЧПДУФЧБ У ГЕМША ЙУРПМШЪПЧБОЙС ПФИПДПЧ НБФЕТЙБМПЧ, ХУЙМЕОЙС ЛПОФТПМС ЪБ ТБУИПДПЧБОЙЕН НБФЕТЙБМПЧ Ч РТПЙЪЧПДУФЧЕ Й Ф.Д.

рТЙНЕОЕОЙЕ ЛПОЛТЕФОПЗП НБФЕНБФЙЮЕУЛПЗП РТЙЕНБ ДПМЦОП ПРЙТБФШУС ОБ НЕФПДПМПЗЙА НБФЕНБФЙЮЕУЛПЗП НПДЕМЙТПЧБОЙС ЬЛПОПНЙЮЕУЛЙИ РТПГЕУУПЧ.

ч ЪБЧЙУЙНПУФЙ ПФ ЖПТН УЧСЪЙ НЕЦДХ ЙУУМЕДХЕНЩНЙ ЬЛПОПНЙЮЕУЛЙНЙ РПЛБЪБФЕМСНЙ ТЕЫЕОЙС ЪБДБЮ НПЗХФ ВЩФШ ФПЮОЩНЙ ЙМЙ РТЙВМЙЦЕООЩНЙ. еУМЙ ЖПТНБ УЧСЪЙ ДЕФЕТНЙОЙТПЧБООБС, ФП ЕУФШ ПВЯЕЛФЙЧОП ЧЪБЙНПУЧСЪБООЩ Й ЪБЧЙУЙНЩ ЙУУМЕДХЕНЩЕ РПЛБЪБФЕМЙ, ФП ТЕЪХМШФБФЩ ТБУЮЕФПЧ ВХДХФ ФПЮОЩНЙ. еУМЙ ЦЕ ЖПТНБ УЧСЪЙ УФПИБУФЙЮЕУЛБС, ФП ЕУФШ УМХЮБКОБС, ЧЕТПСФОПУФОБС, ФП ТЕЪХМШФБФЩ ТБУЮЕФПЧ РПМХЮБАФУС РТЙВМЙЦЕООЩНЙ. ьФП ФТЕВХЕФ ПФ БОБМЙФЙЛБ ОЕПВИПДЙНПУФЙ РПДФЧЕТЦДБФШ ЙМЙ РТПЧЕТСФШ ОБДЕЦОПУФШ РПМХЮЕООЩИ ТЕЪХМШФБФПЧ ТБУЮЕФПЧ, ХУФБОБЧМЙЧБФШ УФЕРЕОШ РПЗТЕЫОПУФЙ Ч ТБУЮЕФБИ У ГЕМША ЙИ ЛПТТЕЛФЙТПЧЛЙ. нОПЗЙЕ РТЙЕНЩ УФБФЙУФЙЛЙ Й НБФЕНБФЙЛЙ РТЕДХУНБФТЙЧБАФ УРЕГЙБМШОЩЕ УРПУПВЩ ЛПТТЕЛФЙТПЧЛЙ ТЕЪХМШФБФЙЧОПЗП РПЛБЪБФЕМС ОБ РПЗТЕЫОПУФШ Ч ТБУЮЕФБИ. чНЕУФЕ У ФЕН, УМЕДХЕФ ПФНЕФЙФШ, ЮФП ОЕ ЧУЕЗДБ ФТЕВХЕФУС ЧЩУПЛБС ФПЮОПУФШ Ч ЬЛПОПНЙЮЕУЛЙИ ТБУЮЕФБИ, РПЬФПНХ БОБМЙФЙЛЙ ПЗТБОЙЮЙЧБАФУС ТЕЪХМШФБФБНЙ ЧЩЮЙУМЕОЙК ВЕЪ ЛПТТЕЛФЙТПЧЛЙ ОБ РПЗТЕЫОПУФШ.

оБЙВПМЕЕ РПРХМСТОЩНЙ Ч ЬЛПОПНЙЛЕ СЧМСАФУС НЕФПДЩ ЛПТТЕМСГЙЙ Й ТЕЗТЕУУЙЙ, ТБУЮЕФЩ ДЙУРЕТУЙЙ, ТЕЦЕ ЙУРПМШЪХАФУС НЕФПДЩ ФТБОУРПТФОПК ЪБДБЮЙ, УЕФЕЧЩИ ЗТБЖЙЛПЧ, ФЕПТЙЙ ЙЗТ Й НБУУПЧПЗП ПВУМХЦЙЧБОЙС Й ДТ.

пУПВЕООПУФЙ ЙУРПМШЪПЧБОЙС Ч БОБМЙЪЕ НЕФПДПЧ ЛПТТЕМСГЙЙ Й ТЕЗТЕУУЙЙ ЪБЛМАЮБЕФУС Ч ФПН, ЮФП ПОЙ ПУОПЧБОЩ ОБ ЙЪХЮЕОЙЙ УЧСЪЙ НЕЦДХ РПЛБЪБФЕМЕН Й ЖБЛФПТБНЙ, ЙЪНЕТЕОЙЙ ЕЕ ФЕУОПФЩ Й УЙМЩ ЧМЙСОЙС. рПУЛПМШЛХ ДМС ПГЕОЛЙ ДЕСФЕМШОПУФЙ РТЕДРТЙСФЙС ЙУРПМШЪХЕФУС ВПМШЫПЕ ЛПМЙЮЕУФЧП УБНЩИ ТБЪОППВТБЪОЩИ РПЛБЪБФЕМЕК, ФП ОБ РЕТЧПН ЬФБРЕ ЙИ БОБМЙЪБ У РТЙНЕОЕОЙЕН ЛПТТЕМСГЙЙ Й ТЕЗТЕУУЙЙ ФТЕВХЕФУС ХУФБОПЧЙФШ ОБМЙЮЙЕ УЧСЪЙ Й ЕЕ ЖПТНХ У ЧПЪНПЦОЩНЙ ЖБЛФПТБНЙ.

еУМЙ НЕЦДХ РПЛБЪБФЕМЕН Й ЖБЛФПТБНЙ ХУФБОПЧМЕОБ ЖХОЛГЙПОБМШОБС УЧСЪШ, ПВХУМПЧМЕООБС НЕФПДЙЛПК ТБУЮЕФБ, ФП ФБЛБС УЧСЪШ ОБЪЩЧБЕФУС ДЕФЕТНЙОЙТПЧБООПК . ч ЬФПН УМХЮБЕ УФТПЙФУС ДЕФЕТНЙОЙТПЧБООБС НПДЕМШ ЪБЧЙУЙНПУФЙ РПЛБЪБФЕМС ПФ ЧЪБЙНПУЧСЪБООЩИ У ОЙН ЖБЛФПТПЧ. тБУЮЕФЩ ФБЛЙИ НПДЕМЕК ПУХЭЕУФЧМСАФУС Ч ПУОПЧОПН ФТБДЙГЙПООЩНЙ УРПУПВБНЙ Й ПУОПЧБОЩ ОБ ЬМЙНЙОЙТПЧБОЙЙ ЖБЛФПТПЧ.

еУМЙ НЕЦДХ РПЛБЪБФЕМЕН Й ЖБЛФПТБНЙ ПФУХФУФЧХЕФ ЖХОЛГЙПОБМШОБС УЧСЪШ, УМЕДПЧБФЕМШОП ПОБ ОПУЙФ УФПИБУФЙЮЕУЛЙК, УМХЮБКОЩК ИБТБЛФЕТ. юФПВЩ ХУФБОПЧЙФШ ОБМЙЮЙЕ, ФЕУОПФХ Й ИБТБЛФЕТ УЧСЪЙ ЧППВЭЕ, ЙУРПМШЪХАФУС НЕФПДЩ ЛПТТЕМСГЙЙ Й ТЕЗТЕУУЙЙ. йИ РТЙНЕОЕОЙЕ ЙНЕЕФ ОЕЛПФПТЩЕ ПЗТБОЙЮЕОЙС. рТЕЦДЕ ЧУЕЗП, ОХЦОБ ВПМШЫБС ЧЩВПТЛБ ДБООЩИ; ЮЕН ВПМШЫЕ ПОБ, ФЕН ФПЮОЕЕ ТБУЮЕФЩ. уПЧПЛХРОПУФШ ЧЩВПТЛЙ ДПМЦОБ ВЩФШ ПДОПТПДОПК Й ХУФПКЮЙЧПК. ьФП ЧБЦОП ДМС ПРТЕДЕМЕОЙС ЪБЛПОПНЕТОПУФЕК Ч ТБЪЧЙФЙЙ РПЛБЪБФЕМС Ч ЪБЧЙУЙНПУФЙ ПФ ЖБЛФПТПЧ Й ЙУЛМАЮЕОЙС ЪБЧЙУЙНПУФЙ ПФ УХВЯЕЛФЙЧОПЗП РПДИПДБ.

рПУФТПЕОЙЕ НБФЕНБФЙЮЕУЛПК НПДЕМЙ ЪБЧЙУЙФ ПФ ЛПМЙЮЕУФЧБ ЖБЛФПТПЧ. юБЭЕ ЧУЕЗП ЙУРПМШЪХАФУС ПДОПЖБЛФПТОЩЕ НПДЕМЙ, ЛПФПТЩЕ ВЩУФТП РТПУЮЙФЩЧБАФУС ВЕЪ РТЙНЕОЕОЙС ьчн, Б НОПЗПЖБЛФПТОЩЕ ФТЕВХАФ ЙУРПМШЪПЧБОЙС РТПЗТБНН Й ьчн. рП НОЕОЙА ПФДЕМШОЩИ ЬЛПОПНЙУФПЧ ГЕМЕУППВТЪОЕЕ ЙУРПМШЪПЧБФШ ПДОПЖБЛФПТОЩЕ НПДЕМЙ, Ф.Л. ЙИ ЧРПМОЕ ДПУФБФПЮОП ДМС ДПУФЙЦЕОЙС ГЕМЕК БОБМЙЪБ. пДОБЛП ТБЪЧЙФЙЕ ЛПНРМЕЛУОПЗП БОБМЙЪБ РТЕДРПМБЗБЕФ ОЕПВИПДЙНПУФШ ЙУРПМШЪПЧБОЙС НОПЗПЖБЛФПТОЩИ НПДЕМЕК, ЮФП Ч ЪОБЮЙФЕМШОПК НЕТЕ РПЧЩЫБЕФ ПВЯЕЛФЙЧОПУФШ ЧЩЧПДПЧ.

юФПВЩ РТБЧЙМШОП РПУФТПЙФШ НПДЕМШ Й ТЕЫЙФШ ЧПРТПУ П ГЕМЕУППВТБЪОПУФЙ ЕЕ ТБУЮЕФБ, ОЕПВИПДЙНП ОБ ХТПЧОЕ ЛПТТЕМСГЙПООПЗП БОБМЙЪБ ХУФБОПЧЙФШ ФЕУОПФХ УЧСЪЙ НЕЦДХ РПЛБЪБФЕМЕН Й ЖБЛФПТПН. у ЬФПК ГЕМША ТБУУЮЙФЩЧБЕФУС ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ РП ПДОПК ЙЪ ЖПТНХМ, РТЕДМБЗБЕНЩИ УФБФЙУФЙЛПК. еУМЙ ЕЗП ТБЪНЕТЩ ПФТБЦБАФ ЪБНЕФОХА УЧСЪШ, ФП РТПЧПДЙФУС ЪБФЕН Й ТЕЗТЕУУЙПООЩК БОБМЙЪ, РП ТЕЪХМШФБФБН ЛПФПТПЗП ХУФБОБЧМЙЧБЕФУС УФЕРЕОШ ЪБЧЙУЙНПУФЙ ЙЪНЕОЕОЙС РПЛБЪБФЕМС ПФ ЖБЛФПТПЧ.

уХЭОПУФШ ЛПТТЕМСГЙЙ ЪБЛМАЮБЕФУС Ч ФПН, ЮФП НЕЦДХ РПЛБЪБФЕМЕН Й УМХЮБКОП ЧЩВТБООЩН ЖБЛФПТПН ЙЪХЮБЕФУС ОБМЙЮЙЕ Й ФЕУОПФБ УЧСЪЙ. рПД ФЕУОПФПК УЧСЪЙ РПОЙНБЕФУС ЮБУФПФБ ЧМЙСОЙС ЖБЛФПТБ ОБ РПЛБЪБФЕМШ РТЙ ХУМПЧЙЙ ЕЗП ЙОДЙЧЙДХБМШОПЗП ЧМЙСОЙС Й ЙЪПМСГЙЙ ДТХЗЙИ ЖБЛФПТПЧ.

дМС ВПМЕЕ ФПЮОЩИ ТБУЮЕФПЧ ПЮЕОШ ЧБЦОП РТБЧЙМШОП РПДПВТБФШ ЮЙУМП ЧЩВПТЛЙ. пФДЕМШОЩЕ ЬЛПОПНЙУФЩ УЮЙФБАФ, ЮФП ЮЙУМП ЧЩВПТЛЙ ДПМЦОП ВЩФШ ОЕ НЕОЕЕ 20 — 25.

рТЙ ПГЕОЛЕ ДЙОБНЙЮЕУЛПЗП ТСДБ УФТПЙФУС ЗТБЖЙЛ, ОБ ЛПФПТПН ТБЪНЕЭЕОЙЕ y Й x (РПЛБЪБФЕМС Й ЖБЛФПТБ) РПЛБЦЕФ ИБТБЛФЕТ УЧСЪЙ. уЧСЪШ НПЦЕФ ВЩФШ РТСНПМЙОЕКОБС ЙМЙ ЛТЙЧПМЙОЕКОБС.

рТЙ РТСНПМЙОЕКОПК ЪБЧЙУЙНПУФЙ Ч ТБУЮЕФЕ ЙУРПМШЪХЕФУС МЙОЕКОЩК ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ, Б РТЙ ЛТЙЧПМЙОЕКОПК — ЛПТТЕМСГЙПООПЕ ПФОПЫЕОЙЕ. йУИПДОЩЕ ДБООЩЕ ЙЪ ФБВМЙГЩ 10, ОБОЕУЕООЩЕ ОБ ЗТБЖЙЛЕ 1, ПФТБЦБАФ МЙОЕКОХА УЧСЪШ, УМЕДПЧБФЕМШОП ДМС ЙЪНЕТЕОЙС ФЕУОПФЩ УЧСЪЙ ОЕПВИПДЙНП ЙУРПМШЪПЧБФШ МЙОЕКОЩК ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ.

чЩРХУЛ РТПДХЛГЙЙ
&nbsp	юЙУМЕООПУФШ ТБВПФОЙЛПЧ	&nbsp

зТБЖЙЛ 1 — ъБЧЙУЙНПУФШ НЕЦДХ ЧЩРХУЛПН РТПДХЛГЙЙ Й ЮЙУМЕООПУФША ТБВПФОЙЛПЧ.

R —	ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ;
—	ДЙУРЕТУЙС ЧЩВПТЛЙ ЪОБЮЕОЙК РПЛБЪБФЕМСС Й ЖБЛФПТБ;
—	ДЙУРЕТУЙС ЧЩВПТЛЙ ЖБЛФПТЙБМШОЩИ ЪОБЮЕОЙК;
—	ДЙУРЕТУЙС ЧЩВПТЛЙ ЪОБЮЕОЙК РПЛБЪБФЕМС;

, ЗДЕ &nbsp&nbsp&nbsp(2)

x — ЪОБЮЕОЙЕ ЖБЛФПТБ РП ЙОДЙЧЙДХБМШОПК ЧЩВПТЛЕ;

— УТЕДОЕЕ ЪОБЮЕОЙЕ ЖБЛФПТБ;

y — ЪОБЮЕОЙЕ РПЛБЪБФЕМС РП ЙОДЙЧЙДХБМШОПК ЧЩВПТЛЕ;

— УТЕДОЕЕ ЪОБЮЕОЙЕ РПЛБЪБФЕМС;

n — ЮЙУМП ЧЩВПТЛЙ;

&nbsp&nbsp&nbsp(3)

&nbsp&nbsp&nbsp(4)

ч ФБВМЙГЕ 10 РТЕДУФБЧМЕОЩ ЙУИПДОЩЕ ДБООЩЕ ЧЩВПТЛЙ РПЛБЪБФЕМС (y) ЧЩРХУЛБ РТПДХЛГЙЙ, ЖБЛФПТБ (x) ЮЙУМЕООПУФЙ ТБВПФОЙЛПЧ, Б ФБЛЦЕ ТБУЮЕФЩ ПФЛМПОЕОЙК ПФ ЙИ УТЕДОЙИ ЪОБЮЕОЙК Й ДТХЗЙИ РПЛБЪБФЕМЕК, ОЕПВИПДЙНЩИ ДМС ТБУЮЕФБ ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ, Б Ч ДБМШОЕКЫЕН Й ХТБЧОЕОЙС ТЕЗТЕУУЙЙ.

фБВМЙГБ 10 —

йУИПДОЩЕ ДБООЩЕ ДМС ЛПТТЕМСГЙПООП-ТЕЗТЕУУЙПООПЗП БОБМЙЪБ

(РЕТЙПДЩ) ЗПДЩ n	y — ЧЩР. РТПД.	x-ЮЙУМЕООПУФШ ТБВПФОЙЛПЧ						xy
1	12	3	— 4,8	23,04	-4,2	17,64	9	36	20,16
2	13	4	— 3,8	14,44	— 3,2	10,24	16	52	12,16
3	15	6	-1,8	3,24	-1,2	1,44	36	90	2,16
4	17	7	0,2	0,04	-0,2	0,04	49	119	0,04
Й Ф.Д.	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp	&nbsp
йФПЗП:	404	172	0	411,36	0	315,36	1548	3252	356,64

рПДУФБЧМСС ЪОБЮЕОЙС РПЛБЪБФЕМЕК Ч ЖПТНХМЩ (2), (3) Й (4), РПМХЮБЕН ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ РП РПЛБЪБФЕМА ЧЩРХУЛБ РТПДХЛГЙЙ 4,14, РП ЖБЛФПТХ — ЮЙУМЕООПУФЙ ТБВПФОЙЛПЧ 3,62, Й ЛЧБДТБФ ПФЛМПОЕОЙК ЪОБЮЕОЙК РПЛБЪБФЕМС Й ЖБЛФПТБ — 14,87. рПДУФБЧЙЧ Ч ЙИ ЖПТНХМХ (1), РПМХЮЙН ЛПЬЖЖЙГЙЕОФ ЛПТТЕМСГЙЙ л = 0,992.

ч УППФЧЕФУФЧЙЙ У ЛМБУУЙЖЙЛБГЙЕК ФЕУОПФЩ УЧСЪЙ НЕЦДХ ЖБЛФПТПН Й ТЕЪХМШФБФЙЧОЩН РТЙЪОБЛПН (РПЛБЪБФЕМЕН), РТЕДМБЗБЕНПК Ч ЬЛПОПНЙЮЕУЛПК МЙФЕТБФХТЕ, Ч ЙУУМЕДХЕНПН УМХЮБЕ УЧСЪШ ИБТБЛФЕТЙЪХЕФУС ЛБЛ ПЮЕОШ ФЕУОБС (ЧЩУПЛБС), ФБЛ ЛБЛ РТЕЧЩЫБЕФ РТЕДЕМ 0,9. рТЙ ЪОБЮЕОЙЙ ЛПЬЖЖЙГЙЕОФБ ЛПТТЕМСГЙЙ ПФ 0,7 ДП 0,9 УЧСЪШ ИБТБЛФЕТЙЪХЕФУС ЛБЛ ФЕУОБС, ПФ 0,5 ДП 0,7 — ЪБНЕФОБС, Б ДП 0,5 — УМБВБС. ч РПУМЕДОЕН УМХЮБЕ УЮЙФБЕФУС ОЕГЕМЕУППВТБЪОЩН РТЙЧПДЙФШ ТЕЗТЕУУЙПООЩК БОБМЙЪ, ФБЛ ЛБЛ (K_Д) ЛПЬЖЖЙГЙЕОФ ДЕФЕТНЙОБГЙЙ (л Д = R 2 &middot100%) УПУФБЧЙМ ВЩ 25%, УМЕДПЧБФЕМШОП МЙЫШ Ч 25% УМХЮБЕЧ ЙЪ 100 ЧПЪНПЦОП ЧПЪОПЛОПЧЕОЙЕ ЧЪБЙНПУЧСЪЙ НЕЦДХ ЙУУМЕДХЕНЩНЙ РТЙЪОБЛБНЙ (ЧЕМЙЮЙОБНЙ). ч РТЙЧЕДЕООПН РТЙНЕТЕ л Д УПУФБЧМСЕФ 0,992 2 = 0,98. уМЕДПЧБФЕМШОП Ч 98% УМХЮБЕЧ ЙЪ 100 ВХДЕФ РТПСЧМСФУС ЪБЧЙУЙНПУФШ ЧЩРХУЛБ РТПДХЛГЙЙ ПФ ЮЙУМЕООПУФЙ ТБВПФОЙЛПЧ. фБЛБС УЧСЪШ ИБТБЛФЕТЙЪХЕФУС ЛБЛ ЧЕУШНБ ФЕУОБС Й ДБЕФ ПУОПЧБОЙЕ РТПЧПДЙФШ ТЕЗТЕУУЙПООЩК БОБМЙЪ.

нЕФПД ТЕЗТЕУУЙЙ ПУОПЧЩЧБЕФУС ОБ РПУФТПЕОЙЙ НБФЕНБФЙЮЕУЛЙИ НПДЕМЕК ЪБЧЙУЙНПУФЙ РПЛБЪБФЕМЕК Й ЖБЛФПТПЧ.

нБФЕНБФЙЮЕУЛБС НПДЕМШ ПФТБЦБЕФ ДЕКУФЧЙФЕМШОПУФШ, Ф.Е. ИПЪСКУФЧЕООЩЕ РТПГЕУУЩ ОБ РТЕДРТЙСФЙСИ, Ч ПФТБУМЙ, Ч ТЕЗЙПОЕ Ч ЧЙДЕ НБФЕНБФЙЮЕУЛЙИ НПДЕМЕК Й ЖПТНХМ. оБРТЙНЕТ, Ч ТЕЗТЕУУЙПООПК НПДЕМЙ y = a + bx ЧЩТБЦБЕФУС РТСНПМЙОЕКОБС ЪБЧЙУЙНПУФШ НЕЦДХ РПЛБЪБФЕМЕН Й ЖБЛФПТПН. юБЭЕ ЧУЕЗП НПДЕМЙ УФТПСФУС РП ВПМЕЕ УМПЦОПК УИЕНЕ, Ф.Л. ПИЧБФЩЧБАФ ГЕМЩК ЛПНРМЕЛУ ЖБЛФПТПЧ, ЧМЙСАЭЙИ ОБ РПЛБЪБФЕМШ Й ЧЛМАЮЕООЩИ Ч БМЗПТЙФН ТБУЮЕФБ:

y — ЧЩРХУЛ РТПДХЛГЙЙ, x₁ — ЮЙУМЕООПУФШ ВТЙЗБДЩ 1, x₂ — РТПЙЪЧПДЙФЕМШОПУФШ ФТХДБ, Й Ф.Д.

жБЛФПТЩ, ЧЛМАЮБЕНЩЕ Ч БМЗПТЙФН ЪБЧЙУСФ ПФ УПДЕТЦБОЙС РПЛБЪБФЕМС, ПФ ГЕМЙ Й ЪБДБЮ БОБМЙЪБ Й Ф.Д.

ч ЬЛПОПНЙЛП-НБФЕНБФЙЮЕУЛПН НПДЕМЙТПЧБОЙЙ ЙУРПМШЪХАФУС ОЕУЛПМШЛП ФЙРПЧ НПДЕМЕК ЛБЛ РТПУФЩИ, ФБЛ Й УМПЦОЩИ (РПУФТПЕООЩИ ОБ ВПМЕЕ ЗМХВПЛЙИ ЧЪБЙНПУЧСЪСИ НЕЦДХ РПЛБЪБФЕМСНЙ Й ЖБЛФПТБНЙ).

уХЭЕУФЧХЕФ ОЕУЛПМШЛП ФЙРПЧ НПДЕМЕК:

1. бДДЙФЙЧОЩЕ — ПОЙ УФТПСФУС ОБ РТПУФПК УХННЕ ЖБЛФПТПЧ y = x₁ + x₂ + . + x_n. тБЪОПЧЙДОПУФСНЙ БДДЙФЙЧОЩИ НПДЕМЕК НПЗХФ ВЩФШ НПДЕМЙ ВБМБОУПЧПК ХЧСЪЛЙ, ЗДЕ ЛТПНЕ ЪОБЛБ «+» НПЦЕФ ВЩФШ «-«. тЕБМЙЪБГЙС = пУФ. ОБ ЛПОЕГ + рТЙИ. — рТ. ЧПР. — пУФ. ОБ ЛПОЕГy = x₁ + x₂ — x₃ — x₄
2. нХМШФЙРМЙЛБФЙЧОЩЕ НПДЕМЙ УФТПСФУС ОБ РТПЙЪЧЕДЕОЙЙ ЖБЛФПТПЧ y = x₁ &times x₂ &times x₃ &times x₄ ЙМЙ y = a₀ + a₁x₁ + a₂x₂ + . + a_nx_n. нХМШФЙРМЙЛБФЙЧОЩЕ НПДЕМЙ НПЗХФ ПФТБЦБФШ ЪБЧЙУЙНПУФШ ЧЩРХУЛБ РТПДХЛГЙЙ ПФ ЬЖЖЕЛФЙЧОПУФЙ ЙУРПМШЪПЧБОЙС ПУОПЧОЩИ ЖПОДПЧ, ЙИ БЧБОУЙТПЧБООПК УФПЙНПУФЙ Й ДТ. ч ЬФПН УМХЮБЕ НПДЕМШ ТБУЮЕФБ УФТПЙФУС РП БМЗПТЙФНХ: y = x₁ &times x₂
3. лТБФОЩЕ НПДЕМЙ, УФТПСФУС ОБ ДТПВСИ (ОБ ДЕМЕОЙЙ): тЕОФБВЕМШОПУФШ = рТЙВЩМШ/чЩТХЮЛБ, Ф.Е. y = x₁/x₂

лБЦДЩК ФЙР НПДЕМЙТПЧБОЙС РПДЧЕТЗБЕФУС ЛПТТЕЛФЙТПЧЛБН, ЛПФПТЩЕ ОБЪЩЧБАФУС НЕФПДБНЙ НПДЕМЙТПЧБОЙС. пОЙ ЪБЛМАЮБАФУС Ч ХДМЙОЕОЙЙ, ТБУЫЙТЕОЙЙ ЙМЙ УПЛТБЭЕОЙЙ РПУФТПЕООЩИ НПДЕМЕК. хДМЙОЕОЙЕ РТЕДХУНБФТЙЧБЕФ УМПЦЕОЙЕ УМБЗБЕНЩИ, Ф.Е. ЖБЛФПТПЧ НПДЕМЕК. уПЛТБЭЕОЙЕ РТЕДХУНБФТЙЧБЕФ ДЕМЕОЙЕ ЛБЦДПЗП ЙЪ ЬМЕНЕОФПЧ БМЗПТЙФНБ ОБ ПДОП Й ФПЦЕ ЮЙУМП.

ч ЪБЧЙУЙНПУФЙ ПФ ЖПТНЩ УЧСЪЙ Й ЕЕ ФЕУОПФЩ РПДВЙТБЕФУС ХТБЧОЕОЙЕ ТЕЗТЕУУЙЙ ЙМЙ НБФЕНБФЙЮЕУЛБС НПДЕМШ, ЛПФПТБС НПЦЕФ ЙНЕФШ ЧЙД РТЙ ПДОПЖБЛФПТОПК ЪБЧЙУЙНПУФЙ:

y = a + bx (РТСНПМЙОЕКОБС ЪБЧЙУЙНПУФШ),

y = a + b/x (ЛТЙЧПМЙОЕКОБС),

ЗДЕ y — РПЛБЪБФЕМШ,

a — РПУФПСООЩК РБТБНЕФТ РТСНПК, ЛПФПТЩК ПФТБЦБЕФ ОЕЙЪНЕООХА (ОЕЪБЧЙУЙНХА) ЮБУФШ РПЛБЪБФЕМС ПФ ЖБЛФПТБ Й РПЛБЪЩЧБЕФ ЧЩУПФХ РТСНПК ОБД ПУША БВУГЙУУ,

b — ЙНЕЕФ ЬЛПОПНЙЮЕУЛЙК УНЩУМ Й РПЛБЪЩЧБЕФ ЧП УЛПМШЛП ТБЪ ЙЪНЕОЙФУС РПЛБЪБФЕМШ «Х» У ЙЪНЕОЕОЙЕН ЖБЛФПТБ «И» ОБ ЕДЙОЙГХ.

дМС ТЕЫЕОЙС ХТБЧОЕОЙС РТСНПМЙОЕКОПК ЪБЧЙУЙНПУФЙ y = a + bx ЙУРПМШЪХЕФУС УЙУФЕНБ ОПТНБМШОЩИ ХТБЧОЕОЙК:

ЛБЦДПЕ ЙЪ ХТБЧОЕОЙК ДЕМЙФУС ОБ ЛПЬЖЖЙГЙЕОФ РТЙ «Б». дБМЕЕ ЙЪ РЕТЧПЗП ХТБЧОЕОЙС ЧЩЮЙФБЕФУС 2-ПЕ Й ТБУУЮЙФЩЧБЕФУС ЪОБЮЕОЙЕ РБТБНЕФТБ «b». ч ОБЫЕН РТЙНЕТЕ РП ДБООЩН ФБВМЙГЩ 10 РПДВЙТБЕН ЮЙУМПЧЩЕ ЪОБЮЕОЙС Ч УЙУФЕНХ ОПТНБМШОЩИ ХТБЧОЕОЙК:

рПУМЕ ДЕМЕОЙС ЛБЦДПЗП ЙЪ ХТБЧОЕОЙК ОБ ЛПЬЖЖЙГЙЕОФ РТЙ РБТБНЕФТЕ «Б», ЙЪ РЕТЧПЗП ХТБЧОЕОЙС ЧЩЮЙФБЕН ЧФПТПЕ:

рПДУФБЧЙЧ ЪОБЮЕОЙС ТБУУЮЙФБООЩИ РБТБНЕФТПЧ «Б» Й «b» РПМХЮЙН ТЕЫЕООХА ТЕЗТЕУУЙПООХА НБФЕНБФЙЮЕУЛХА НПДЕМШ:

Y x = 8,727 + 1,131x

ьЛПОПНЙЮЕУЛЙК УНЩУМ ЕЈ ЪБЛМАЮБЕФУС Ч ФПН, ЮФП У ЙЪНЕОЕОЙЕН ЖБЛФПТБ «x» — ЮЙУМЕООПУФЙ ТБВПФОЙЛПЧ — ОБ 1, ЧЩРХУЛ РТПДХЛГЙЙ ВХДЕФ, УППФЧЕФУФЧЕООП, ТБУФЙ ЙМЙ УОЙЦБФШУС Ч 0,957 ТБЪ. ч ТЕЪХМШФБФЕ РТЕДУФБЧМСЕФУС ЧПЪНПЦОЩН ЧЩЮЙУМЙФШ РТПЗОПЪ ЙЪНЕОЕОЙК ЧЩРХУЛБ РТПДХЛГЙЙ РТЙ РМБОПЧПН (РТПЗОПЪЙТХЕНПН) ЪОБЮЕОЙЙ ЮЙУМЕООПУФЙ ФТХДБ. еУМЙ ЪБ УЮЕФ НПДЕТОЙЪБГЙЙ Й ТБУЫЙТЕОЙС РТПЙЪЧПДУФЧБ РТЕДРТЙСФЙЕ ХЧЕМЙЮЙФ ЮЙУМЕООПУФШ ТБВПФОЙЛПЧ ДП 20, ФП ЧЩРХУЛ РТПДХЛГЙЙ РТЙ РТПЮЙИ ТБЧОЩИ ХУМПЧЙСИ НПЦЕФ УПУФБЧЙФШ 29,1.

фБЛЙН ПВТБЪПН, ЛПТТЕМСГЙПООП-ТЕЗТЕУУПООЩК НЕФПД БОБМЙЪБ НПЦЕФ ЫЙТПЛП ЙУРПМШЪПЧБФШУС РТЙ РМБОЙТПЧБОЙЙ Й РТПЗОПЪЙТПЧБОЙЙ ПУОПЧОЩИ РПЛБЪБФЕМЕК ДЕСФЕМШОПУФЙ РТЕДРТЙСФЙС.

нЕФПД ЧБТЙБГЙЙ ПУОПЧЩЧБЕФУС ОБ ЙЪНЕТЕОЙЙ ЛПМЕВБОЙК ЖБЛФЙЮЕУЛПЗП ЪОБЮЕОЙС РПЛБЪБФЕМС Ч РПМПЦЙФЕМШОХА ЙМЙ ПФТЙГБФЕМШОХА УФПТПОХ ПФ УТБЧОЙЧБЕНПК ЧЕМЙЮЙОЩ. юБЭЕ ЧУЕЗП ЬФПФ НЕФПД ЙУРПМШЪХЕФУС Ч ТБУЮЕФБИ ЛПЬЖЖЙГЙЕОФПЧ ТЙФНЙЮОПУФЙ Й ТБЧОПНЕТОПУФЙ. рПД ТЙФНЙЮОПУФША РПОЙНБЕФУС ЙУУМЕДПЧБОЙЕ РПЛБЪБФЕМС ЧП ЧТЕНЕОЙ, Б РПД ТБЧОПНЕТОПУФША — Ч РТПУФТБОУФЧЕ. тБУЮЕФ ЧЛМАЮБЕФ ПРТЕДЕМЕОЙЕ ЛПЬЖЖЙГЙЕОФПЧ ТЙФНЙЮОПУФЙ, ЧБТЙБГЙЙ (ДЙУРЕТУЙЙ) Й ЛЧБДТБФЙЮЕУЛПЗП ПФЛМПОЕОЙС. лЧБДТБФ ПФЛМПОЕОЙК РПЪЧПМСЕФ ЙЪВБЧЙФШУС ПФ ЪОБЛПЧ Й ВПМЕЕ ФПЮОП ПРТЕДЕМЙФШ ЬФЙ ПФЛМПОЕОЙС. лПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ РПЛБЪЩЧБЕФ УФЕРЕОШ ОЕТЙФНЙЮОПУФЙ Й, РП УХФЙ, ПФТБЦБЕФ ПФОПУЙФЕМШОЩК ТБЪНЕТ ОЕЙУРПМШЪПЧБООЩИ ТЕЪЕТЧПЧ. пО ЙУРПМШЪХЕФУС ДМС ТБУЮЕФБ РПФЕОГЙБМШОПЗП ТЕЪЕТЧБ, Ч ЛПФПТПН ХЮЙФЩЧБАФУС ЧПЪНПЦОПУФЙ РТЕДРТЙСФЙС ОЕ ФПМШЛП ДПУФЙЗБФШ ПРФЙНБМШОПЗП ТБЪНЕТБ РПЛБЪБФЕМС РМБОБ, ОП Й ЕЗП РПФЕОГЙБМШОЩЕ ЧПЪНПЦОПУФЙ РЕТЕЧЩРПМОСФШ ЬФЙ ЪБДБОЙС.

рП ТБУУЮЙФБООЩН ЛПЬЖЖЙГЙЕОФБН ТЙФНЙЮОПУФЙ ДБЕФУС ПГЕОЛБ ЬЖЖЕЛФЙЧОПУФЙ ПТЗБОЙЪБГЙЙ РТПЙЪЧПДУФЧБ. рТЙ ЬФПН УТБЧОЕОЙЕ ЖБЛФЙЮЕУЛПЗП ЪОБЮЕОЙС ЛПЬЖЖЙГЙЕОФБ ТЙФНЙЮОПУФЙ ДЕМБЕФУС У РМБОПЧЩН, ЕУМЙ ПО ХУФБОБЧМЙЧБЕФУС , Б ФБЛЦЕ УП УТЕДОЕПФТБУМЕЧЩН ЪОБЮЕОЙЕН Й Ф.Д.

лПЬЖЖЙГЙЕОФ ТЙФНЙЮОПУФЙ (ТБЧОПНЕТОПУФЙ) ЧЛМАЮБЕФ УЙУФЕНХ ЖПТНХМ:

K_Т — ЛПЬЖЖЙГЙЕОФ ТЙФНЙЮОПУФЙ (ТБЧОПНЕТОПУФЙ)

V — ЛПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ

, ЗДЕ

— ЛЧБДТБФЙЮЕУЛПЕ ПФЛМПОЕОЙЕ РПЛБЪБФЕМС ПФ ЕЗП УТЕДОЕЗП ЪОБЮЕОЙС

(3), ЗДЕ

И — ЪОБЮЕОЙС ЙУУМЕДХЕНЩИ РПЛБЪБФЕМЕК

— ЙИ УТЕДОЕЕ ЪОБЮЕОЙЕ

n — ЮЙУМП ЧЩВПТЛЙ

ч ТСДЕ УМХЮБЕЧ, Ч ЮБУФОПУФЙ Ч ТБУЮЕФБИ ЛПЬЖЖЙГЙЕОФБ ТБЧОПНЕТОПУФЙ, НПЗХФ ЙУРПМШЪПЧБФШУС ТБУЮЕФЩ ЧЪЧЕЫЕООЩИ ЛЧБДТБФЙЮЕУЛЙИ ПФОПЫЕОЙК:

, ЗДЕ

f — ЪОБЮЕОЙЕ ЗТХРРЙТПЧПЮОПЗП РТЙЪОБЛБ Ч ТБУЮЕФБИ

жПТНХМБ ЧЪЧЕЫЕООПК ДЙУРЕТУЙЙ РТЙНЕОСЕФУС, ЕУМЙ ЧЩВПТЛБ ДБООЩИ ДЕМБЕФУС РП РТЕДРТЙСФЙСН, РП ЧЙДБН РТПДХЛГЙЙ Й Ф.Д. ч ЬФПН УМХЮБЕ ЙНЕЕФ НЕУФП ЗТХРРЙТПЧЛБ РПЛБЪБФЕМЕК Й ЮЙУМП ЧЩВПТПЛ Ч ЛБЦДПК ЗТХРРЕ. фБЛЙН ПВТБЪПН «f» РТЕДУФБЧМСЕФ УПВПК ЛПМЙЮЕУФЧП РТЕДРТЙСФЙК ЙМЙ РТПДХЛГЙЙ Ч РПДЗТХРРЕ ЧЩВПТЛЙ.

дБООЩЕ ДМС ТБУЮЕФБ ЛПЬЖЖЙГЙЕОФПЧ ТЙФНЙЮОПУФЙ У ЙУРПМШЪПЧБОЙЕН ЛПЬЖЖЙГЙЕОФБ ЧБТЙБГЙЙ РТЙЧЕДЕОЩ Ч ФБВМЙГЕ 11.

фБВМЙГБ 11 —

дБООЩЕ П ЧЩРХУЛЕ РТПДХЛГЙЙ РП ДЕЛБДБН ПФЮЕФОПЗП РЕТЙПДБ

дЕЛБДЩ НЕУСГБ	рМБО	жБЛФЙЮЕУЛЙ	% ЧЩРПМОЕОЙС РМБОБ			пФЛМПОЕОЙЕ РМБОБ
1	325	339	104,3	+2,7	7,29	+14
2	340	336	98,8	-2,8	7,84	-4
3	345	351	101,7	+0,1	0,01	+6
йФПЗП	1010	1026	101,6	И	15,14	+16

ъБ РТЙОЙНБЕФУС УТЕДОЙК РТПГЕОФ ЧЩРПМОЕОЙС РМБОБ ЧЩРХУЛБ РТПДХЛГЙЙ ЪБ ПФЮЕФОЩК РЕТЙПД ЛПФПТЩК УПУФБЧЙМ 101,6.

рПДУФБЧЙЧ ЪОБЮЕОЙС РПЛБЪБФЕМЕК Ч ЖПТНХМЩ 1,2,3, РПМХЮЙН:

л_ТЙФН = 100 — 2,2 = 97,8

фБЛЙН ПВТБЪПН Ч ПФЮЕФОПН РЕТЙПДЕ ЧЩРХУЛ РТПДХЛГЙЙ ПУХЭЕУФЧМСМУС ДПУФБФПЮОП ТЙФНЙЮОП, ЕУМЙ ХЮЕУФШ, ЮФП УТЕДОЕПФТБУМЕЧПК РПЛБЪБФЕМШ УПУФБЧМСЕФ 97%. фЕН ОЕ НЕОЕЕ ОЕЙУРПМШЪПЧБООЩЕ ТЕЪЕТЧЩ ЙНЕМЙ НЕУФП. йИ ТЕЛПНЕОДХЕФУС ТБУУЮЙФЩЧБФШ ДЧХНС УРПУПВБНЙ:

1. ТЕБМШОЩК ТЕЪЕТЧ, ЛПФПТЩК ПФТБЦБЕФ УХННХ ОЕДПЧЩРПМОЕОЙС РМБОБ ЧЩРХУЛБ РТПДХЛГЙЙ Ч ПФЮЕФОПН РЕТЙПДЕ. ч РТЙЧЕДЕООПН РТЙНЕТЕ (ФБВМЙГБ 11) ЬФПФ ТЕЪЕТЧ УПУФБЧЙМ 4 Ф.Т. Ч ТЕЪХМШФБФЕ ОЕЧЩРПМОЕОЙС РМБОБ ЧП ЧФПТПК ДЕЛБДЕ;
2. РПФЕОГЙБМШОЩК ТЕЪЕТЧ, ПФТБЦБАЭЙК ЧПЪНПЦОПУФЙ РТЕДРТЙСФЙС ХДЕТЦЙЧБФШ ДПУФЙЗОХФЩК ХТПЧЕОШ РТПЙЪЧПДУФЧБ РТЙ ХУМПЧЙЙ, ЮФП ПО ЧЩЫЕ 100%. ч РТЙЧЕДЕООПН РТЙНЕТЕ УТЕДОЙЕ ЧПЪНПЦОПУФЙ РТЕДРТЙСФЙС Ч ЧЩРХУЛЕ РТПДХЛГЙЙ УПУФБЧМСАФ РТЕЧЩЫЕОЙЕ РМБОПЧЩИ ЪБДБОЙК ОБ 1,6% (101,6 — 100). пФУАДБ РПФЕОГЙБМШОЩК ТЕЪЕТЧ УПУФБЧЙФ:

(ЖБЛФЙЮЕУЛЙК ПВЯЕН РТПЙЪЧПДУФЧБ РТПДХЛГЙЙ &times ЛПЬЖЖЙГЙЕОФ ЧБТЙБГЙЙ)/100 = (1026 &times 2,2)/100 = 22,6 Ф.Т.

1. дБФШ ИБТБЛФЕТЙУФЙЛХ ФТБДЙГЙПООЩИ Й ЬЛПОПНЙЛП-НБФЕНБФЙЮЕУЛЙИ НЕФПДПЧ ЬЛПОПНЙЮЕУЛПЗП БОБМЙЪБ Й ЧПЪНПЦОПУФЙ ЙИ РТБЛФЙЮЕУЛПЗП ЙУРПМШЪПЧБОЙС.
2. дБФШ ИБТБЛФЕТЙУФЙЛХ ДПУФПЙОУФЧ Й ОЕДПУФБФЛПЧ ЛПТТЕЛФЙТПЧЛЙ Й ГЕРОЩИ РПДУФБОПЧПЛ.
3. дБФШ ИБТБЛФЕТЙУФЙЛХ УПДЕТЦБОЙС Й УЖЕТЩ РТЙНЕОЕОЙС РТЙЕНПЧ ВБМБОУПЧПК ХЧСЪЛЙ Й ПФЛМПОЕОЙК.
4. дБФШ ИБТБЛФЕТЙУФЙЛХ ДПУФПЙОУФЧ Й ОЕДПУФБФЛПЧ ЙОДЕЛУОПЗП Й ЙОФЕЗТБМШОПЗП РТЙЕНПЧ.
5. ч ЮЕН УПУФПЙФ УРЕГЙЖЙЛБ РТЙЕНБ РТПГЕОФОЩИ ЮЙУЕМ Й УЖЕТЩ ЕЗП РТЙНЕОЕОЙС Ч ЬЛПОПНЙЮЕУЛПН БОБМЙЪЕ?
6. ч ЮЕН ЪБЛМАЮБЕФУС УХЭОПУФШ РТЙЕНБ ЛПТТЕМСГЙЙ Й ЛБЛЙЕ ФТЕВПЧБОЙС РТЕДЯСЧМСАФУС Л ХУМПЧЙСН ЕЗП РТЙНЕОЕОЙС?
7. лБЛЙН ПВТБЪПН ЙУРПМШЪХЕФУС Ч ЬЛПОПНЙЮЕУЛПН БОБМЙЪЕ РТЙЕН ТЕЗТЕУУЙЙ?
8. дБФШ ИБТБЛФЕТЙУФЙЛХ РТЙЕНБ ЧБТЙБГЙЙ Й ЕЗП ЧПЪНПЦОПУФЕК Ч ПГЕОЛЕ ТБЧОПНЕТОПУФЙ Й ТЙФНЙЮОПУФЙ ИПЪСКУФЧЕООЩИ РТПГЕУУПЧ.

&nbsp&nbsp&nbsp&nbsp

Источник