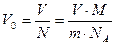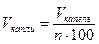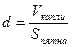Способ оценки размеров молекул

Способ оценки размеров молекул

«Физика — 10 класс»

Какие физические объекты (системы) изучает молекулярная физика?
Как различить механические и тепловые явления?

В основе молекулярно-кинетической теории строения вещества лежат три утверждения:

1) вещество состоит из частиц;
2) эти частицы беспорядочно движутся;
3) частицы взаимодействуют друг с другом.

Каждое утверждение строго доказано с помощью опытов.

Свойства и поведение всех без исключения тел определяются движением взаимодействующих друг с другом частиц: молекул, атомов или ещё более малых образований — элементарных частиц.

Оценка размеров молекул. Для полной уверенности в существовании молекул надо определить их размеры. Проще всего это сделать, наблюдая расплывание капельки масла, например оливкового, по поверхности воды. Масло никогда не займёт всю поверхность, если мы возьмём достаточно широкий сосуд (рис. 8.1). Нельзя заставить капельку объёмом 1 мм 2 расплыться так, чтобы она заняла площадь поверхности более 0,6 м 2 . Предположим, что при растекании масла по максимальной площади оно образует слой толщиной всего лишь в одну молекулу — «мономолекулярный слой». Толщину этого слоя нетрудно определить и тем самым оценить размеры молекулы оливкового масла.

Объём V слоя масла равен произведению его площади поверхности S на толщину d слоя, т. е. V = Sd. Следовательно, линейный размер молекулы оливкового масла равен:

Современные приборы позволяют увидеть и даже измерить отдельные атомы и молекулы. На рисунке 8.2 показана микрофотография поверхности кремниевой пластины, где бугорки — это отдельные атомы кремния. Подобные изображения впервые научились получать в 1981 г. с помощью сложных туннельных микроскопов.

Размеры молекул, в том числе и оливкового масла, больше размеров атомов. Диаметр любого атома примерно равен 10 -8 см. Эти размеры так малы, что их трудно себе представить. В таких случаях прибегают к помощи сравнений.

Вот одно из них. Если пальцы сжать в кулак и увеличить его до размеров земного шара, то атом при том же увеличении станет размером с кулак.

Число молекул.

При очень малых размерах молекул число их в любом макроскопическом теле огромно. Подсчитаем примерное число молекул в капле воды массой 1 г и, следовательно, объёмом 1 см 3 .

Диаметр молекулы воды равен примерно 3 • 10 -8 см. Считая, что каждая молекула воды при плотной упаковке молекул занимает объём (3 • 10 -8 см) 3 , можно найти число молекул в капле, разделив объём капли (1 см 3 ) на объём, приходящийся на одну молекулу:

Масса молекул.

Массы отдельных молекул и атомов очень малы. Мы вычислили, что в 1 г воды содержится 3,7 • 10 22 молекул. Следовательно, масса одной молекулы воды (Н₂0) равна:

Массу такого же порядка имеют молекулы других веществ, исключая огромные молекулы органических веществ; например, белки имеют массу, в сотни тысяч раз большую, чем масса отдельных атомов. Но всё равно их массы в макроскопических масштабах (граммах и килограммах) чрезвычайно малы.

Относительная молекулярная масса.

Так как массы молекул очень малы, удобно использовать в расчётах не абсолютные значения масс, а относительные.

По международному соглашению массы всех атомов и молекул сравнивают с массы атома углерода (так называемая углеродная шкала атомных масс).

Относительной молекулярной (или атомной) массой М_r вещества называют отношение массы m₀ молекулы (или атома) данного вещества к массы атома углерода:

Относительные атомные массы всех химических элементов точ- но измерены. Складывая относительные атомные массы элементов, входящих в состав молекулы вещества, можно вычислить относительную молекулярную массу вещества. Например, относительная молекулярная масса углекислого газа СO₂ приближённо равна 44, так как относительная атомная масса углерода практически равна 12, а кислорода примерно 16 : 12 + 2 • 16 = 44.

Сравнение атомов и молекул с массы атома углерода было принято в 1961 г. Главная причина такого выбора состоит в том, что углерод входит в огромное число различных химических соединений. Множитель введён для того, чтобы относительные массы атомов были близки к целым числам.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Основные положения МКТ. Тепловые явления — Физика, учебник для 10 класса — Класс!ная физика

Источник

Учебники

Журнал «Квант»

Общие

Кикоин А.К. Простой способ определения размеров молекул // Квант. — 1983. — № 9. — C.29-30.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

В молекулярной физике главные «действующие лица» — это молекулы, невообразимо маленькие частицы, из которых состоят все на свете вещества. Ясно, что для изучения многих явлений важно знать, каковы они, молекулы. В частности каковы их размеры.

Когда говорят о молекулах, их обычно считают маленькими упругими твердыми шариками. Следовательно, знать размер молекул значит знать их радиус.

Несмотря на малость молекулярных размеров, физики сумели разработать множество способов их определения. В «Физике 9» рассказывается о двух из них. В одном используется свойство некоторых (очень немногих) жидкостей растекаться в виде пленки толщиной в одну молекулу. В другом размер частицы определяется с помощью сложного прибора — ионного проектора.

Существует, однако, очень простой, хотя и не самый точный, способ вычисления радиусов молекул (или атомов) Он основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.

Число молекул в теле массой m равно, как известно, \(

N_a \frac\), где М — молярная масса вещества N_A — число Авогадро. Отсюда объем V₀ одной молекулы определяется из равенства

В это выражение входит отношение объема вещества к его массе. Обратное же отношение \(

\frac = \rho\) есть плотность вещества, так что

Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.

Объем одной молекулы, если считать ее шариком, равен \(

\frac<4> <3>\pi r^3\), где r — радиус шарика. Поэтому

откуда мы и получаем выражение для радиуса молекулы:

Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10 -9 моль 1/3 , поэтому формула для r ринимает вид

Например, радиус молекулы воды, вычисленный по этой формуле, равен r_В ≈ 1,9 · 10 -10 м.

Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул- шариков были бы невозможны молекулярные движения. Тем не менее вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.

Источник

Методы определения размеров молекул

В молекулярной физике главные «действующие лица» — это молекулы, невообразимо маленькие частицы, из которых состоят все на свете вещества. Ясно, что для изучения многих явлений важно знать, каковы они, молекулы. В частности, каковы их размеры.

Когда говорят о молекулах, их обычно считают маленькими упругими твердыми шариками. Следовательно, знать размер молекул, значит знать их радиус или диаметр.

Несмотря на малость молекулярных размеров, физики сумели разработать множество способов их определения. В одном используется свойство некоторых (очень немногих) жидкостей растекаться в виде пленки толщиной в одну молекулу. Вдругом, размер частицы определяется с помощью сложного прибора – ионного проектора.

Строение молекул изучают различными экспериментальными методами. Электронография, нейтронография и рентгеновский структурный анализ позволяют получать непосредственную информацию о структуре молекул. Электронографии, метод, исследующий рассеяние электронов на пучке молекул в газовой фазе, позволяет рассчитать параметры геометрической конфигурации для изолированных сравнительно простых молекул. Нейтронография и рентгеновский структурный анализ ограничены анализом структуры молекул либо отдельных упорядоченных фрагментов в конденсированной фазе. Рентгенографические исследования кроме указанных сведений дают возможность получить количественные данные о пространственном распределении электронной плотности в молекулах.

Спектроскопические методы основаны на индивидуальности спектров химических соединений, которая обусловлена характерным для каждой молекулы набором состояний и отвечающих им энергетических уровней. Эти методы позволяют проводить качественный и количественный спектральный анализ веществ.

Разнообразную информацию о строении и свойствах молекул дает изучение их поведения во внешних электрических и магнитных полях.

Существуют, однако, очень простые способы определения размеров молекул:

1 способ. Основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.

Число молекул в теле массой m равно, как известно, 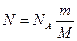, где М — молярная масса вещества N_A — число Авогадро. Отсюда объем V₀ одной молекулы определяется из равенства

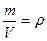
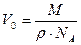
В это выражение входит отношение объема вещества к его массе. Обратное же отношение есть плотность вещества, так что .

Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.

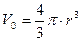
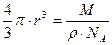
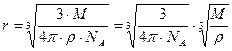
Объем одной молекулы, если считать ее шариком, равен , где r — радиус шарика. Поэтому , откуда мы и получаем выражение для радиуса молекулы:

.

Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10 -9 моль 1/3 , поэтому формула для r принимает вид .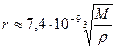

Например, радиус молекулы воды, вычисленный по этой формуле, равен r_В ≈ 1,9 · 10 -10 м.

Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул – шариков были бы невозможны молекулярные движения. Тем не менее, вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.

2 способ. Метод Ленгмюра и Дево. В данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. При попадании капли раствора на поверхность воды спирт растворяется в воде, а исследуемая жидкость образует пятно площадью S и толщиной d (порядка диаметра молекул).

Если допустить, что молекула имеет форму шара, то объем одной молекулы равен:

где d – молекулы.

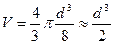
Необходимо определить диаметр молекулы d. В микропипетку набрать 0,5 мл раствора и, расположив ее над сосудом, отсчитать число капель n, содержащихся в этом объеме. Проделав опыт несколько раз, найти среднее значение числа капель в объеме 0,5 мл, а затем подсчитать объём исследуемой жидкости в капле: 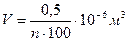, где n – число капель в объеме 0,5 мл, 1:400 – концентрация раствора.

В ванну налить воду толщиной 1 – 2 см. Насыпать тальк тонким слоем на лист бумаги, ударяя слегка пальцем по коробочке. Расположив лист бумаги выше и сбоку от ванны на расстоянии 10 – 20 см, тальк сдуть с бумаги. На поверхность воды в ванне из пипетки капнуть одну каплю раствора. Линейкой измерить, средний диаметр образовавшегося пятна D и подсчитываю его площадь. Опыт повторить 2- 3 раза, а затем подсчитать диаметр молекул d.

3 способ. Определение диаметра молекулы. Будем считать, что капля масла растекается по воде до тех пор, пока толщина масляной плёнки не станет равной одной молекуле, тогда диаметр одной молекулы можно определить по формуле: d=V/S, где V – объём капли масла, S — площадь масленого пятна. Объём капли масла можно определить следующим образом: накапать 100 капель из капилляра в сосуд и измерить массу масла в нём. После этого массу, выраженную в килограммах, поделить на плотность масла, которую можно взять из таблицы плотности некоторых веществ (плотность масла растительного 800 кг/м 3 ). Затем полученный результат поделить на количество капель. Объём капли можно определить также с помощью мерного цилиндра: накапать масло в цилиндр, измерить его объём в см 3 и перевести в м 3 , для чего поделить на 1000000, затем на количество капель масла. После того, как объём капли стал известен нужно капнуть одну каплю масла на поверхность воды, которая налита в широкий сосуд. Для ускорения реакции предварительно немного нужно нагреть воду – приблизительно до 40 0 С. Масло начнёт растекаться, и в результате получится круглое пятно. После того, как пятно перестанет расширяться, с помощью линейки измерить его диаметр и рассчитать площадь пятна по формуле: .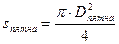

Ход эксперимента:

1. Определение объёма капли растительного масла.

В мерный цилиндр (мензурку) накапать 190 капель масла и определить объём их. Используя формулу для определения объёма1 капли масла из метода Ленгмюра и Дево (2 способ), рассчитать объем капли.

2. Определение площади масляного пятна.

Для того, чтобы получить масляное пятно провести несколько экспериментов.

В ванну размером 40×30 см необходимо налить воду и капнуть 1 каплю растительного масла, а затем наблюдать, как расплывается пятно, когда оно перестанет расплываться – измерить его диаметр.

№	Условия проведения эксперимента	Что увидели	Диаметр пятна (D, см)
1	В ванну налили холодную воду
2	Воду нагрели до 40 0 С и на поверхность насыпали тальк (измельчённый мел)
3	Воду нагрели до 40 0 С и добавили перманганат калия.

Для определения площади пятна использовать формулу: .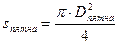

3. Определение диаметра молекулы растительного масла.

Используем формулу:

Источник