Методика оценки достоверности показателей
Под достоверностью статистических показателей следует понимать степень их соответствия отображаемой ими действительности.
Оценить достоверностьрезультатов исследования означает определить с какой вероятностью прогноза возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность.
В большинстве случаев врачу приходится, как правило, иметь дело с выборочной статистической совокупностью, а выводы по результатам такого исследования переносить на все явления в целом, т.е. на генеральную совокупность.
Мерой достоверности средней величины является средняя ошибка средней арифметической / mM /, которая находится в прямой зависимости от разнообразия признака / σ /ив обратной зависимости от числа наблюдений и находится по формуле:

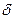
n – число наблюдений
Чтобы перенести полученные данные на генеральную совокупность, необходимо определить доверительные границы средних величин.
Мген. = Мвыб.± tmм , где t — доверительный коэффициент.
Величина критерия «t» связана определенными отношениями с вероятностью безошибочного прогноза — Р и численностью наблюдений в выборочной совокупности.
Зависимость доверительного критерия t от степени вероятности безошибочного прогноза Р /при п >30/ ( табл. 4):
| Степень вероятности безошибочного прогноза, Р в процентах | Доверительный критерий t |
| 95,0 | |
| 99,0 |
Для большинства медико-биологических и социальных исследований достоверными считаются доверительные границы, установленные с вероятностью безошибочного прогноза Р=95% и более. Чтобы найти критерий t при n
Проведем оценку достоверности по результатам определения среднего возраста врачей-инфекционистов:
Поэтапная оценка достоверности: 1. Определение средней ошибки / mM /
2. Определение доверительных границ при t = 2
Mmin = 44,l — 2,8 = 41,3 г.
Вывод: установлено с 95 % вероятностью безошибочного прогноза, что средний возраст врачей в генеральной совокупности варьирует от 41,3 г. до 46,9 г.
Методика оценки достоверности относительных величин
Оценка достоверности относительных величин проходит также в два этапа:
1.Определение средней ошибки для показателя / mp / по формуле:
где Р — показатель,
q — обратная величина показателю, если показатель выражен в процентах = 100 — Р; если в промиллях, то 1000 — Р и т.д. n — число наблюдений.
2. Определение доверительных границ для показателей
Р ген. = Рвыб. ± tmp
Р max. = Р выб. + tmp
Р min. = Р выб. – tmp
Вероятность безошибочного прогноза /95%/ будет при t = 2.
Пример: Изучались 1500 случаев брюшного тифа. Нашли, что кишечное кровотечение наблюдалось в 300 случаях. Определить процент кишечного кровотечения у больных (Р) и в каких пределах возможна вероятная ошибка? / при t = 2/
Рген. = 20,0 ± 2 х 1,03
Рmах. = 20,0 + 2,06 =22,06%
Pmin.= 20,0 — 2,06=17,94%
Вывод: установлено с 95% вероятностью прогноза, что кишечные кровотечения у больных брюшным тифом в генеральной совокупности наблюдаются не чаще, чем в 22,06% и не реже, чем в 17,94% случаев.
Методика оценки достоверности разности результатов
Исследования
Оценить достоверность разности результатов исследования означает решить вопрос, является ли различие показателей /средних величин/ существенным, обусловленным действием разных факторов или вызвано случайными колебаниями.
При числе наблюдений более 30 достоверность разности средних величин определяется путем расчета критерия t по формуле:
Достоверность разности относительных показателей определяется по формуле:
где M1 и М2 — средняя арифметическая
P1 и Р2 — показатели сравниваемых совокупностей,
m1 и m2 — соответствующие ошибки.
Полученный критерий t оценивается по общепринятым правилам:
если t ≥ 2, то разность следует считать достоверной, т.е. она соответствует вероятности безошибочного прогноза, равной 95% и более /Р ≥ 95%/. Если же t 
Пример: Определить, существенно ли отличаются средние величины пульса у 50 больных пневмонией и у 50 здоровых /контрольная группа/.
| Исследуемые контингенты | Пульс | М /средняя арифметическая/ | m /ошибка/ |
| Здоровые | ±10 | ||
| Больные | ±12 |
При t = 2,1 вероятность Р > 95%. Следовательно, наблюдаемое различие в числе пульсовых ударов у больных и здоровых не случайно, а достоверно, существенно.
Пример: Определить эффективность лечения тетрациклином при рожистом воспалении по сравнению с лечением пенициллином:
Сравнение результатов лечения пенициллином и тетрациклином больных рожистым воспалением.
| Вид антибиотика | Число больных | Имели рецидивы | абс.число | проценты |
| Пенициллин | ±15,0 | |
| Тетрациклин | ±7,6 |
1 .Вычисляем ошибки /m/ для каждого показателя:


Последнее изменение этой страницы: 2017-05-05; Просмотров: 1108; Нарушение авторского права страницы
Источник
Цель занятия
на основе применения метода оценки достоверности результатов исследования уметь перенести результаты выборочного исследования общественного здоровья, деятельности врачей и учреждений здравоохранения на генеральную совокупность.
Студент должен уметь
— определять достоверность результатов исследования с помощью ошибки репрезентативности интенсивного показателя и средней величины;
— определять доверительные границы средних и относительных вели-
— определять достоверность разности между двумя средними величинами, относительными показателями;
— выбирать способ оценки достоверности результатов исследования при решении ситуационной задачи, определять достоверность и делать соответствующие выводы.
Студент должен знать:
— определение «достоверность результатов исследования»;
— параметрические и непараметрические способы оценки достоверности результатов исследования;
— условия применения параметрического и непараметрических способов оценки достоверности результатов исследования;
— определение ошибки репрезентативности средней величины и интенсивного показателя, ее вычисление;
— понятие о критерии «t», его выбор в способе определения доверительных границ и оценку в способе достоверности разности результатов исследования.
Место проведения: аудитория кафедры общественного здоровья и организации здравоохранения с курсом медицинской информатики, дисплейный класс.
Мультимедийный проектор Ноутбук
Наглядный материал в виде мультимедийной презентации Персональный компьютер
Информационный материал
В практической и научно-практической работе врачи обобщают результаты, полученные как правило на выборочных совокупностях. Для более широкого распространения и применения, полученных при изучении репрезентативной выборочной совокупности данных и выводов надо уметь по части явления судить о явлении и его закономерностях в целом.
Учитывая, что врачи, как правило, проводят исследования на выборочных совокупностях, теория статистики позволяет с помощью математического аппарата (формул) переносить данные с выборочного исследования на генеральную совокупность. При этом врач должен уметь не только воспользоваться математической формулой, но сделать вывод, соответствующий каждому способу оценки достоверности полученных данных. С этой целью врач должен знать способы оценки достоверности.
Применяя метод оценки достоверности результатов исследования для изучения общественного здоровья и деятельности учреждений здравоохранения, а также в своей научной деятельности, исследователь должен уметь правильно выбрать способ данного метода. Среди методов оценки достоверности различают параметрические и непараметрические.
Параметрические методы оценки достоверности
называют количественные методы статистической обработки данных, применение которых требует обязательного знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Непараметрические методы оценки достоверности
являются количественные методы статистической обработки данных, применение которых не требует знания закона распределения изучаемых признаков в совокупности и вычисления их основных параметров.
Как параметрические, так и непараметрические методы, используемые для сравнения результатов исследований, т.е. для сравнения выборочных совокупностей, заключаются в применении определенных формул и расчете определенных показателей в соответствии с предписанными алгоритмами. В конечном результате высчитывается определенная числовая величина, которую сравнивают с табличными пороговыми значениями. Критерием достоверности будет результат сравнения полученной величины и табличного значения при данном числе наблюдений (или степеней свободы) и при заданном уровне безошибочного прогноза.
Таким образом, в статистической процедуре оценки основное значение имеет полученный критерий достоверности, поэтому сам способ оценки дос-
товерности в целом иногда называют тем или иным критерием по фамилии автора, предложившего его в качестве основы метода.
Применение параметрических методов
При проведении выборочных исследований полученный результат не обязательно совпадает с результатом, который мог бы быть получен при исследовании всей генеральной совокупности. Между этими величинами существует определенная разница, называемая ошибкой репрезентативности, т.е. это погрешность, обусловленная переносом результатов выборочного исследования на всю генеральную совокупность.
Ошибка репрезентативности
Средняя ошибка средней
где σ — среднеквадра-
арифметической величины опреде-
ляется по формуле:
n — число наблюдений
Ошибка относительного пока-
где p — показатель, вы-
зателя определяется по формуле:
раженный в %, ‰, %оо и т.д.
q = (100 — р), при p выраженном
или (1000 — р), при p выражен-
или (10000 — р), при p выра-
женном в %оо и т.д.
При числе наблюдений меньше 30 ошибки репрезентативности определяются соответственно по формулам:
Определение доверительных границ средних и относительных величин
Формулы определения доверительных границ представлены следующим образом:
для средних величин (М): М ген = М выб ± tm
для относительных показателей (Р): Р ген = Р выб ± tm
где М ген и Р ген — соответственно, значения средней величины и относительного показателя генеральной совокупности;
М вы6 и Р вы6 — значения средней величины и относительного показателя выборочной совокупности;
m — ошибка репрезентативности;
t — критерий достоверности (доверительный коэффициент).
Данный способ применяется в тех случаях, когда по результатам выборочной совокупности необходимо судить о размерах изучаемого явления (или признака) в генеральной совокупности.
Обязательным условием для применения способа является репрезентативность выборочной совокупности. Для переноса результатов, полученных при выборочных исследованиях, на генеральную совокупность необходима степень вероятности безошибочного прогноза (Р), показывающая, в каком
проценте случаев результаты выборочных исследований по изучаемому признаку (явлению) будут иметь место в генеральной совокупности.
При определении доверительных границ средней величины или относительного показателя генеральной совокупности, исследователь сам задает определенную (необходимую) степень вероятности безошибочного прогноза
Для большинства медико-биологических исследований считается достаточной степень вероятности безошибочного прогноза, равная 95%, а число случаев генеральной совокупности, в котором могут наблюдаться отклонения от закономерностей, установленных при выборочном исследовании, не будут превышать 5%. При ряде исследований, связанных, например, с применением высокотоксичных веществ, вакцин, оперативного лечения и т.п., в результате чего возможны тяжелые заболевания, осложнения, летальные исходы, применяется степень вероятности Р = 99,7%, т.е. не более чем у 1% случаев генеральной совокупности возможны отклонения от закономерностей, установленных в выборочной совокупности.
Заданной степени вероятности (Р) безошибочного прогноза соответствует определенное, подставляемое в формулу, значение критерия t, зависящее также и от числа наблюдений.
При n>30 степени вероятности безошибочного прогноза Р = 99,7% — соответствует значение t = 3, а при Р = 95,5% — значение t = 2.
При п ген ) при числе наблюдений больше 30
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у 36 обследованных водителей сельскохозяйственных машин через 1 ч работы составила 80 ударов в 1 минуту; σ = ± 6 ударов в минуту.
Задание: определить ошибку репрезентативности (m M ) и доверительные границы средней величины генеральной совокупности (М ген ).
1. Вычисление средней ошибки средней арифметической (ошибки репрезентативности) (m):
m = σ / √n = 6 / √36 = ±1 удар в минуту
2. Вычисление доверительных границ средней величины генераль-
ной совокупности (М ген ). Для этого необходимо:
o а) задать степень вероятности безошибочного прогноза (Р = 95
o б) определить величину критерия t. При заданной степени вероятности (Р=95%) и числе наблюдений меньше 30 величина критерия t, опре-
деляемого по таблице, равна 2 (t = 2). Тогда М ген = М выб ± tm = 80 ± 2×1 = 80 ± 2 удара в минуту.
Вывод. Установлено с вероятностью безошибочного прогноза Р = 95%, что средняя частота пульса в генеральной совокупности, т.е. у всех водителей сельскохозяйственных машин, через 1 ч работы в аналогичных условиях будет находиться в пределах от 78 до 82 ударов в минуту, т.е. средняя частота пульса менее 78 и более 82 ударов в минуту возможна не более, чем у 5% случаев генеральной совокупности.
на определение ошибок репрезентативности (m) и доверительных границ относительного показателя генеральной совокупности (Р ген )
Условие задачи: при медицинском осмотре 164 детей 3 летнего возраста, проживающих в одном из районов городе Н., в 18% случаев обнаружено нарушение осанки функционального характера.
Задание: определить ошибку репрезентативности (m p ) и доверительные границы относительного показателя генеральной совокупности (Р ген ).
1. Вычисление ошибки репрезентативности относительного
m = √P x q / n = √18 x (100 — 18) / 164 = ± 3%
2. Вычисление доверительных границ средней величины генеральной совокупности (Р ген ) производится следующим образом:
o необходимо задать степень вероятности безошибочного прогноза (Р=95%);
o при заданной степени вероятности и числе наблюдений больше 30, величина критерия t равна 2 (t = 2). Тогда Р ген =
Р выб ± tm = 18% ± 2 х 3 = 18% ± 6%.
Вывод. Установлено с вероятностью безошибочного прогноза Р=95%, что частота нарушения осанки функционального характера у детей 3 летнего возраста, проживающих в городе Н., будет находиться в пределах от 12 до 24% случаев.
Оценка достоверности разности результатов исследования
Данный способ применяется в тех случаях, когда необходимо определить, случайны или достоверны (существенны), т.е. обусловлены какой-то причиной, различия между двумя средними величинами или относительными показателями.
Обязательным условием для применения данного способа является репрезентативность выборочных совокупностей, а также наличие причинноследственной связи между сравниваемыми величинами (показателями) и факторами, влияющими на них.
Формулы определения достоверности разности представлены следующим образом:
для средних величин
для относительных показателей
где t — критерий достоверности, m 1 и m 2 — ошибки репрезентативности, М 1 и М 2 — средние величины, Р 1 и Р 2 — относительные показатели.
Если вычисленный критерий t более или равен 2 (t ≥ 2), что соответствует вероятности безошибочного прогноза Р равном или более 95% (Р ≥ 95%), то разность следует считать достоверной (существенной), т.е. обусловленной влиянием какого-то фактора, что будет иметь место и в генеральной совокупности.
При t Поэтому полученный критерий должен всегда оцениваться по от-
ношению к конкретной цели исследования.
на оценку достоверности разности средних величин
Условие задачи: при изучении комбинированного воздействия шума и низкочастотной вибрации на организм человека было установлено, что средняя частота пульса у водителей сельскохозяйственных машин через 1 ч после начала работы составила 80 ударов в минуту; m = ± 1 удар в мин. Средняя частота пульса у этой же группы водителей до начала работы равнялась 75 ударам в минуту; m = ± 1 удар в минуту.
Задание: оценить достоверность различий средних значений пульса у водителей сельскохозяйственных машин до и после 1 ч работы.
Вывод. Значение критерия t = 3,5 соответствует вероятности безошибочного прогноза Р > 99,7%, следовательно можно утверждать, что различия в средних значениях пульса у водителей сельскохозяйственных машин до и после 1 ч работы не случайно, а достоверно, существенно, т.е. обусловлено влиянием воздействия шума и низкочастотной вибрации.
на оценку достоверности разности относительных показателей
Условие задачи: при медицинском осмотре детей 3 летнего возраста в 18% (m = ± 3%) случаях обнаружено нарушение осанки функционального характера. Частота аналогичных нарушений осанки при медосмотре детей 4- летнего возраста составила 24% (m = ± 2,64%).
Источник