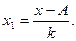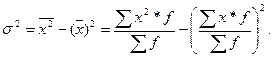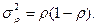Метод моментов
Содержание:
- Примеры с решением
| Метод моментов |
Метод моментов, предложенный английским статистиком Карлом Пирсоном в 1894 г., заключается в приравнивании определенного числа выборочных моментов к соответствующим теоретическим, которые являются функциями неизвестных параметров 
Рассматривая количество моментов, равное числу к неизвестных параметров, подлежащих определению, и решая полученные уравнения относительно этих параметров, получаем искомые оценки. Иначе говоря, оценки параметров 
являются решениями систем уравнений 
или 
, для некоторых 
Метод моментов содержит неопределенность, поскольку можно получить уравнения для неизвестных параметров 
, используя как начальные, так и центральные моменты, а также некоторые их модификации типа асимметрии или эксцесса.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Пример:
Функция
задает плотность распределения Рэлея (см. § 6.4). Требуется оценить параметр 
по выборке 
Найдем оценку параметра 0, приравнивая начальные выборочные и теоретические моменты. Первый начальный момент
имеет вид: 
Приравнивая, получаем первую оценку параметра: 
Приравнивая вторые начальные моменты, можем получить другую оценку: 
из уравнения, которое получитсяся при использовании второго центрального момента (дисперсии), — третью оценку: 
- Часто полагают, что для нахождения оценки одного параметра следует брать первый момент, для двух — первые два момента и т.п. По возможности действительно имеет смысл поступать так, поскольку это проще всего. Однако такой подход годится не всегда. Он не проходит, например, если некоторые моменты равны нулю или не зависят от нужных параметров.
В общем случае система уравнений для моментов может не иметь решения в элементарных функциях (и тогда можно искать решение приближенными методами) или вообще оказаться неразрешимой (несовместной).
Оценки, полученные методом моментов, часто оказываются смешенными. К достоинствам метода моментов следует отнести его простую вычислительную реализацию, а также то, что оценки являются функциями от выборочных моментов.
В силу теоремы Слуцкого любая непрерывная функция от выборочных моментов функции сходится по вероятности к постоянной, получаемой подстановкой в эту функцию теоретических моментов, если они существуют и если получаемая таким образом постоянная конечна. Для определенности рассмотрим функцию 
от двух моментов (начальных или центральных), хотя ее можно обобщить на любое конечное число аргументов, в том числе и на случай, когда Н зависит только от одного аргумента.
Теорема 1. (Крамера). Пусть в некоторой окрестности точки 
функция 
непрерывна и имеет непрерывные частные производные первого и второго порядка:
Тогда для любой выборки, по которой найдены оценки 
, случайная величина 
асимптотически нормальна при 
следующими параметрами:
Иногда оценки, получаемые с помощью метода моментов, принимаются в качестве первого приближения, по которому можно построить другими методами оценки более высокого качества.
Оценки метода моментов используются также, когда существует необходимость оценить не сами параметры распределения (которые часто представляют собой некие абстракции), а определенные практически значимые показатели, зависящие от этих параметров функционально: 
. Самый простой (хотя и не самый точный) способ такого оценивания — подставить полученные оценки в соответствующую функцию: 
Если распределение определяется одним параметром, то для построения оценки один теоретический момент приравнивают к одному эмпирическому моменту того же порядка (обычно первого).
Возможно вам будут полезны данные страницы:
Источник
Моменты распределения
Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.
Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.
Первое свойство заключается в том, что если из всех вариант вычесть какое-то постоянное число, то дисперсия от этого не изменится. Оно позволяет рассчитывать дисперсию не по отклонениям вариант от средней (часто имеющей дробное значение), а по отклонениям от целого числа. Второе свойство позволяет все варианты разделить на какое-то постоянное число, например на значение интервала, и исчислить дисперсию уменьшенных вариант, а полученную величину умножить на квадрат этого числа.
, 
.
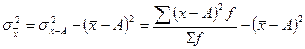
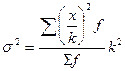
где: s 2 x – дисперсия отклонений вариантов от средней арифметической;
– дисперсия отклонений вариантов от произвольной величины А.
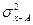
1. На этих свойствах основан расчет дисперсии способом отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х1=(х – А)/k, и последующем расчете дисперсии по формуле:
способ отсчета от условного нуля: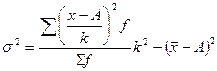 
;
способ моментов: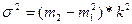 
, где
условный момент первого порядка: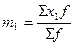 
;
условный момент второго порядка: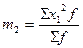 
, 
2. Дисперсия равна среднему квадрату значений признака за вычетом квадрата среднего значения признака:
Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.
В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком. Например, доля междугородных телефонных соединений (разговоров), предоставленных с ожиданием до 1 часа. Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака. Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда
Естественно, средняя постоянная величины р есть сама эта величина, а дисперсия равна: 
Средняя и дисперсия это частные случаи более широкого понятия обобщающих характеристик любого распределения моментов.
Момент распределения – это средняя арифметическая тех или иных степеней отклонений вариантов х от некоторой постоянной величины А:
mz =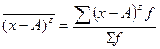 
.
Порядок момента определяется величиной z, т.е. степенью, в которую возводится отклонение вариант. В зависимости от принятой величины А различают три вида моментов:
начальные (при А=0):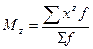 
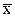
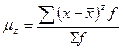
; центральные (при А=
): 
;
условные (при А≠0, А≠):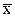 
.
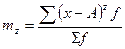
Начальный момент первого порядка представляет собой среднюю арифметическую: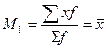 
;
центральный момент второго порядка – дисперсию: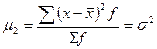 
. Центральный момент первого порядка m1 всегда равен нулю (сумма отклонений вариант от средней равна нулю); центральный момент третьего порядка равен нулю в симметричном распределении.
Условные моменты самостоятельного значения не имеют, ими пользуются для упрощения вычисления центральных моментов: m2 = m2 – m 2 1; m3 = m3 – 3m1 m2 + 2m 3 1; m4 = m4 – 4m3 m1 + 6m2 m 2 1 – 3 m 4 1.
Для исчисления условных моментов используется условная величина:
; ; 
; 
; где
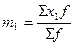
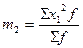
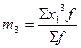
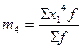
В этом случае центральные моменты корректируются на величину k z :
Наряду с изучением вариации признака по всей совокупности в целом часто возникает необходимость проследить количественные изменения признака по группам, на которые разбита вся совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:
.
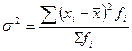
Межгрупповая дисперсияхарактеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:
, где
— соответственно средние и численности по отдельным группам,
— средняя всей совокупности.
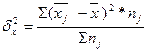
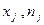
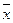
Внутригрупповая дисперсияотражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:
, где
— варианты групп, 
— численность группы, 
— средняя группы
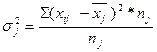
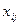
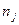
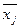
Средняя из внутригрупповых дисперсийопределяется по формуле:
.
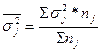
Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:
.
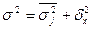
Данная сумма называется правилом сложения дисперсий.
Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.
На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результирующим признаками. Он называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:
.
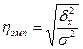
Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминациии показывает долю группировочного признака в общей вариации:
.
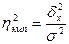
Источник
