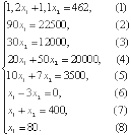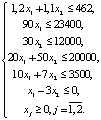Способ оптимизации экономико математических методов

Способ оптимизации экономико математических методов

Использование математических методов способствовало зарождению экономической науки. Применение математики к экономике обеспечило исследование и объяснение изменения спроса и предложения, рыночного равновесия, построения производственной функции и т.д. Математика на макроуровне обеспечивает решение задач выбора монетарной политики, формирования антициклической политики, прогнозирования экономического роста, занятости, объемов внешней торговли и изменения мировых рынков. На микроуровне математика решает задачи оценки и предсказания изменения спроса, предложения, поведения потребителей, оказывающихся под влиянием различных факторов, но наибольшую ценность математика несет в ее применении в организации производства. Вопрос выбора направления хозяйственной деятельности является наиболее важным для предприятия, поскольку оно всегда стремится максимизировать прибыль, а следовательно, снизить затраты и увеличить выручку. Данной цели можно достичь, применяя математические инструменты в поиске оптимальной производственной политики, обеспечивающей максимальную прибыль [1, с. 936].

Целью исследования является изучение практики применения экономико-математических методов в решении задачи оптимизации производственных процессов, снижения затрат и максимизации прибыли.

Объектом исследования выступают производственно-экономические отношения, возникающие в процессе планирования хозяйственной деятельности, оптимизации производственных процессов, сокращения затрат и максимизации прибыли хозяйствующих субъектов.

Материалы и методы исследования

В исследовании производилась оптимизация производства двух видов напитков с использованием графического метода линейного программирования, также рассматривался случай его применения для целочисленного линейного программирования. Наглядная интерпретация исходных и полученных в ходе работы данных была произведена в табличной и графической форме.

Материалы исследования были сформированы на основе работ отечественных и зарубежных ученых, опубликованных в ведущих рецензируемых изданиях из перечней ВАК и включаемых в международные базы данных, а также на основе учебно-методических работ.

Результаты исследования и их обсуждение

Рассмотрим простой, но реальный экономический процесс. Например, имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Сырье следует подбирать таким образом, чтобы оно использовалось и для одного, и для другого продуктов, в данном случае общими ресурсами являются вода, сахар и дрожжи. Также возможны случаи использования определенного сырья только для одного из конечных продуктов производства: так, для пива требуется солодовый, а для кваса – хлебный концентрат.

Следующий момент, на который нужно обратить внимание, – это количественные данные, т.е. расходы исходных продуктов на 1 л продукции и суточные запасы (табл. 1).

Исходные данные модели (начальное условие)

Кроме требований к запасам сырья, могут предъявляться и иные. Например, в связи с проведением чемпионата мира по футболу суточный спрос на пиво превышает спрос на квас, однако не более чем в 3 раза. Кроме того, установлено, что спрос на пиво не превышает 80 л за сутки. Для упаковки продукции фирма использует пластиковые бутылки объемом 1 л и в день может использовать не более 400 бутылок.

Обычно бывают два основных вопроса: составить оптимальный план производства продукции либо с наибольшей прибылью, либо с наименьшими затратами. Выбираем наибольшую прибыль, однако не хватает данных о цене продукции, значит, их следует добавить [2, с. 45].

Розничная цена за 1 л пива составляет 100 рублей, за 1 л кваса – 50 рублей. Целью экономико-математической задачи является найти количество пива и кваса, которое должна производить фирма, чтобы прибыль от реализации была наибольшей.

При введении переменных нужно отталкиваться от вопроса задачи, поэтому за x1 и x2 примем соответственно количество пива и кваса, выпускаемое фирмой в сутки, выраженное в литрах, значит, по смыслу задачи x1 ≥ 0, x2 ≥ 0. Для изготовления напитков требуется определенное соотношение ресурсов, а также нужно учесть, что потребление ресурсов не может превышать их запасов, значит, определены первые условия системы ограничений: .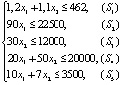

Здесь используются ресурсы: S1 – вода, S2 – солодовый концентрат, S3 – хлебный концентрат, S4 – сахар, S5 – дрожжи.

Далее нужно перевести оставшиеся дополнительные условия о суточной разнице спроса на напитки, об ограничениях в количестве 400 бутылок и в количестве пива 80 л, т.е. дописать условия x1 – 3×2 ≤ 0, x1 + x2 ≤ 400 и x1 ≤ 80. Эти неравенства соответствуют ресурсам: S6 – разница суточных спросов пива и кваса, S7 – количество используемых бутылок, S8 – спрос на пиво в сутки.

Целевая функция – это прибыль от реализации продаж, значит, F = 100×1 + 50×2 → max.

Задачи линейного программирования характеризуются некоторыми общими чертами. В каждой из них элементы решения представляют собой ряд неотрицательных переменных. Требуется также выбрать значения этих переменных, чтобы: выполнялись некоторые ограничения, имеющие вид линейных неравенств или неравенств относительно переменных; некоторая линейная функция F тех же переменных обращалась в максимум (минимум) [3, с. 11]. Полученная математическая модель производства относится к классу задач линейного программирования: найти F = 100×1 + 50×2 → max при системе ограничений .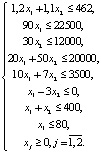

Используя алгоритм графического метода, необходимо:

1) построить область допустимых реше- ний;

2) отметить вектор 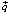, который проходит через точки (0;0) и (c1; c2), где c1 и c2 – коэффициенты при переменных в целевой функции. При определении максимума целевой функции направление вектора будет от точки (0;0) к точке (c1; c2), а при определении минимума – от точки (c1; c2) к точке (0;0);

3) изобразить линию уровня, проходящую через начало координат, т.е. прямую c1∙x1 + c2∙x2 = 0;

4) линию уровня переместить в направлении вектора 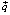. Перемещение линии уровня производится до тех пор, пока у нее не окажется только одна общая точка с областью допустимых решений. Эта точка определяет единственное решение задачи линейного программирования и будет точкой экстремума.

Границы области допустимых решений находятся из системы ограничений путем замены знаков неравенств равенствами, т.е.

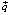
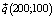
Вектор будет направлен от начала координат к точке (100; 50), однако в целях удобства масштаба рисунка можно удвоить координаты, получив в итоге .

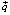
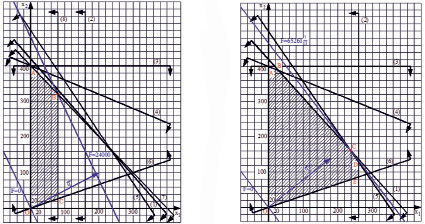
Линия уровня F = 0 или 100×1 + + 50×2 = 0 перемещается в направлении вектора до тех пор, пока линия уровня и область допустимых решений не будут иметь одну общую точку (на рис. 1(а) эта точка В). При этом значение целевой функции в этой точке равно Fmax = F(80, 320) = 24000.

Рис. 1. Нахождение оптимального решения графическим методом для начального условия (а) и измененного условия (б)

Подводя итог, можно отметить, что графическим способом был найден оптимальный план производства, а именно: если фирма будет производить за сутки 80 литровых бутылок пива и 320 литровых бутылок кваса, то можно получить наибольшую прибыль от продаж в размере 24 тыс. руб.

При решении многих экономических задач приходится рассматривать величины, принимающие только целые значения в силу своего экономического содержания. Подобные задачи относятся к задачам целочисленного линейного программирования [4].

Поскольку в результате решения задачи уже получилось решение x1 = 80, x2 = 320, то для целочисленного линейного программирования изменим условия. Запасы солодового концентрата равны 23 400 г, отсутствуют условия о том, что спрос на пиво не превышает 80 л за сутки и в день может использоваться не более 400 бутылок. Розничная цена за 1 л пива составит 180 рублей, за 1 л кваса – 140 рублей. Изменение условий задачи повлияет на составление математической модели. Теперь необходимо найти F = 180×1 + 140×2 → max при системе ограничений

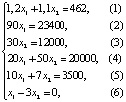
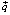
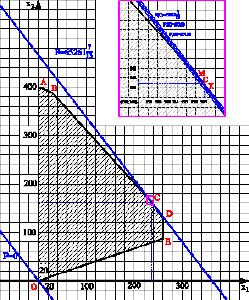
Границы области допустимых решений также изменяются в соответствии с новой системой, т.е. , а вектор будет направлен от начала координат к точке (180;140).

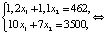
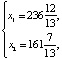
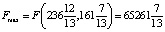
По рис. 1(б) точка оптимума – это точка С пересечения прямых (1) и (5); поскольку по графику видно, что она имеет нецелочисленные значения по осям координат, то найти координаты точки С можно, решив систему а целевая функция примет значение .

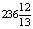
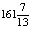
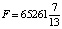
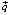
Как видно из решения, фирме необходимо выпустить литровых бутылок пива и бутылок кваса. Сделать это, конечно, не получится, поэтому требуется целочисленный ответ. Не всегда округление до целого значения в меньшую сторону обоих чисел дает наибольшую возможную прибыль, это зависит от соотношений сырья и его запасов, прибыли от продаж обоих напитков и иного, поэтому для нахождения целочисленного оптимума нужно увеличить часть рисунка возле точки С так, чтобы видна была каждая точка с целыми координатами в этой области. Линию уровня двигаем в направлении, обратном направлению вектора , до тех пор, пока не найдем первую целочисленную точку. Если есть сомнения в нескольких точках, можно их координаты подставить в целевую функцию и выбрать среди полученных значений наибольшее (рис. 2) [5].

Рис. 2. Нахождение оптимального решения графическим методом для целочисленного программирования

Определим значения целевой функции для точек X(237;161) и M(236;162), эти точки принадлежат области допустимых решений системы ограничений и являются ближайшими к точке оптимума С: F(X) = 180∙237 + 140∙161 = 65200; F(M) = 180∙236+140∙162 = 65160. Тогда Fmax цел = F(237, 161) = 65200.

Перейдем к анализу полученных решений. На рис. 1(а) и 1(б) можно увидеть, что не все прямые являются контурами границы области допустимых решений. Так, на рис. 1(а) область ограничена только прямыми (6), (7) и (8), а также осями координат, следовательно, условия системы ограничений, соответствующие прямым (1), (2), (3), (4) и (5), являются избыточными. На рис. 1(б) лишним является условие о ресурсе «хлебный концентрат», т.е. условие, соответствующее прямой (3). Все это говорит о том, что имелись неточности в определении ограничений.

На этом этапе нужно еще раз вернуться к началу и убрать лишние неравенства или скорректировать ограничения. Задача считается качественной, если каждое условие образует одну из сторон многоугольника решений. Если, например, сдвинуть некоторые прямые или изменить их наклон, то они уже будут давать новые стороны области решений. Таким образом, можно уменьшить либо количество неравенств в системе, либо запасы, пропорции и т.д.

Создадим итоговое условие задачи. Имеется фирма, которая выпускает 2 вида напитков: пиво и квас. Для изготовления пива используются 4 исходных продукта: вода, солодовый концентрат, сахар, дрожжи. Для изготовления кваса используются 4 исходных продукта: вода, хлебный концентрат, сахар, дрожжи. Расходы исходных продуктов на 1 л продукции и суточные запасы приведены в табл. 2.

Источник

Экономико-математические методы оптимизации производственной программы предприятия (развитие производственной мощности)

Содержание:

Предмет:	Экономика предприятия
Тип работы:	Реферат
Язык:	Русский
Дата добавления:	11.08.2019

• Данный тип работы не является научным трудом, не является готовой работой!
• Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.

Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!

По этой ссылке вы сможете найти рефераты по экономике предприятия на любые темы и посмотреть как они написаны:

Посмотрите похожие темы возможно они вам могут быть полезны:

Введение:

Экономико-математические методы (ЭММ) — это обобщенное название комплекса экономических и математических научных дисциплин, объединенных для изучения экономики.

Развитие современного общества характеризуется повышением технического уровня, усложнением организационной структуры производства, углублением общественного разделения труда и предъявлением высоких требований к методам планирования и управления экономикой. В этих условиях только научный подход к управлению экономической жизнью общества обеспечит высокие темпы развития народного хозяйства.

Одним из необходимых условий дальнейшего развития экономической науки является применение точных методов количественного анализа, широкое использование математики. В настоящее время последние достижения математики и современных компьютерных технологий находят более широкое применение в экономических исследованиях и планировании. Этому способствует развитие таких областей математики, как математическое программирование, теория игр, теория массового обслуживания, а также быстрое развитие высокоскоростной технологии электронных вычислений. Уже накоплен достаточный опыт в формулировании и решении экономических задач с использованием математических методов. Особенно успешно разработаны методы оптимального планирования, которые являются сущностью математического программирования.

Одной из основных задач является создание единой системы оптимального планирования и управления народным хозяйством, основанной на широком распространении в экономике математических методов и технологий электронных вычислений.

Производственная система как объект экономико-математического моделирования

Производственная система — это особый класс систем, которые являются частью производственного процесса, который изолирован в результате общественного разделения труда и способен производить продукты или предоставлять услуги независимо или во взаимодействии с другими подобными системами.

Каждое предприятие представляет собой такую ​​производственную систему, которая включает в себя набор взаимосвязанных и целенаправленных элементов, предназначенных для достижения определенных целей: материалы (здания, оборудование, сырье, оборудование, оборудование, конструкторская и технологическая документация и др.), персонал, информация (планы, норм, стандартов, документооборота и т. д.), финансовых, энергетических и других ресурсов, обеспечивающих выпуск соответствующих продуктов или продажу услуг. Существование такой системы обусловлено наличием спроса на товары или услуги, возникающие на рынке. Их основной и определяющей частью являются производственные процессы, для организации которых необходим инструмент, труд и рабочая сила.

Использование математики в экономике принимает форму экономико-математического моделирования. Используя экономико-математическую модель, изображен тот или иной реальный экономический процесс. Такая модель может быть построена только на основе глубокого теоретического изучения экономической сущности процесса, только в этом случае математическая модель будет адекватна реальному экономическому процессу, будет объективно ее отражать.

Математическое моделирование экономических явлений и процессов является важным инструментом экономического анализа. Это позволяет получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю структуру и внешние связи. Модель — это условное изображение объекта управления (исследования), оно создается субъектом управления (исследования) таким образом, чтобы отображать характеристики объекта — свойства, взаимосвязи, структурные и функциональные параметры и т. д., существенные с целью контроля (исследования). Содержание метода моделирования состоит из построения модели на основе предварительного исследования объекта и выделения его основных характеристик, экспериментального или теоретического анализа модели, сравнения результатов с данными об объекте и обновления модели.

В экономическом анализе в основном используются математические модели, которые описывают изучаемое явление или процесс с использованием уравнений, неравенств, функций и других математических средств. Существуют математические модели с количественными характеристиками, записанными в виде формул, численные модели с конкретными числовыми характеристиками, логические, записано с использованием логических выражений и графики. выражается в графических изображениях. Модели, реализованные с использованием электронных компьютеров, называются машинными или электронными.

Экономико-математическая модель должна быть адекватна реальности, отражать существенные аспекты и взаимосвязи исследуемого объекта. Отметим принципиальные особенности построения экономико-математической модели любого рода. Процесс моделирования можно разделить на три этапа:

1. анализ теоретических закономерностей, присущих изучаемому явлению или процессу, и эмпирических данных о его структуре и особенностях; на основе этого анализа формируются модели;
2. определение методов, с помощью которых можно решить проблему;
3. анализ результатов.

Во время экономико-математического моделирования часто возникает ситуация, когда изучаемая экономическая система имеет слишком сложную структуру, математические методы, схемы, которые охватывали бы все основные особенности и взаимосвязи этой системы, не были разработаны. Такой экономической системой, например, является экономика предприятия в целом, по динамике, развитию. Возникает необходимость упростить исследуемый объект, исключения из анализа некоторых его вторичных признаков. Чтобы привести эту упрощенную систему к классу уже известных структур, которые могут быть математически описаны и проанализированы. В то же время степень упрощения должна быть такой, чтобы в модель были включены все признаки, необходимые для данного экономического объекта в соответствии с целью исследования.

Важным моментом на первом этапе моделирования является четкое изложение конечной цели построения модели, а также определение критерия, по которому будут сравниваться различные решения. В экономическом анализе такими критериями могут быть: самая высокая прибыль, самые низкие производственные затраты, максимальная загрузка оборудования, производительность труда и т. д. В задачах математического программирования такой критерий отражается целевой функцией.

Например, необходимо проанализировать производственную программу по разработке продукта, чтобы определить резервы увеличения прибыли от последствий структурного сдвига в ассортименте. В этом случае критерием оптимальности при построении экономико-математической модели является максимальная прибыль.

При постановке задач математического программирования обычно предполагается, что ресурсы ограничены, которые должны быть выделены для производства продуктов. Поэтому очень важно определить, какие ресурсы являются решающими для исследуемого процесса и в то же время ограничивают их предложение. Если для производства продукции используются все виды производственных ресурсов, включая сырье, рабочую силу, мощности оборудования и т. д., то необходимо знать потребление каждого типа ресурса на единицу продукции.

Все ограничения, отражающие экономический процесс, должны быть последовательными, то есть должно быть по крайней мере одно решение проблемы, которое удовлетворяет всем ограничениям.

Построение или моделирование системы конечных факторов для анализируемого экономического показателя экономической деятельности может быть выполнено как формально, так и эвристически на основе качественного анализа сущности экономического явления, отраженного с помощью этого эффективного показателя. Моделирование факторной системы основано на следующих экономических критериях для выявления факторов как элементов факторной системы: причинность, достаточная специфичность, независимость существования, ответственность. С формальной точки зрения факторы, включенные в систему факторов, должны быть количественно измеримыми.

При детерминированном моделировании факторных систем можно выделить небольшое количество типов конечно-факторных систем, которые чаще всего встречаются при анализе экономической деятельности.

Стохастический анализ направлен на изучение косвенных связей, то есть косвенных факторов (если невозможно определить непрерывную цепочку прямой коммуникации). Это приводит к важному выводу о связи между детерминистическим и стохастическим анализом: поскольку прямые связи должны быть изучены в первую очередь, стохастический анализ носит вспомогательный характер. Стохастический анализ выступает в качестве инструмента для углубления детерминированного анализа факторов, для которых невозможно построить детерминистическую модель.

Стохастическое моделирование факторных систем взаимосвязей отдельных аспектов хозяйственной деятельности основано на обобщении законов изменения значений экономических показателей — количественных характеристик факторов и экономических результатов. Количественные параметры связи определяются путем сравнения значений исследуемых показателей в совокупности экономических объектов или периодов. Таким образом, первой предпосылкой для стохастического моделирования является способность составлять ряд наблюдений, то есть способность повторно измерять параметры одного и того же явления в различных условиях.

Следующие математические и статистические методы стохастического моделирования экономических явлений и процессов нашли применение в экономических исследованиях: оценка взаимосвязи и корреляции между показателями; оценка статистической значимости отношений; регрессионный анализ; выявление параметров периодических колебаний экономических показателей; группировка многомерных наблюдений, дисперсионный анализ; современный факторный (компонентный) анализ; трансформационный анализ.

Необходимость включения математических и статистических методов в методологию анализа хозяйственной деятельности предприятий зависит от значимости количественных (статистических) задач, решаемых с помощью этих методов. Можно выделить следующие наиболее типичные классы задач анализа хозяйственной деятельности, для решения которых применяются методы стохастического моделирования:

• изучение наличия, направленности и интенсивности взаимосвязей показателей экономической деятельности;
• ранжирование и классификация факторов экономических явлений;
• выявление аналитической формы связи между показателями;
• ранжирование и классификация субъектов хозяйствования;
• выявление наиболее информативных (обобщающих) показателей хозяйственной деятельности;
• анализ структурных изменений в совокупности объектов анализа;
• нахождение общих закономерностей функционирования объекта;
• построение усредненных нормативов экономической деятельности.

Для решения вышеуказанных задач используются математические и статистические методы стохастического моделирования, такие как группировка многомерных наблюдений, корреляционный и регрессионный анализ, таксономический метод, дисперсионный анализ, методы причинного анализа, компонентный анализ.

Основой стохастического моделирования является способность выстраивать взаимосвязи между функционированием объекта анализа на основе статистического обобщения законов изменения значений показателей экономической деятельности. Например, на основе анализа зависимости производительности капитала от показателей технического и организационного уровня для набора литейных объектов построена модель стохастической зависимости типа.

Основной задачей корреляционно-регрессионного анализа является определение формы и тесноты связи между эффективными и факторными показателями. Под формой коммуникации понимают тип аналитической формулы, выражающей зависимость эффективного показателя от изменения фактора. Существует прямая связь, когда при увеличении (уменьшении) значений факторного показателя наблюдается тенденция к увеличению (уменьшению) значений эффективного показателя. В противном случае между индикаторами есть обратная связь. (ему соответствует уравнение прямой), когда наблюдается тенденция к равномерному увеличению или уменьшению эффективного показателя, в противном случае форма общения называется изогнутой (ей соответствуют уравнения параболы, гиперболы и т. д.).

Основные модели корреляционного анализа: коэффициент парной корреляции, коэффициент частичной корреляции, коэффициент множественной корреляции, коэффициент детерминации.

Математические модели корреляционного анализа в виде коэффициентов имеют ограниченные аналитические возможности. Зная только направление ковариации показателей и плотность общения, невозможно определить закономерности формирования уровня эффективного показателя под воздействием изучаемых факторов, оценить интенсивность их влияния и классифицировать факторы в основной и дополнительный. Для этих целей используются модели регрессионного анализа. Линейная модель (уравнение) регрессионного анализа может быть представлена ​​как коэффициенты регрессии показывают интенсивность влияния факторов на эффективный показатель.

В системе управления важна объективная оценка достигнутого уровня экономической активности. Трудность получения такой оценки связана с тем, что экономическая деятельность и ее результаты охватывают множество различных процессов и не выражаются одним общим показателем. Следовательно, необходимо измерять и оценивать различные аспекты экономической деятельности, а затем объединять частные оценки в одну интегрированную.

Экономико-математическая модель для оптимизации производственной программы

Работа над пятилетними и годовыми планами экономического и социального развития на предприятиях (в холдингах) начинается с определения структуры продуктов, то есть номенклатуры и количества каждой единицы производимой продукции. Формирование производственной программы обычно связано с анализом различных вариантов структуры планируемого продукта, сопоставлением его со спросом, сложностью работы с производственными мощностями и наличием трудовых ресурсов, с возможностью материально-технической базы. Поддержка, особенно скоординированные поставки заготовок, полуфабрикатов и, наконец, достижение утвержденных показателей с точки зрения объема производства и продаж, прибыли и издержек, роста производительности труда и других показателей. Таким образом, в традиционном «ручном» методе составления производственного плана присутствуют элементы оптимизации. Но «ручной» метод оптимизации далек от научного, поскольку в нем отсутствуют критерий оптимальности (функция-цель) и экономико-математическая модель.

Критерий оптимальности должен отражать цель производства, заключающуюся в повышении уровня удовлетворения потребностей общества и получении достаточного финансового результата.

В свою очередь, уровень удовлетворения потребностей характеризуется как количеством производимой и необходимой потребителям продукции, так и высоким качеством поставляемой продукции. Этот критерий оптимальности (по сравнению с прибылью и прибыльностью) разрушает устоявшиеся взгляды на планирование производства, что иногда приводит к искажению эффективности производства и нежелательным сдвигам в структуре производственной программы.

Производственный план является основной проблемой в теории производства и распределения. Это вытекает из необходимости оптимального распределения предметов, средств труда и людей, приводящих их в действие, которые ограничены в определенный период.

Предприятия решают задачу оптимизации производственной программы по максимально локальному критерию на основе отношений с организациями, занимающимися распределением капитала, посредством которых определяются спрос и требования к продукции, а также обеспечивается удовлетворение потребностей общества. Весь спектр работ по оптимизации производственных планов должен определяться поэтапно в этой последовательности.

Изучение (проверка) объекта оптимизации, а именно: выявление особенностей производства — частоты выпускаемой продукции, ее серийности и общих технических и эксплуатационных свойств, установление спроса на продукцию предприятия, в том числе превышение спроса над достигнутые производственные возможности предприятия по выпуску продукции к началу планового периода, наличие разумных норм планирования выпускаемой продукции.

Идентификация номенклатуры и структуры плана, сериализация продуктов, изучение общности их назначения и технических и эксплуатационных свойств каждого продукта важны для построения экономической модели, для оценки и сравнения различных вариантов плана. с точки зрения операционной эффективности и применения всей массы планируемой продукции. Для тех предприятий, объем производства которых состоит из одного или двух ведущих продуктов, поиск предельного значения объема производства осуществляется путем сравнения различных вариантов плана с уровнем эффективного использования производственных мощностей или других ресурсов.

Особенностью многономенклатурного производства является то, что спрос может превышать достигнутый уровень производства и производственные мощности предприятия одновременно по нескольким или по абсолютному большинству товаров с различными потребительскими свойствами (качеством) и трудоемкостью. В таких условиях предприятие вынуждено принимать решение о предпочтении развития производства определенной продукции. В то же время важно, чтобы выбор структуры производственного плана оправдывался не только выгодой производителя, но и стремлением достичь максимальной эффективности и перспектив, в том числе эффективности использования продукции.

Построение экономико-математической модели оптимальной производственной программы должно зависеть от поставленной экономической задачи, выбора критерия оптимальности и ограничений.

Система планового управления экономикой предполагает взаимовыгодные отношения между производителем и потребителем, что является неотъемлемым преимуществом экономической системы в целом. Таким образом, при принятии решения о том, какие продукты в многономенклатурном производстве следует отдавать предпочтение, чтобы максимизировать эффект всех производимых продуктов (при неполном удовлетворении спроса), наряду с увеличением массы продуктов, необходимо учитывать Операционная эффективность каждого продукта в отдельности, а затем и всей продукции, выпускаемой предприятием, в разных вариантах производственного плана.

Если бы предприятия имели объективные оценки эффективности каждого продукта, то разработанная производственная программа была бы оценена как интегральный показатель эффективности продукта с учетом, прежде всего, сферы потребления (поскольку, как правило, основная доля эффекта получается при эксплуатации продукта) и сфере производства этих продуктов. В этом случае полезность увеличения производства определенных продуктов будет оцениваться как объективный показатель роста эффективности.

Однако задача определения эффективности использования продукции в народном хозяйстве достаточно сложна. Это связано с тем, что продукты большинства отраслей промышленности могут использоваться на самых разных объектах с точки зрения эксплуатации, создавая тем самым широкий спектр оценок эффективности их использования.

Чтобы получить качественные характеристики различных вариантов производственной программы, вам необходимо оценить эффективность применения (эксплуатации) каждого продукта и всех запланированных продуктов в целом. Известно, что номенклатура и структура продуктов должны энергично реагировать на меняющиеся потребности общества. Поэтому его следует оценивать не столько по объему (тыс. руб. в постоянных ценах), сколько по его эффективности для потребления. Для этого необходимо систематически изучать эффективность данного товара, спрос и спрос на него. Это имеет принципиальное значение для формирования производственных планов. На практике во многих случаях номенклатура и структура плана отражают преимущества производства (при формировании прибыли и других формирующих капитал показателей) и недостаточную эффективность его использования у потребителей.

Требования к продуктам, и даже более высокоэффективным, как правило, превосходят производственные возможности по их полному удовлетворению. Это, по нашему мнению, является причиной несоответствия между спросом и возможностями их полного удовлетворения. С этих позиций производственные мощности в каждом плановом периоде отражают фиксированные возможности производства для выполнения определенного объема работ, а в задаче оптимального программирования выступает основным ограничением.

В условиях многономенклатурного производства поиск оптимальной структуры продукта с точки зрения может рассматриваться с точки зрения эффективного распределения ресурсов и, прежде всего, производственных мощностей. Все условия, связанные с практическим решением этой экономической задачи, являются согласованными и разрешимыми экономико-математическим методом, поскольку существует цель, возможность количественного выражения критерия оптимальности и ограничения, максимизация целевой функции.

Выбор математического аппарата, с помощью которого оптимизируется многопродуктивная производственная программа предприятия, основан на том факте, что математическое программирование имеет набор оптимальных методов принятия решений в таких экономических и производственных ситуациях, когда необходимо найти крайнюю значение целевой функции нескольких переменных. Линейное программирование стало широко распространенным, поскольку в большинстве экономических задач основные зависимости выражаются линейными уравнениями или неравенствами, содержащими переменные (искомые оптимальные значения) только в первой степени. Эти задачи хорошо разработаны, имеют гармоничную теорию и решения.

В практику управления производственным объединением (холдингом) все чаще внедряются автоматизированные системы управления предприятием (АМС), информационные вычислительные центры (ИТЦ). Модели управления постоянно совершенствуются, сменяются поколения электронных компьютеров. На многих предприятиях и в холдингах успешно функционируют подсистемы автоматизированного оперативного контроля за движением производства, материально-технического обеспечения, контроля за выполнением бизнес-контрактов на поставку готовой продукции, учета выполнения внутренних показателей производственного учета, учета успешно функционируют решаются различные технические задачи по управлению станками и линиями с ЧПУ, рассчитываются показатели надежности новых продуктов и т. д.

Резервы эффективности автоматизированных систем управления заключаются в широком использовании задач планирования при планировании, которые по существу не задействованы. Основным содержанием научного метода оптимального планирования является возможность выбора наилучшего варианта из ряда альтернатив по выбранному критерию. Очевидно, что для выбора лучшего из множества вариантов вам необходимо иметь право варьировать производственные ресурсы по крайней мере в определенных пределах и быть независимым при принятии таких решений. По этой причине в работе настоятельно подчеркивается необходимость демократизации планирования, расширения прав объединений, предприятий при формировании производственной программы.

Оптимизация производственной программы

Современные условия бизнеса, характеризующиеся поворотом экономики страны к рыночным отношениям, требуют от предприятий оперативного реагирования на изменения спроса, подчиняя производство потребностям рынка. Необходимость реализации проблем, связанных с этим, требует решения комплекса задач, основной из которых является формирование рационального набора продуктов.

Разработка стратегических решений

При разработке этих решений применяются качественные методы, направленные на формирование экономического портфеля, который понимается как совокупность отдельных направлений деятельности и продуктов предприятия. Среди этих методов широко известны стратегические матрицы (матрица Бостонской консультативной группы, матрица «Дженерал-Элементаль-МакКинси», а также ряд других моделей).

Разработка оперативно-тактических решений

При разработке этих решений, как правило, применяются количественные методы, направленные на оптимизацию производственной программы предприятия в рамках тех направлений и видов деятельности, которые были выбраны на этапе разработки стратегических решений.

В данной работе рассматривается решение проблемы оптимизации производственной программы предприятия, которая заключается в поиске рационального сочетания цен и объемов продаж. Этот процесс занимает одно из центральных мест в системе управления производством, поскольку от него напрямую зависят конечные результаты деятельности предприятия.

Общепринятым критерием оптимальности при формировании производственной программы предприятия является максимальная прибыль от реализации продукции. Процесс определения оптимальных цен и объемов продаж отражается, прежде всего, в изменении веса отдельных видов продукции в общем объеме производства. Критерием изменения удельного веса отдельных видов продукции является показатель рентабельности продукции. В то же время считается, что увеличение общего объема продаж доли более высокодоходных продуктов обеспечивает наибольшую сумму прибыли.

Но всегда ли существует прямая зависимость между прибыльностью продукта и прибылью от его продажи? Другими словами, обеспечивает ли производственная программа, обеспечивающая максимальную прибыль, адекватную максимизацию эффективности производства, отраженную в показателе рентабельности продукции?

Для анализа согласованности вышеуказанных критериев необходимо построить функцию спроса и стоимости для каждого анализируемого вида продукта, которая, в свою очередь, определяет функцию прибыли и функцию доходности продукта.

Методы оптимизации

Процесс оптимизации является основой всей инженерной деятельности, поскольку функции специалиста состоят в том, чтобы, с одной стороны, разрабатывать новые, более эффективные и менее дорогие технические системы, а с другой — разрабатывать методы для повышения качества функционирование существующих систем.

На практике часто из множества возможных решений проблемы необходимо выбирать оптимальное. Например, из нескольких вариантов транспортировки сырья потребители должны выбрать самый дешевый, но тот, который учитывает ограничения на приемлемые условия доставки; из возможных планов резки материалов выберите тот, который позволит вам выполнить план с наименьшим количеством отходов и т. д.

Во многих случаях задача нахождения оптимального решения может быть формализована и решена точно или приближенно известными методами.

Оптимизация — это целенаправленная деятельность, которая заключается в получении наилучших результатов в соответствующих условиях.

Поиск оптимальных решений привел к созданию специальных математических методов, и уже в 18 веке были заложены математические основы оптимизации (вариационное исчисление, численные методы и т. д.). Однако до второй половины 20-го века методы оптимизации использовались очень редко во многих областях науки и техники, поскольку практическое использование методов математической оптимизации требовало огромных вычислительных усилий, что без компьютеров было чрезвычайно сложно, а в некоторых случаях невозможно , Особенно большие трудности возникли при решении задач оптимизации процессов в химической технологии из-за большого количества параметров и их сложной взаимосвязи. При наличии компьютеров задача значительно упрощается.

Постановка задачи оптимизации предполагает наличие конкурирующих свойств процесса, например: — количество продуктов — «расход сырья» — количество продуктов — «качество продукта». Выбор компромиссного варианта для этих свойств является процедурой. для решения задачи оптимизации.

При постановке задачи оптимизации необходимо:

1. Наличие объекта оптимизации и цели оптимизации. Кроме того, формулировка каждой задачи оптимизации должна требовать предельного значения только одной величины, то есть в то же время два или более критерия оптимизации не должны приписываться системе, поскольку почти всегда экстремум одного критерия не соответствует экстремум другого.
2. Наличие ресурсов оптимизации, что означает возможность выбора значений некоторых параметров оптимизируемого объекта. Объект должен иметь определенные степени свободы — контрольные действия.
3. Способность количественно оценить оптимизированное значение, поскольку только в этом случае мы можем сравнивать эффекты выбора определенных управляющих воздействий.
4. Учет ограничений.

Методы безусловной оптимизации подразделяются на методы одномерной и многомерной оптимизации.

Несмотря на то, что безусловная оптимизация функции одной переменной является простейшим типом задач оптимизации, она занимает центральное место в теории оптимизации как с теоретической, так и с практической точек зрения. Это связано с тем, что проблемы однопараметрической оптимизации достаточно распространены в инженерной практике и, кроме того, находят свое применение при реализации более сложных процедур многопараметрической оптимизации.

Общим для методов нелинейного программирования является то, что они используются при решении задач с нелинейными критериями оптимальности. Все методы нелинейного программирования являются методами числового поиска. Их суть заключается в определении набора независимых переменных, которые дают наибольший прирост оптимизируемой функции. Эта группа методов используется как для детерминированных, так и для случайных процессов.

Заключение

При детерминированном факторном анализе модель изучаемого явления не изменяется по экономическим объектам и периодам (поскольку соотношения соответствующих основных категорий стабильны). Если необходимо сравнить результаты деятельности отдельных хозяйств или одного хозяйства в определенные периоды, может возникнуть только вопрос сопоставимости количественных аналитических результатов, определенных на основе модели.

В стохастическом анализе, где сама модель составляется на основе комбинации эмпирических данных, предпосылкой для получения реальной модели является совпадение количественных характеристик отношений в контексте всех первоначальных наблюдений. Это означает, что изменение значений показателей должно происходить в рамках однозначной определенности качественной стороны явлений, характеристиками которых являются моделируемые экономические показатели (в пределах изменения не должно быть качественного скачка в характер отраженного явления). Следовательно, второй предпосылкой применимости стохастического подхода к моделированию отношений является качественная однородность населения (относительно изученных отношений).

Изученная закономерность изменения экономических показателей (моделируемых отношений) предстает в скрытой форме. Он переплетен со случайными (с точки зрения исследования) компонентами вариации и ковариации показателей. Закон больших чисел гласит, что только в большой совокупности регулярная связь оказывается более устойчивой, чем случайное совпадение направления изменения (случайная ковариация).

Это приводит к третьей предпосылке стохастического анализа — достаточному измерению (числу) набора наблюдений, которое позволяет идентифицировать изученные закономерности (моделируемые отношения) с достаточной достоверностью и точностью. Уровень надежности и точности модели определяется практическими целями использования модели в управлении бизнесом.

Четвертой предпосылкой стохастического подхода является наличие методов определения количественных параметров взаимосвязи экономических показателей из массовых данных о варьировании уровня показателей. Математический аппарат используемых методов иногда предъявляет особые требования к моделируемому эмпирическому материалу. Выполнение этих требований является важной предпосылкой для применимости методов и достоверности результатов.

Главная особенность стохастического факторного анализа состоит в том, что невозможно составить модель с помощью качественного (теоретического) анализа, необходим количественный анализ эмпирических данных.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник