Способ определения точек пересечения прямой с плоскостью

Точка пересечения прямой и плоскости онлайн

С помощю этого онлайн калькулятора можно найти точку пересечения прямой и плоскости. Дается подробное решение с пояснениями. Для нахождения координат точки пересечения прямой и плоскости задайте вид уравнения прямой («канонический» или «параметрический» ), введите данные в уравнения прямой и плоскости и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Точка пересечения прямой и плоскости − теория, примеры и решения

1. Точка пересечения плоскости и прямой, заданной в каноническом виде

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы прямая L₁:

,

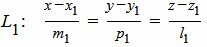(1)

α: Ax+By+Cz+D=0.

(2)

Найти точку пересечения прямой L₁ и плоскости α (Рис.1).

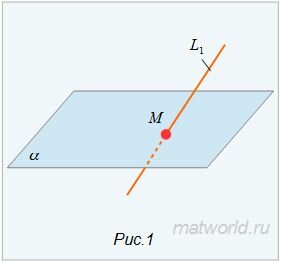Запишем уравнение (1) в виде системы двух линейных уравнений:

,

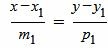(3)

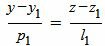(4)

Сделаем перекрестное умножение в уравнениях (3) и (4):

Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

Решим систему линейных уравнений (2), (5), (6) с тремя неизвестными x, y, z. Для этого в уравнении (2) переведем свободный член в правую часть уравнения и запишем эту систему в матричном виде:

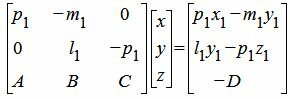(7)

Как решить систему линейных уравнений (11)(или (2), (5), (6)) посмотрите на странице Метод Гаусса онлайн или на примерах ниже. Если система линейных уравнениий (7) несовместна, то прямая L₁ и плоскость α не пересекаются. Если система (7) имеет множество решений, то прямая L₁ лежит на плоскости α. Единственное решение системы линейных уравнений (7) указывает на то, что это решение определяет координаты точки пересечения прямой L₁ и плоскости α.

Замечание. Если прямая задана параметрическим уравнением, то уранение прямой нужно приводить к каноническому виду и применить метод, описанный выше, или же

2. Точка пересечения плоскости и прямой, заданной в параметрическом виде.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат задана прямая L₁ в параметрическом виде:

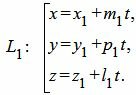(8)

α: Ax+By+Cz+D=0.

(9)

Задачу нахождения нахождения точки пересечения прямых L₁ и плоскости α можно решить разными методами.

Метод 1. Приведем уравнения прямой L₁ к каноническому виду.

Для приведения уравнения (8) к каноническому виду, выразим параметр t через остальные переменные:

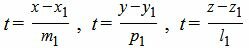(10)

Так как левые части уравнений (10) равны, то можем записать:

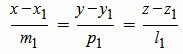(11)

Далее, для нахождения точки пересечения прямой и плоскости нужно воспользоваться параграфом 1.

Метод 2. Для нахождения точки пересечения прямой L₁ и плоскости α решим совместно уравнения (8) и (9). Из уравнений (8) подставим x, y, z в (9):

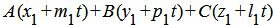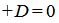(13)

Откроем скобки и найдем t:

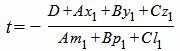(14)

Если числитель и знаменатель в уравнении (14) одновременно равны нулю, то это значит, что прямая L₁ лежит на полскости α. Если в уравнении (14) числитель отличен от нуля, а знаменатель равен нулю, то прямая и плоскость параллельны.

Если же числитель и знаменатель в уравнении (14) отличны от нуля, то прямая и плоскость пересекаются в одной точке. Для нахождения координат точки пересечения прямой L₁ и плоскости α подставим полученное значение t из (14) в (8).

3. Примеры нахождения точки пересечения прямой и плоскости.

Пример 1. Найти точку пересечения прямой L₁:

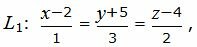(15)

Представим уравнение (15) в виде двух уравнений:

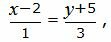(17)

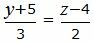(18)

Сделаем перекрестное умножение в уравнениях (17) и (18):

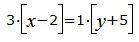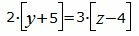Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

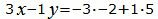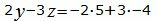Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (19) и (20). Для этого переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (19) и (20):

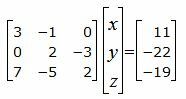(21)

Решим систему линейных уравнений (21) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

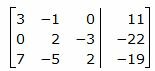Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строку 3 со строкой 1, умноженной на −7/3:

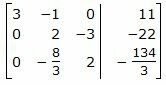Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на 4/3:

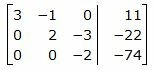Второй этап. Обратный ход Гаусса.

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строку 2 со строкой 3, умноженной на −3/2:

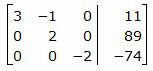Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на 1/2:

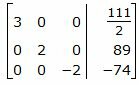Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

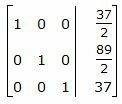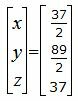Ответ. Точка пересечения прямой L₁ и плоскости α имеет следующие координаты:

Пример 2. Найти точку пересечения прямой L₁:

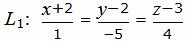(22)

Представим уравнение (22) в виде двух уравнений:

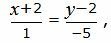(24)

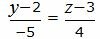(25)

Сделаем перекрестное умножение в уравнениях (24) и (25):

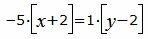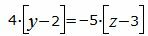Откроем скобки и переведем переменные в левую часть уравнений а остальные элементы в правую часть:

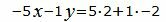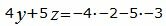Для нахождения точки пересечения прямой L₁ и плосклсти α нужно решить совместно уравнения (2), (26) и (27). Переведем в уравнении (2) свободный член на правую сторону уравнения и построим матричное уравнение для системы линейных уравнений (2), (26) и (27):

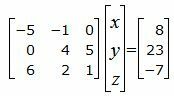(28)

Решим систему линейных уравнений (21) отностительно x, y, z. Для этого построим расширенную матрицу:

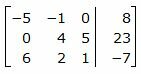Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 3 со строкой 1, умноженной на 6/5:

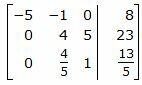Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на −1/5:

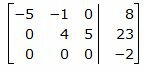Из расширенной матрицы восстановим систему линейных уравнений:

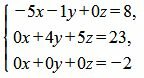(29)

Легко можно заметить, что последнее уравнение в (29) несовместна, так как несуществуют такие x, y, z чтобы выполнялось это равенство. Следовательно система линейных уравнений (2), (26) и (27) несовместна. Тогда прямая L₁ и плоскость α не пересекаются, т.е. они параллельны.

Ответ. Прямая L₁ и плоскость α параллельны, т.е. не имеют общую точку.

Пример 3. Найти точку пересечения прямой в параметрическом виде L₁:

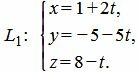(30)

Решение. Для нахождения точки пересечения прямой L₁ и плоскости α нужно найти такое значение t, при котором точка M(x, y, z) удовлетворяет уравнению (31). Поэтому подставим значения x, y, z из (30) в (31):

Упростив уравнение, получим:

Как видим, любое значение t удовлетворяет уравнению (33), т.е. любая точка на прямой L₁ удовлетворяет уравнению плоскости α. Следовательно прямая L₁ лежит на плоскости α.

Ответ. Прямая L₁ лежит на плоскости α.

Источник

Определение точки пересечения прямой с плоскостью

Для определения точки пересечения прямой с плоскостью пользуемся следующим алгоритмом: прямую заключаем во вспомогательную плоскость, находим линию пересечения этих двух плоскостей (заданной и вспомогательной), и линия пересечения плоскостей в пересечении с заданной прямой даст искомую точку. Последним этапом в построении является определение видимости прямой при помощи конкурирующих точек.

Пример1. Плоскость задана следами (рис.70)

Рис.70

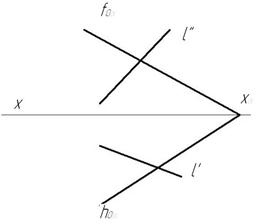
1. Для построения точки пересечения прямой lс плоскостью необходимо через прямую провести вспомогательную плоскость частного положения, например, фронтально-проецирующую β 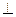π₂, l» f_оβ, f_оβ – собирающий след, h_оβ х (рис.71).

Рис.71

2. Строим линию пересечения MN заданной и вспомогательной плоскости М’=h_оα∩ h_оβ, N»= f_оβ∩ f_оα (рис.72).

Рис.72

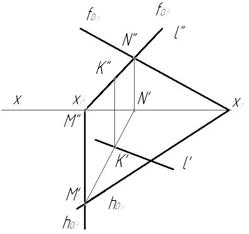
3. Определяем точку пересечения К заданной прямой l с линией пересечения MN. К’=М’N’∩l ‘, К» – в пересечении линии проекционной связи, проведенной из К’ и l ».

4. Видимость прямой l в случае задания плоскости следами не определяем.

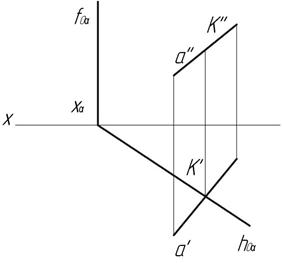
Пример 2. Пересечение прямой с проецирующей плоскостью (рис.73).

При построении точки пересечения прямой с проецирующей плоскостью задача упрощается, т.к. одна из проекций искомой точки будет лежать на собирающем следе. На рис.73 дана горизонтально-проецирующая плоскость. Искомая точка К будет одновременно принадлежать плоскости α и прямой а.

Рис.73

Пример 3. Плоскость задана плоской фигурой (рис.74).

Рис.74

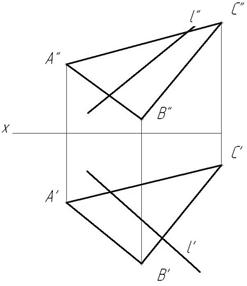
Через прямую l проводим вспомогательную плоскость частного положения, например, горизонтально-проецирующую β π₁.l‘ h_оβ, h_оβ – собирающий след, f_оβ х (рис.75).

Рис.75

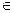
2. Строим линию пересечения MN заданной и вспомогательной плоскостей. М’=А’С’∩ hоβ М» А»С» и N’=В’С’∩ hоβ N» »ѻ (рис. 76).

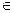
3. Строим точку пересечения К заданной прямой l с линией пересечения МN. К»= М»N»∩l». К’ находится в пересечении линии проекционной связи, проведенной из К» и М’N’.

4. Определяем видимость прямой относительно ΔАВС с помощью конкурирующих точек.

Определяем видимость относительно плоскости π₂ .Отметим фронтальную проекцию 1» совпадающую с 2». Горизонтальную проекцию 2′ отметим на А’С’, а 1′ на l’. Горизонтальная проекция 1′ лежит перед 2′, следовательно, фронтальная проекция 2» не видима относительно π₂. Точка 1 лежит на прямой l, она видима на π₂, следовательно, фронтальная проекция l» от 1″2» до К» видима, в точке К» видимость меняется на противоположную.

Определим видимость прямой l относительно плоскости π₁. Отметим горизонтальную проекцию 3′, совпадающую с горизонтальной проекцией М’. М» 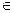А»С» уже отмечена, 3» l’‘. Фронтальная проекция М» лежит выше фронтальной проекции 3», следовательно, точка М видима относительно π₁. Точка 3 лежит на l, следовательно, от М’≡3′ до К’, горизонтальная проекция l’ невидима. В горизонтальной проекции К’ видимость меняется на противоположную. За границами ΔАВС прямая l везде видима.

Рис.76

Источник