Способ определения силы архимеда

Архимедова сила

О чем эта статья:

Сила: что это за величина

Прежде чем говорить о силе Архимеда, нужно понять, что это вообще такое — сила.

В повседневной жизни мы часто видим, как физические тела деформируются (меняют форму или размер), ускоряются и тормозят, падают. В общем, чего только с ними не происходит! Причина любых действий или взаимодействий тел — ее величество сила.

Сила — это физическая векторная величина, которая воздействует на данное тело со стороны других тел. Сила измеряется в ньютонах — единице измерения, которую назвали в честь Исаака Ньютона.

Поскольку сила — величина векторная, у нее, помимо модуля, есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В этом случае результат выражается в направлении движения.

Открытие закона Архимеда

Так вышло, что закон Архимеда известен не столько своей формулировкой, сколько историей возникновения.

Легенда гласит, что царь Герон II попросил Архимеда определить, из чистого ли золота сделана его корона, при этом не причиняя вреда самой короне. То есть расплавить корону или растворить — нельзя.

Взвесить корону Архимеду труда не составило, но этого было мало — нужно ведь определить объем короны, чтобы рассчитать плотность металла, из которого она отлита.

Рассчитать плотность металла, чтобы установить, золотая ли корона, можно по формуле плотности.

Формула плотности тела

ρ = m/V

ρ — плотность тела [кг/м 3 ]

m — масса тела [кг]

V — объем тела [м 3 ]

Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. Тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему.

Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый закричал «Эврика!» и побежал докладывать о своей победе в царский дворец (и так торопился, что даже не оделся). 🤦🏻‍♂️

Формула и определение силы Архимеда для жидкости

На поверхность твердого тела, погруженного в жидкость, действуют силы давления. Эти силы увеличиваются с глубиной погружения, и на нижнюю часть тела будет действовать со стороны жидкости большая сила, чем на верхнюю.

Равнодействующая всех сил давления, действующих на поверхность тела со стороны жидкости, называется выталкивающей силой или силой Архимеда. Истинная причина появления выталкивающей силы — наличие различного гидростатического давления в разных точках жидкости.

Определение архимедовой силы для жидкостей звучит так:

Выталкивающая сила, действующая на тело, погруженное в жидкость, равна по модулю весу вытесненной жидкости и противоположно ему направлена.

Формула архимедовой силы для жидкости

ρ_ж — плотность жидкости[кг/м 3 ]

V_погр — объем погруженной части тела [м 3 ]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2 .

А теперь давайте порешаем задачки, чтобы закрепить, как вычислить архимедову силу.

Задача 1

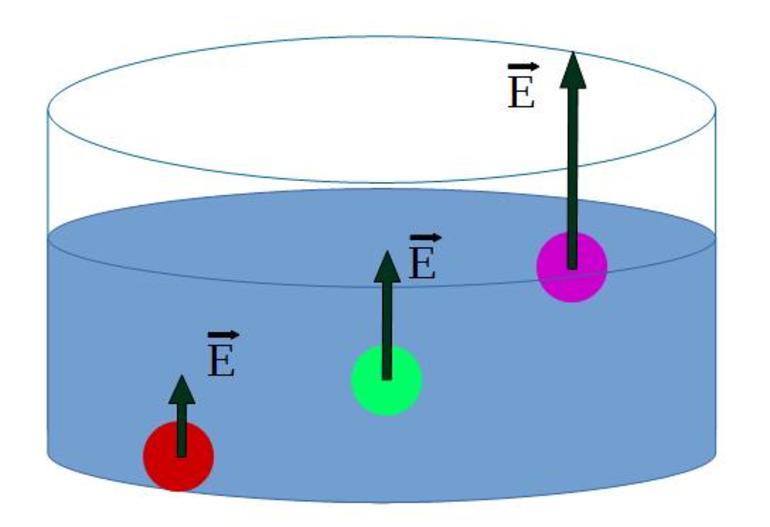
В сосуд погружены три железных шарика равных объемов. Одинаковы ли силы, выталкивающие шарики? Плотность жидкости вследствие ничтожно малой сжимаемости на любой глубине считать примерно одинаковой.

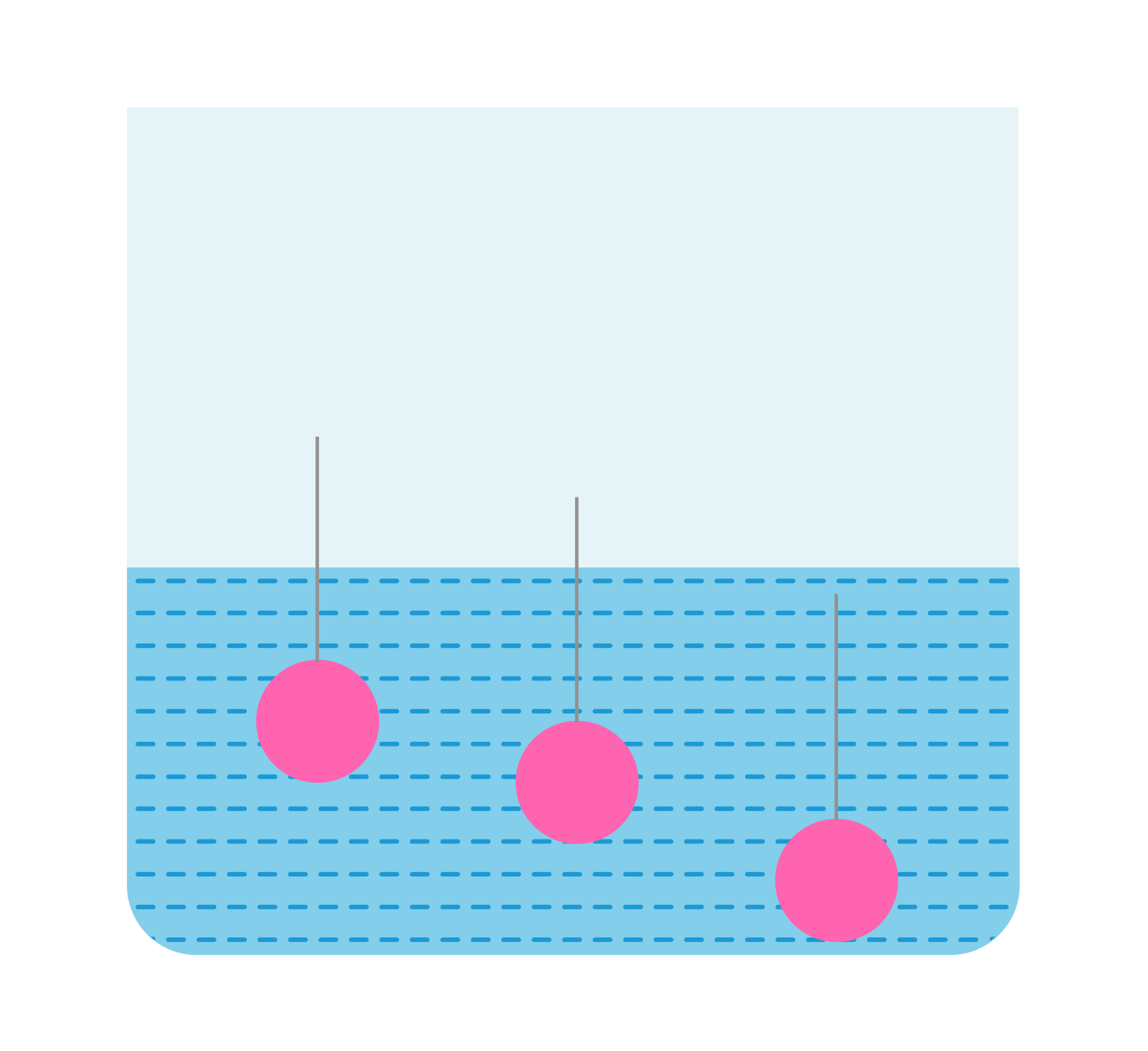
Решение

Да, так как объемы одинаковы, а архимедова сила зависит от объема погруженной части тела, а не от глубины.

Задача 2

На графике показана зависимость модуля силы Архимеда F_Арх, действующей на медленно погружаемый в жидкость кубик, от глубины погружения x. Длина ребра кубика равна 10 см, его нижнее основание все время параллельно поверхности жидкости. Определите плотность жидкости. Ускорение свободного падения принять равным 10 м/с 2 .

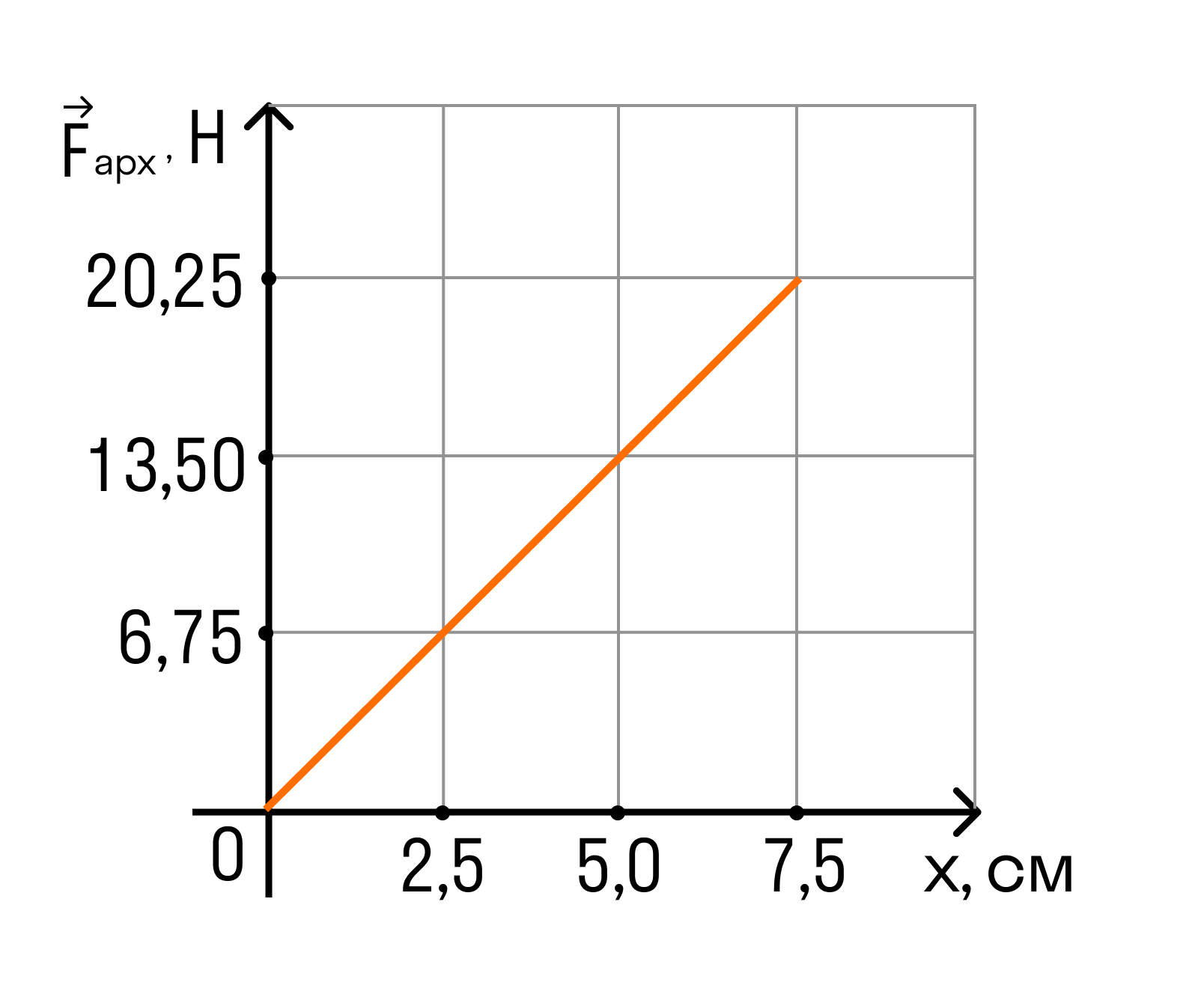
Решение

Сила Архимеда, действующая на кубик, равна F_Арх = ρ_жgV_погр.

V_погр. — объем погруженной части кубика,

ρ_ж — плотность жидкости.

Учитывая, что нижнее основание кубика все время параллельно поверхности жидкости, можем записать:

где а — длина стороны кубика.

ρ = F_Арх / ga 2 x

Рассматривая любую точку данного графика, получим:

ρ = F_Архga 2 x = 20,25 / 10 × 7,5 × 10 -2 = 2700 кг/м 3

Ответ: плотность жидкости равна 2700 кг/м 3 .

Условия плавания тел

Из закона Архимеда вытекают следствия об условиях плавания тел.

Погружение

Плавание внутри жидкости

Плавание на поверхности жидкости

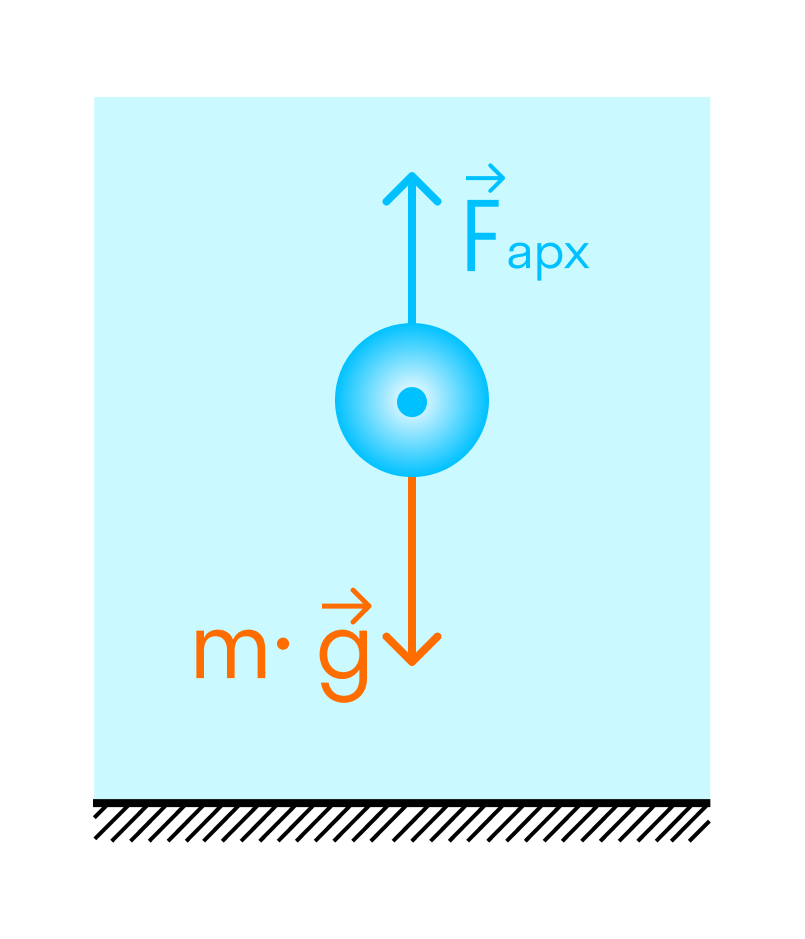
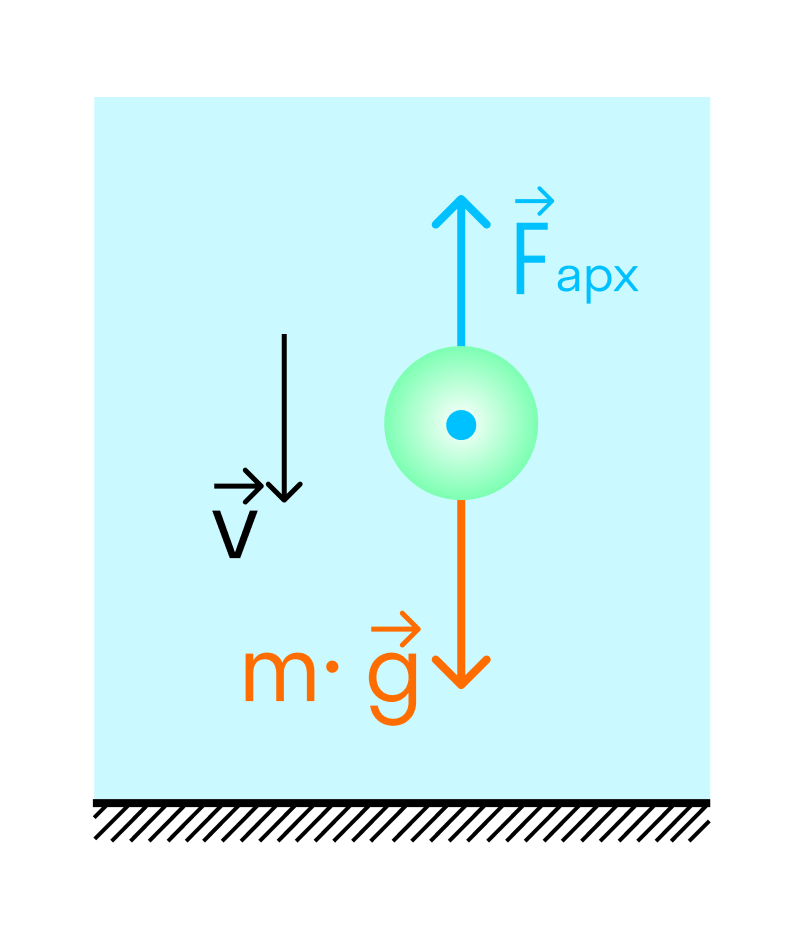
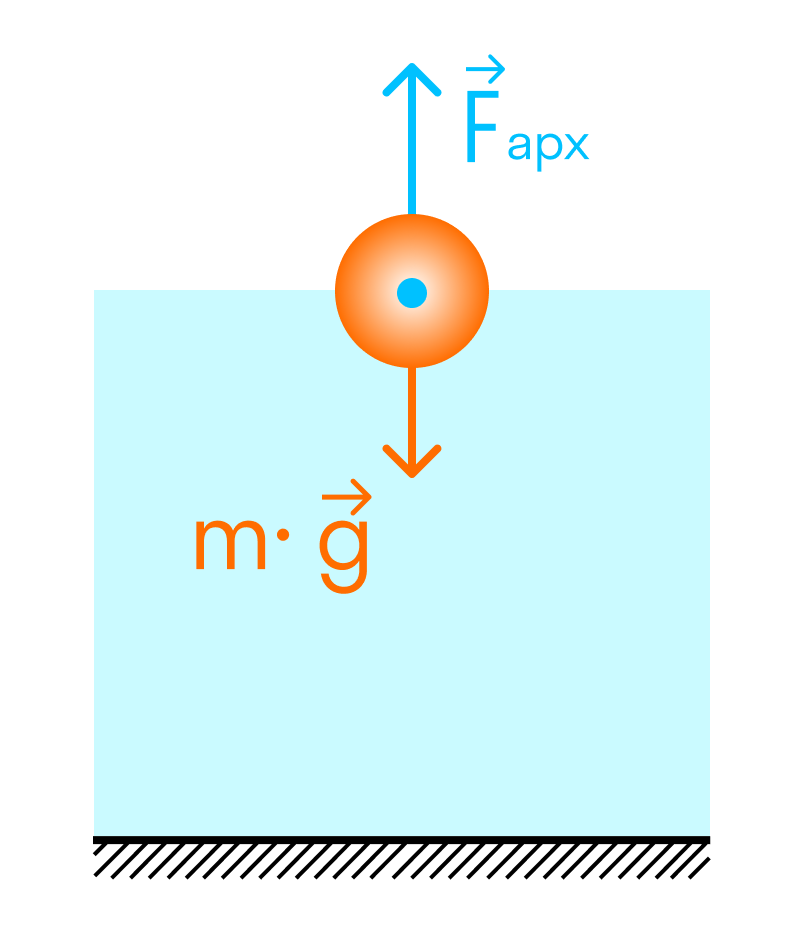
Если плотность тела меньше плотности жидкости или газа — оно будет плавать на поверхности.

Почему корабли не тонут?

Корабль сделан из металла, плотность которого больше плотности воды. И, по идее, он должен тонуть. Но дело в том, что корпус корабля заполнен воздухом, поэтому общая плотность судна оказывается меньше плотности воды, и сила Архимеда выталкивает его на поверхность. Если корабль получит пробоину, то пространство внутри заполнится водой — следовательно, общая плотность корабля увеличится. Судно утонет.

В подводных лодках есть специальные резервуары, которые заполняют водой или сжатым воздухом. Если нужно уйти на глубину — водой, если подняться — сжатым воздухом. Рыбы используют такой же принцип в плавательном пузыре — наполняют его воздухом, чтобы подняться наверх.

Человеку, чтобы не утонуть, тоже достаточно набрать в легкие воздух и не двигаться — вода будет выталкивать тело на поверхность. Именно поэтому важно не тратить силы и кислород в легких на панику и борьбу, а расслабиться и позволить физическим законам сделать все за нас.

Формула и определение силы Архимеда для газов

На самом деле тут все очень похоже на жидкости. Начнем с формулировки закона Архимеда:

Выталкивающая сила, действующая на тело, погруженное в газ, равна по модулю весу вытесненного газа и противоположно ему направлена.

Формула архимедовой силы для газов

ρ_г — плотность газа [кг/м 3 ]

V_погр — объем погруженной части тела [м 3 ]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2 .

Сила Архимеда для газов действует аналогично архимедовой силе для жидкостей. Давайте убедимся в этом, решив задачку.

Задача

Груз какой максимальной массы может удерживать воздушный шар с гелием объема 0,3 м 3 , находясь в атмосфере Земли? Плотность воздуха равна 1,3 кг/м 3 . Гелий считать невесомым.

Решение

Подставляем значения и получаем:

По второму закону Ньютона для инерциальных систем отсчета:

Выражаем массу груза и подставляем значения:

m = F_Арх / g = 0,39 / 10 = 0, 039 кг = 39 кг

Ответ: груз максимальной массы 39 г может удержать данный шарик с гелием.

Когда сила Архимеда не работает

Архимедова сила не работает лишь в трех случаях:

Невесомость. Главное условие возникновения Архимедовой силы — это наличие веса у среды. Если мы находимся в невесомости, холодный воздух не опускается, а горячий, наоборот, не поднимается.

Тело плотно прилегает к поверхности. Отсутствие газа или жидкости между поверхностью и телом свидетельствует об отсутствии выталкивающей силы — телу просто неоткуда выталкиваться.

Растворы и смеси. Если взять спирт, плотность которого меньше плотности воды, и смешать его с водой, получится раствор. На него не будет действовать сила Архимеда, несмотря на то, что плотность спирта меньше плотности воды — он просто растворится.

Источник

Сила Архимеда — природа, определение и формулы

Определение и формула

Закон Архимеда гласит, что если твёрдое тело погружено в жидкость, то на него действует выталкивающая сила, равная весу жидкости в объёме тела.

При некоторых обстоятельствах объём вещества одинаков объёму воды. В частности, когда твёрдый объект любого класса полностью погружен в воду, объём вытесненной воды должен быть равен объёму объекта. Кроме того, по определению силы Архимеда, при погружении объект получит плавучую силу, одинаковую весу вытесненной воды. Таким образом, объект, взвешенный в воздухе и затем взвешенный при погружении в воду, будет иметь эффективный вес, уменьшенный на вес вытесненной воды, если подъёмная сила воздуха незначительна.

Что произойдёт, если стакан наполнить водой доверху, а затем добавить кубики льда? Точно так же, как вода расплескалась через край, когда Архимед сел в свою ванну, жидкость в стакане выльется, если бросить туда кубики льда. Если взвесить разлившуюся воду (вес — это сила, направленная вниз), она будет равняться восходящей силе на предмете. По этой силе можно определить объём или среднюю плотность объекта.

При взвешивании в воздухе предмет получает силу выталкивания, равную весу воздуха, перемещаемого объектом. Однако плотность воздуха довольно мала (по сравнению с плотностью большинства твёрдых частиц), чтобы можно было пренебречь этой плавучей силой при взвешивании большинства твёрдых частиц в воздухе.

Формула силы Архимеда записывается как F = pgV, где:

1. F = выталкивающая сила тела (сила Архимеда). Единица измерения — ньютон.
2. p = давление объекта. Измеряется в Паскалях.
3. g = ускорение под действием силы тяжести. Метр на секунду в квадрате.
4. V = объём вытесненной жидкости в кубических метрах.

Формула принципа Архимеда полезна для нахождения силы, объёма смещённого тела или плотности жидкости, при условии, что некоторые из этих чисел известны.

При демонстрации закона Архимеда следует отметить, что в этом явлении многое зависит от гравитации. То есть сила плавучести, которая всегда противостоит элементу притяжения, на самом деле вызвана самой гравитацией. Давление внутри флюидов вырастает с увеличением глубины, поскольку внутри жидкости действует гравитационный вес сверху. Это давление, которое постоянно повышается, прикладывает силу к объекту, погруженному в воду, и увеличивается с глубиной жидкости. Результатом этого является плавучесть.

Принцип плавучести

Принцип Архимеда показывает подъёмную силу и вытеснение жидкости. Однако эта концепция может быть применена при рассмотрении вопроса плавания предметов. Пятый трактат Архимеда «О плавающих телах» гласит, что любой плавающий объект вытесняет собственный вес жидкости.

Другими словами, для предмета, плавающего на поверхности жидкости (например, лодки) или плавающего под водой (субмарина или дирижабль в воздухе), вес вытесненной жидкости равен весу объекта. Таким образом, только в особом случае плавания сила выталкивания, действующая на объект, равна его весу.

Например, существует блок из твёрдого железа, который весит 1 тонну. Поскольку железо почти в восемь раз плотнее воды, при погружении оно вытесняет только 1/8 тонны воды, что недостаточно для удержания его на плаву. Теперь следует предположить, что тот же железный блок преобразован в чашу. Он по-прежнему весит 1 тонну, но при помещении в жидкость он вытесняет больший объём воды, чем когда он был блоком. Чем глубже погружена железная чаша, тем больше воды она вытесняет и тем сильнее действует на неё выталкивающая сила. Когда плавучая сила равна 1 тонне, она не опустится дальше.

Когда лодка вытесняет вес воды, равный её собственному весу, она плавает. Каждый корабль, подводная лодка и дирижабль должны быть спроектированы так, чтобы смещать вес жидкости, по крайней мере, равный его собственному весу. Корпус 10000-тонного корабля должен быть достаточно широким, длинным и глубоким, чтобы вытеснять соответствующее количество тонн воды. Он нуждается в дополнительной грани для равновесия и борьбы с волнами, которые иначе заполнили бы его и, увеличив его массу, потопили корабль.

Практически принцип Архимеда позволяет рассчитывать плавучесть объекта, частично или полностью погруженного в жидкость:

1. Нисходящая сила на объекте — это просто его вес.
2. Восходящая или выталкивающая сила — это то, что указано выше по закону Архимеда.
3. Чистая сила — это разница между величинами силы выталкивания и её весом.

Следует отметить, что если вес объекта меньше, чем вес вытесняемой жидкости, объект будет испытывать подъём, как и происходит в случае с деревянным брусом, который остаётся ниже поверхности воды. Объект, который по своей природе тяжелее количества жидкости, которую он может вытеснить, утонет при освобождении, но в то же время испытает потерю веса, равную весу вытесненной жидкости. Фактически, когда дело доходит до взвешивания, необходимо внести поправку, чтобы иметь возможность компенсировать эффект плавучести окружающего его воздуха.

Хотя они связаны с этим, принцип плавания и концепция, согласно которой затопленный объект вытесняет объём жидкости, равный его собственному объёму, не являются законом Архимеда. Как указано выше, он приравнивает подъёмную силу к весу вытесненной жидкости.

Практическое применение

Принцип Архимеда имеет множество применений в области медицины и стоматологии и используется для определения плотности костей и зубов. В статье 1997 года, опубликованной в журнале Medical Engineering & Physics, исследователи использовали силу Архимеда для измерения объёма внутренней губчатой ​​части кости, которая может применяться в различных исследованиях старения, остеопороза, прочности костей, жёсткости и эластичности.

В статье, опубликованной в 2017 году в журнале Oral Surgery, использовались различные методы для определения воспроизводимости, одним из которых был принцип Архимеда. Его сравнивали с использованием конусно-лучевой компьютерной томографии для измерения объёма зубов. Тесты, сравнивающие закон и замера КЛКТ, показали, что последние будут точным инструментом при планировании стоматологических процедур.

Простой, надёжный и экономически эффективный проект для подводной лодки, описанный в статье 2014 года в журнале Informatics, Electronics and Vision, основан на принципе Архимеда. Конструкция этой прототипной субмарины использует расчёты, включающие массу, плотность и объём как подводной лодки, так и вытесненной воды, чтобы определить необходимый размер балластного танка. Он должен обозначить количество воды, способное его заполнить, и, следовательно, выяснить нижнюю границу глубины, на которую может погружаться подводная лодка.

Также можно наблюдать действие силы Архимеда в природе:

1. Определённая группа рыб использует принцип Архимеда, чтобы подниматься и спускаться по воде. Чтобы подняться на поверхность, они наполняют свой плавательный пузырь (воздушные мешки) газами.
2. В исследовании 2016 года использовался метод измерения теней, оставляемых водомерками, для понимания создаваемой ими кривизны поверхности воды. Авторы утверждают, что есть большой интерес к пониманию физики, стоящей за водными жуками, потому что это позволить создать экспериментальных биомиметических роботов, способных ходить по воде.
3. Плотность льда ледников и айсбергов меньше плотности океана, поэтому их частично выносит наверх.

Греческий учёный внёс огромный вклад в кораблестроение, сформировав критерии устойчивости плавающих объектов. Закон Архимеда также используется в широком спектре научных исследований, включая медицину, инженерию, энтомологию, инженерию и геологию.

Открытие закона

По легенде, некоторым своим современникам Архимед запомнился как человек, который бегал голым по улицам Сиракуз с криками «Эврика!», что в переводе означает «Нашёл!». Причиной возникновения этого события являлось данное Архимеду поручение доказать, что новая корона, сделанная для царя, не была из сплошного золота, как утверждал ювелир. Архимед долго работал над этой задачей, но никак не мог найти способ доказать недобросовестность изготовителя. Тем не менее проницательность грека привела к решению проблемы, поставленной перед ним Гиероном II.

Однажды Архимед наполнил ванну и заметил, что вода пролилась через край, когда он сел в неё. Тогда учёный понял, что жидкость, вытесненная его телом, была равна его весу. Оборудование для взвешивания объектов с достаточной точностью уже существовало, и теперь, когда Архимед также мог измерить объём, их соотношение дало бы плотность объекта — важный показатель чистоты, поскольку золото почти в два раза плотнее серебра и имеет значительно больший вес для того же объёма вещества при стандартных температурах и давлении.

Итак, зная, что золото тяжелее других металлов, которые мог бы использовать изготовитель короны, Архимед определил, что украшение не отличалось чистотой материала. Забыв о своей наготе, он побежал по улицам от дома к царю, крича: «Эврика!»

Источник