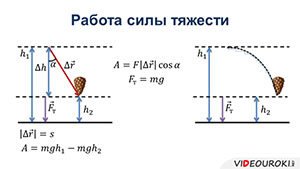
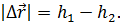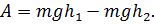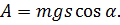Работа силы тяжести.
Рассмотрим тело, скользящее по наклонной плоскости с углом наклона α и высотой Н. Выразим Δх через H и α:
.
Учитывая, что сила тяжести Fт = mg составляет угол (90° — α) с направлением перемещения, используя формулу , получим выражение для работы силы тяжести Ag:
.
Из этой формулы видно, что работа силы тяжести зависит от высоты и не зависит от угла наклона плоскости.
Отсюда следует, что:
1. работа силы тяжести не зависит от формы траектории, по которой движется тело, а лишь от начального и конечного положения тела;
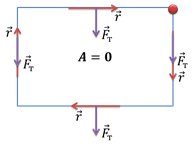
2. при перемещении тела по замкнутой траектории работа силы тяжести равна нулю, т. е. сила тяжести — консервативная сила (консервативными называются силы, обладающие таким свойством).
Работа сил реакции, как следует из рисунка, равна нулю, поскольку сила реакции (N) направлена перпендикулярно перемещению Δх.
Источник
Работа силы тяжести
Урок 30. Физика 10 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Работа силы тяжести»
Совсем недавно, мы изучили работу силы. Напомним, что работа силы равна произведению модуля силы, модуля перемещения и косинуса угла между направлениями силы и перемещения:
Рассмотрим теперь частный случай — работу силы тяжести при перемещении тела с высоты h1 на высоту h2.
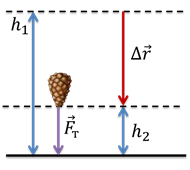
Первый случай — это падение тела вертикально вниз.
В этом случае, перемещение, конечно же, будет равно
Сила тяжести, как мы знаем, равна
.
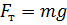
Поскольку сила тяжести направлена вертикально вниз, как и перемещение, косинус угла между направлениями этих векторов равен единице. Таким образом, мы получим, что работа силы тяжести равна:
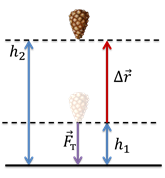
Второй случай — это когда тело, наоборот, подбрасывают вертикально вверх с высоты h1 на высоту h2.
В этом случае, угол между направлением силы тяжести и направлением перемещения составит 180 о . Это приводит нас к тому, что работа силы тяжести опять-таки равна:
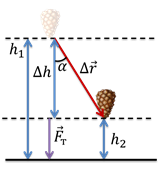
Наконец, рассмотрим случай, когда между направлением силы тяжести и перемещением существует произвольный угол α.
Обозначим модуль перемещения за s. В этом случае, работа силы тяжести равна:
Но, исходя из определения косинуса:
Таким образом, мы в третий раз получили одинаковый результат.
Более того, если даже мы рассмотрим криволинейную траекторию, то убедимся, что результат будет тем же.
Любую кривую мы можем представить в виде ломаной линии, состоящей из очень маленьких горизонтальных и вертикальных отрезков. На горизонтальных отрезках работа силы тяжести будет равна нулю, поскольку в этом случае направление перемещения перпендикулярно направлению силы тяжести. На вертикальных участках работа будет равна: A = mg(s1 + … + sn). Очевидно, что эта сумма будет равна (h1 – h2):
Таким образом, мы убедились, что работа силы тяжести не зависит от траектории движения тела. Имеет значение лишь то, насколько начальное положение тела отличается от конечного. Это плавно подводит нас к понятию потенциальной энергии, которое мы рассмотрим немного позже.
Из приведенных примеров вытекает еще один важный вывод: при движении тела по замкнутой траектории работа силы тяжести равна нулю. Для начала рассмотрим контур, имеющий форму прямоугольника. Как мы уже убедились, при движении тела в горизонтальном направлении, работа силы тяжести равна нулю. Вектор перемещения направлен перпендикулярно вектору силы тяжести. При перемещении же по противолежащим вертикальным сторонам контура, сила тяжести совершает работу, равную по абсолютной величине, но противоположную по знаку.
В одном случае вектор перемещения направлен так же, как вектор силы тяжести, а в другом — направлен в противоположную сторону. Это довольно логично, поскольку при движении тела вниз, сила тяжести ему «помогает», а при движении вверх — наоборот, мешает.
Мы можем сколь угодно усложнить эту траекторию, получив совершенно произвольный замкнутый контур.
Но опять же, разбив все кривые на ломаные линии с горизонтальными и вертикальными участками, мы убедимся, что суммарная работа будет равна нулю.
Силы, обладающие такими свойствами, называются консервативными. То есть, консервативная сила — это такая сила, работа которой в замкнутом контуре равна нулю.
Примеры решения задач.
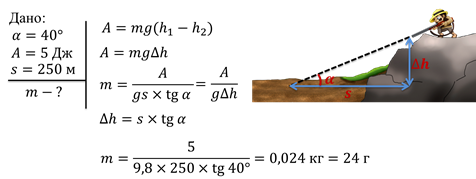
Задача 1. Охотник стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы, то какова её масса?
Задача 2. Находясь на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна 5 кг, то каково ускорение свободного падения на Нептуне?
Источник
Конспект Работа силы тяжести
Работа силы тяжести. Решение задач
Цель урока: определить формулу для работы силы тяжести; определить, что работы силы тяжести не зависит от траектории движения тела; развить практические навыки по решению задач.
1.Организационный момент. Приветствие учащихся, проверка отсутствующих, постановка цели урока.
2.Проверка домашней работы.
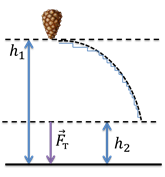
3.Изучение нового материала. На предыдущем уроке мы с вами определили формулу для определения работы. Какой формулой определяется работа постоянной силы? (А= FScosα )
Что такое А и S ?
Теперь же применим эту формулу для силы тяжести. Но для начала вспомним, чему равна сила тяжести? ( F = mg )
Рассмотрим случай а) тело падает вертикально вниз. Как мы с вами знаем сила тяжести всегда направленно строго вниз. Для того чтобы определить направление S необходимо вспомнить определение. (Перемещение-это вектор соединяющий начальную и конечную точку. Направлен он от начала к концу) 
Т.о. для определения 
, Так как направление перемещения и силы тяжести совпадают, то α =0 и работа силы тяжести равна: 
Рассмотрим случай б) тело двигается вертикально вверх. Т.к. направление силы тяжести и перемещении противоположны, то то α =0 и работа силы тяжести равна 
. 
Т.о. образом если сравнить две формулы по модулю, то они будут одинаковы.
Рассмотрим случай в) тело движется по наклонной плоскости. Работа силы равна скалярному произведению вектора силы на вектор перемещения тела, совершённого под действием данной силы, то есть работа сила тяжести в данном случае будет равна 
, где 
– угол между векторами силы тяжести и перемещения. На рисунке видно, что перемещение ( 
) представляет собой гипотенузу прямоугольного треугольника, а высота h – катет. Согласно свойству прямоугольного треугольника: 
.Следовательно 
Т.о. какой можно сделать вывод? (что работа силы тяжести не зависит от траектории движения.)
Рассмотрим последний пример, когда траектория движения будет замкнутая линия. Кто скажет чему будет равна работа и почему? (А=0, т.к. перемещение равно 0) 
Отметим!: работа силы тяжести при движении тела по замкнутой траектории равна нулю.
4. Закрепление материала.
Задача 1. Охотник стреляет со скалы под углом 40° к горизонту. За время падения пули работа силы тяжести составила 5 Дж. Если пуля вошла в землю на расстоянии 250 м от скалы, то какова её масса?
Задача 2. Находясь на Нептуне, тело совершило перемещение так, как показано на рисунке. При этом перемещении работа силы тяжести составила 840 Дж. Если масса данного тела равна 5 кг, то каково ускорение свободного падения на Нептуне?
Источник
Способ определения работы силы тяжести
«Физика — 10 класс»
Вычислим работу силы тяжести при падении тела (например, камня) вертикально вниз.
В начальный момент времени тело находилось на высоте hx над поверхностью Земли, а в конечный момент времени — на высоте h2 (рис. 5.8). Модуль перемещения тела |Δ
| = h1 — h2.
Направления векторов силы тяжести 
T и перемещения Δ совпадают. Согласно определению работы (см. формулу (5.2)) имеем
А = |Т| |Δ|cos0° = mg(h1 — h2) = mgh1 — mgh2. (5.12)
Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h1 над поверхностью Земли, и оно достигло высоты h2 (рис. 5.9). Векторы Т и Δ направлены в противоположные стороны, а модуль перемещения |Δ| = h2 — h1. Работу силы тяжести запишем так:
А = |Т| |Δ|cos180° = -mg(h2 — h1) = mgh1 — mgh2. (5.13)
Если же тело перемещается по прямой так, что направление перемещения составляет угол а с направлением силы тяжести (рис. 5.10), то работа силы тяжести равна:
А = |Т| |Δ|cosα = mg|BC|cosα.
Из прямоугольного треугольника BCD видно, что |BC|cosα = BD = h1 — h2. Следовательно,
Это выражение совпадает с выражением (5.12).
Формулы (5.12), (5.13), (5.14) дают возможность подметить важную закономерность. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела, определяемых высотами h1 и h2 над поверхностью Земли.
Более того, работа силы тяжести при перемещении тела массой т из одного положения в другое не зависит от формы траектории, по которой движется тело. Действительно, если тело перемещается вдоль кривой ВС (рис. 5.11), то, представив эту кривую в виде ступенчатой линии, состоящей из вертикальных и горизонтальных участков малой длины, увидим, что на горизонтальных участках работа силы тяжести равна нулю, так как сила перпендикулярна перемещению, а сумма работ на вертикальных участках равна работе, которую совершила бы сила тяжести при перемещении тела по вертикальному отрезку длиной h1 — h2. Таким образом, работа силы тяжести при перемещении вдоль кривой ВС равна:
Работа силы тяжести не зависит от формы траектории, а зависит только от положений начальной и конечной точек траектории.
Определим работу А при перемещении тела по замкнутому контуру, например по контуру BCDEB (рис. 5.12). Работа А1 силы тяжести при перемещении тела из точки В в точку D по траектории BCD: А1 = mg(h2 — h1), по траектории DEB: А2 = mg(h1 — h2).
При движении тела по замкнутой траектории работа силы тяжести равна нулю.
Итак. работа силы тяжести не зависит от формы траектории тела; она определяется лишь начальным и конечным положениями тела. При перемещении тела по замкнутой траектории работа силы тяжести равна нулю.
Силы, работа которых не зависит от формы траектории точки приложения силы и по замкнутой траектории равна нулю, называют консервативными силами.
Сила тяжести является консервативной силой.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Источник
