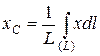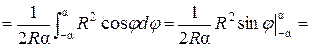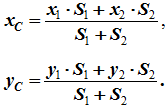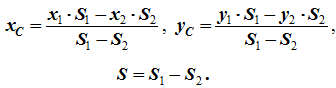Способы определения координат центров тяжести тел
Основываясь на полученных формулах, можно предложить практические способы определения центров тяжести тел.
1. Симметрия. Если однородное твердое тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит, соответственно, в данной плоскости, оси или центре.
2. Разбиение. Для тел, состоящих из простых по форме тел, используется способ разбиения. Тело разбивается на части, центр тяжести которых находится методом симметрии. Центр тяжести всего тела определяется по формулам центра тяжести объема (площади).
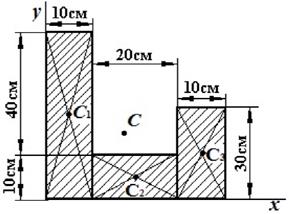
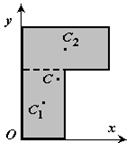
Пример. Определить координаты центра тяжести пластины, изображенной на рис. 6.3.
Решение: Для нахождения центра тяжести пластины разбиваем ее на три прямоугольника и отмечает центры тяжести каждого из них: C1, C2 и C3. Затем определяем координаты центров тяжести каждого прямоугольника и их площади:
Тогда координаты центра тяжести пластины, согласно формулам из раздела 6.2, будут равны:
см; 
см.
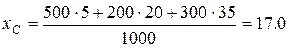
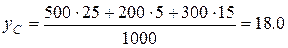
Ответ: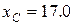 
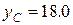
см; 
см.
3. Дополнение. Этот способ является частным случаем способа разбиения. Он используется, когда тело имеет вырезы, срезы и др., если координаты центра тяжести тела без выреза известны.
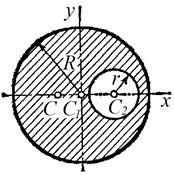
Пример. Определить центр тяжести круглой пластины, имеющей вырез радиусом r = 0,6 R (рис. 6.4).
Решение: Круглая пластина имеет центр симметрии. Поместим начало координат в центре пластины O1. Площадь пластины без выреза S1= πR 2 ,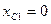 
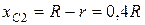
, площадь выреза S2 = πr 2 = π0,36R 2 . Площадь пластины с вырезом S2 = =πR 2 (1 — 0,36)= 0,64πR 2 ; 
.
Пластина с вырезом имеет ось симметрию О1x, следовательно, yc=0.
.
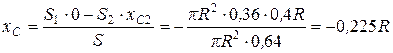
4. Интегрирование. Если тело нельзя разбить на конечное число частей, положение центров тяжести которых известны, тело разбивают на произвольные малые объемы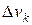 
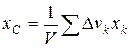
, для которых формула с использованием метода разбиения принимает вид: 
.
Далее переходят к пределу, устремляя элементарные объемы к нулю, т.е. стягивая объемы в точки. Суммы заменяют интегралами, распространенными на весь объем тела, тогда формулы определения координат центра тяжести объема принимают вид:
; 
; 
.
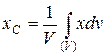
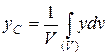
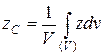
Аналогично, формулы для определения координат центра тяжести площади:
; 
.
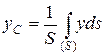
Формулы для определения положения центра тяжести линии имеют вид:
; 
; 
.
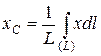
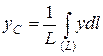
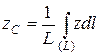
Координаты центра тяжести площади необходимо определять при изучении равновесия пластинок, при вычислении интеграла Мора в строительной механике.
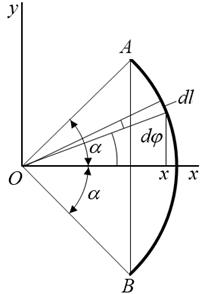
Пример. Определить центр тяжести дуги окружности радиуса R с центральным углом АОВ = 2α (рис. 6.5).
Решение: Дуга окружности симметрична оси Ох, следовательно, центр тяжести дуги лежит на оси Ох, yс = 0. Выделим на дуге AB элемент длиной 
, положение которого определяется углом j. Координата x этого элемента будет равна 
.
Тогда, согласно формуле определения центра тяжести линии, получим:
,
где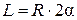 
– длина дуги AB.
6. Экспериментальный способ. Центры тяжести неоднородных тел сложной конфигурации можно определять экспериментально: методом подвешивания и взвешивания. Первый способ состоит в том, что тело подвешивается на тросе за различные точки. Направление троса на котором подвешено тело, будет давать направление силы тяжести. Точка пересечения этих направлений определяет центр тяжести тела.
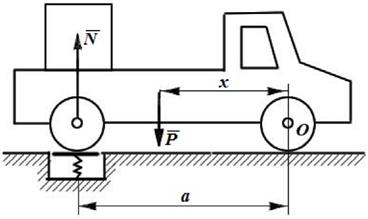
Метод взвешивания состоит в том, что сначала определяется вес тела, например автомобиля. Затем на весах определяется давление заднего моста автомобиля на опору. Составив уравнение равновесия относительно какой- либо точки, например оси передних колес, можно вычислить расстояние от этой оси до центра тяжести автомобиля (рис. 6.6).
; 
; 
.
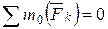
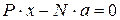
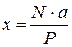
Иногда при решении задач следует применять одновременно разные методы определения координат центра тяжести.
Источник
Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz , где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆Vi , то на каждую его часть будет действовать сила притяжения ∆Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
Рис.1. Параллельная система сил
Центром тяжести твердого тела называется центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.2. Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сплошной сложной геометрической фигуры по оси x;
— координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей. Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
Рис.4. Центр тяжести сложной геометрической фигуры,
— центр тяжести и площадь первой фигуры;
— центр тяжести и площадь второй фигуры;
— координата центра тяжести сложной геометрической фигуры по оси x;
— координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3) ; yc =1/3(y1+y2+y3).
Рис.5. Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2 ; yc =h/2.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2 ; yc =4R/3π.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R ; yc =R.
Рис. 8. Центр тяжести круга
Вопросы для самопроверки:
— Что называется центром параллельных сил?
— Что называется центром тяжести тела?
— Почему силы притяжения Земле, действующие на точку тела, можно принять за систему параллельных сил?
— Запишите формулу для определения положения центра тяжести неоднородных и однородных тел, формулу для определения положения центра тяжести плоских сечений?
— Запишите формулу для определения положения центра тяжести простых геометрических фигур: прямоугольника, квадрата, трапеции и половины круга?
— Как используются свойства симметрии при определении центров тяжести тел?
— В чем состоит сущность способа отрицательных площадей?
— Каким графическим построением можно найти центр тяжести треугольника?
— Запишите формулу, определяющую центр тяжести треугольника.
Источник
iSopromat.ru
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел.
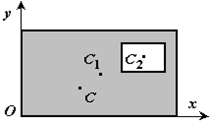
Разбиение. Тело разбивается на конечное число частей, для каждой из которых положение центра тяжести C и площадь S известны. Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями S1 и S2 (S = S1+ S2). Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны: 
Дополнение (Метод отрицательных площадей или объемов).
Частный случай способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9): 
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
