Способ определения гравитационной постоянной

Учёные смущённо признают, что до сих пор не знают точной величины гравитационного взаимодействия

По легенде, первый эксперимент, показавший, что все объекты падают с одной скоростью, вне зависимости от массы, провёл Галилео Галилей, стоя на вершине Пизанской башни. Два любых объекта, брошенных вниз в гравитационном поле, в отсутствии сопротивления воздуха (или при пренебрежении им) будут ускоряться одинаково. Позже это правило было кратко записано Ньютоном после изучения им данного вопроса.

Впервые начав формулировать законы физики, мы делали это эмпирически: посредством экспериментов. Бросьте шар с башни, как это, возможно, сделал Галилей, и вы сможете измерить, сколько он пролетит и через какое время упадёт. Отпустите маятник, и вы сможете обнаружить взаимосвязь между его длиной и количеством времени на один период. Проделав это с различными расстояниями, длинами и временными отрезками, вы начнёте замечать систему: высота падения объекта пропорциональна квадрату времени, период маятника пропорционален квадратному корню его длины.

Но чтобы превратить пропорции в уравнения, нужно подобрать одну константу.

Орбиты планет внутренней Солнечной системы не идеально круглые, но близки к окружностям. Меркурий и Марс дальше всего отклоняются от идеала, демонстрируя эллиптичность орбит. В середине XIX века учёные начали замечать отклонения Меркурия от предсказаний Ньютоновской гравитации, которые смогла объяснить только Общая теория относительности в XX веке. Один и тот же закон гравитации, и одна и та же константа, описывают воздействие гравитации на всех масштабах, от Земли до космоса.

В этих примерах, и во многих других, в роли константы пропорциональности выступает G, гравитационная постоянная. Луна движется вокруг Земли, планеты – вокруг Солнца, свет искажается гравитационным линзированием, кометы теряют энергию, убегая из Солнечной системы – и всё это происходит пропорционально G. Ещё до Ньютона, в 1640-х и 1650-з итальянские учёные Франческо Гримальди и Джованни Риччоли выполнили первые расчёты гравитационной постоянной, что означает, что она стала первой из всех определённых фундаментальных констант, опередив даже определение скорости света в 1676 году, выполненное Оле Рёмером.

Ньютоновский закон всемирного тяготения заменила Общая теория относительности Эйнштейна. Он основывался на мгновенном дальнодействии и был чрезвычайно прямолинеен. Величина гравитационной постоянной G из этого уравнения до сих пор известна очень плохо.

Если взять две массы во Вселенной и разместить их вблизи друг друга, они будут притягиваться. Согласно законам Ньютона, действующим для всех масс, кроме чрезвычайно больших, и для всех небольших расстояний, сила тяготения связана с обеими массами, разделяющим их расстоянием и гравитационной постоянной G. Несколько веков мы уточняли наши измерения множества фундаментальных констант до невероятной точности. Скорость света c известна точно: 299,792,458 м/с. Постоянная Планка ħ, управляющая квантовыми взаимодействиями, имеет значение 1,05457180 × 10 -34 Дж*с, с погрешностью в ± 0,000000013 × 10 -34 Дж*с.

Но с G выходит совершенно другое дело.

Используем ли мы описание гравитации от Ньютона или Эйнштейна, величина силы определяется, в частности, величиной гравитационной постоянной G, чьё значение приходится измерять экспериментально, и нельзя вывести из других.

В 1930-х для значения G было получено 6,67 × 10 -11 Н*м 2 /кг 2 , в 1940-х её уточнили до 6,673 × 10 -11 Н*м 2 /кг 2 , причём оба измерения проделал Пол Хейл. Как можно было ожидать, со временем значения постоянно улучшались, а погрешность падала с 0,1% до 0,04%, и дошла до 0,012% в конце 1990-х благодаря работам Барри Тэйлора из NIST.

Если взглянуть на старую копию буклета данных по частицам, в котором приводились значения фундаментальных констант, то там можно найти значение G, равное 6,67259 × 10 -11 Н*м 2 /кг 2 , с погрешностью всего в 0,00085 × 10 -11 Н*м 2 /кг 2 .

Значения фундаментальных констант на 1998 год

А затем произошло нечто забавное.

Позже в том году проведенные эксперименты обнаружили значение, бывшее слишком высоким для указанной величины: 6,674 × 10 -11 Н*м 2 /кг 2 . Разные команды, использовавшие разные методы, получали значения G, не совпадавшие друг с другом на 0,15%, что больше, чем в десять раз превышает погрешность, о которой сообщали ранее.

Как это произошло?

Первоначальный эксперимент по точному измерению G, разработанный и опубликованный Генри Кавендишем, основывается на принципе крутильных весов, крутящихся в зависимости от гравитационного притяжения недалеко расположенной массы хорошо известной величины.

Первое точное измерение гравитационной постоянной, не зависящее от других неизвестных (к примеру, от массы Солнца или массы Земли) состоялось только в эксперименте Генри Кавендиша в конце XVIII века. Кавендиш разработал эксперимент, известный, как крутильные весы, в котором небольшая гантель была подвешена и идеально сбалансирована на проводе. Рядом с каждой из масс на конце гантели располагались две массы побольше, гравитационно притягивавшие небольшие массы. Величина поворота гантели при известных расстояниях и массах давала нам возможность измерить G экспериментально.

Несмотря на множество прорывов в физике за последние 200 с лишним лет, в экспериментах по измерению G используется тот же принцип, что использовался в эксперименте Кавендиша. Вплоть до сегодняшнего дня никакая другая техника измерения или устройство эксперимента не дали лучших результатов.

Есть подозрение, что одной из причин расхождений служит хорошо известный психологический фактор предвзятости подтверждения. Если все ваши коллеги получают результат вида 6,67259 × 10 -11 Н*м 2 /кг 2 , разумно ожидать, что и вы получите результат типа 6,67224 × 10 -11 Н*м 2 /кг 2 , или 6,67293 × 10 -11 Н*м 2 /кг 2 ; но если вы получаете что-то вроде 6,67532 × 10 -11 Н*м 2 /кг 2 , вы решите, что сделали что-то не так.

Вы будете искать источники ошибки, пока не найдёте. Вы будете снова и снова повторять эксперимент, пока не получите нечто разумное: что-то, не противоречащее величине 6,67259 × 10 -11 Н*м 2 /кг 2 .

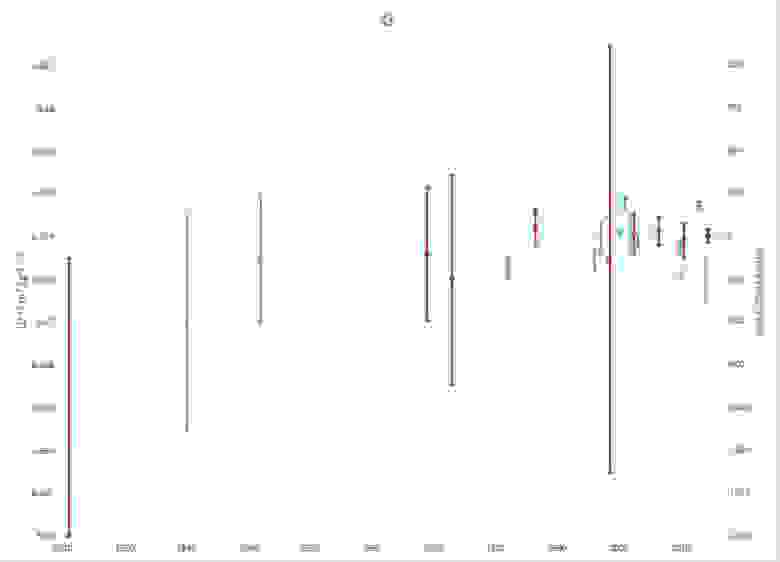
В 1997 году команда Бэгли и Лютера провела эксперимент с крутильными весами, давший результат в 6,674 × 10 -11 Н*м 2 /кг 2 , который приняли достаточно серьёзно для того, чтобы подвергнуть сомнению предыдущую погрешность измерений G

Поэтому таким шоком стало событие 1998 года, когда очень тщательно работающая команда получила результат, отличающийся на невероятные 0,15% от предыдущих, в то время как заявленные погрешности предыдущих измерений были в десять раз меньше этого. NIST в ответ отвергла предыдущие погрешности, и полученные значения урезали до четырёх значимых цифр, а погрешность увеличили.

Крутильные весы и крутильные маятники, сделанные под влиянием первоначального эксперимента Кавендиша, продолжают лидировать в измерениях G, опережая более современные технологии атомной интерферометрии. Только в этом августе китайская команда заявила о получении наиболее точного значения G из двух независимых измерений: 6,674184 × 10 -11 Н*м 2 /кг 2 и 6,674484 × 10 -11 Н*м 2 /кг 2 с погрешностями в 0,0011%.

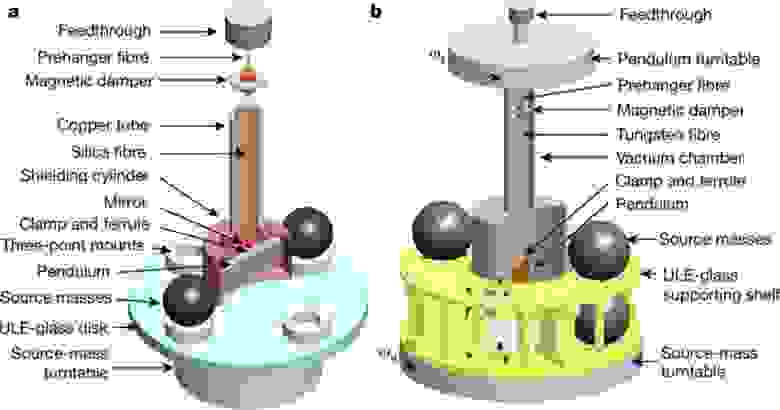
Две экспериментальные установки, схемы которых были опубликованы в августе 2018 в журнале Nature, дали наиболее точные (по заявлению учёных) значения для G

Эти значения согласуются друг с другом в пределах двух среднеквадратичных отклонений, но не согласуются с другими измерениями, сделанными другими командами за 15 последних лет, разнящимися от 6,6757 × 10 -11 Н*м 2 /кг 2 до 6,6719 × 10 -11 Н*м 2 /кг 2 . В то время, как другие фундаментальные константы известны с точностью от 8 до 14 значимых цифр, при измерении G погрешности получаются в тысячи или миллиарды раз большими.

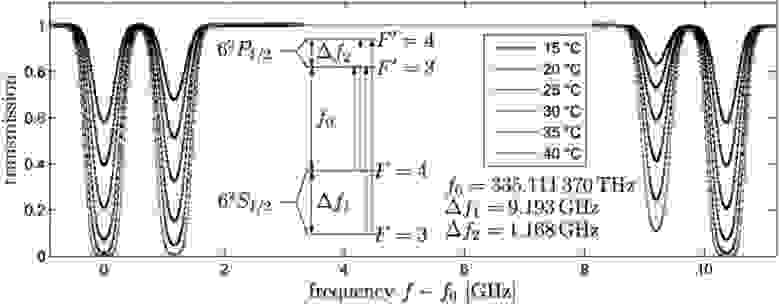
Атомный переход с орбитали 6S, Delta_f1, определяет метр, секунду и скорость света. Точность определения квантовых констант в тысячи раз превышает точность измерения G, первой из измеренных констант.

Гравитационная постоянная Вселенной, G, была первой из измеренных. Однако же, спустя 350 лет после первого измерения, стыдно констатировать, насколько плохо она известна по сравнению со всеми другими. Мы используем эту константу в огромном количестве измерений и расчётов, от гравитационных волн до пульсаров, отмеряющих расширение Вселенной. И всё же наша возможность определять её основывается на мелкомасштабных экспериментах, проводимых на Земле. В наши попытки измерить её проникают крохотные источники неопределённости, от плотности материалов до сейсмических колебаний. И пока мы не сумеем достичь большего, везде, где важна гравитация, будет присутствовать внутренняя, неприятно большая погрешность. На дворе 2018 год, а мы всё ещё не знаем, насколько велика на самом деле гравитация.

Больше статей на научно-популярную тему вы сможете найти на сайте Golovanov.net. Читайте: необходима ли тектоника плит для образования жизни на планете; откуда берётся энергия в тёмной энергии; не приведёт ли деятельность человека к межзвёздной войне; существует ли полезное для здоровья количество алкоголя; серию статей по космологии «Спросите Итана».

Не стесняемся поддерживать проект материально (банковские карты, яндекс.деньги, вебмани, биткоины, да как угодно). Спасибо всем, кто уже оказал поддержку!

Источник

Все самое интересное что нужно знать о гравитационной постоянной

В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.

Что такое и чему равна гравитационная постоянная

Формула закона всемирного тяготения, известная по курсу школьной механики:

G – коэффициент пропорциональности или гравитационная постоянная;

m_1, m₂ – массы двух тел, испытывающих взаимное притяжение;

r – расстояние между ними.

Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

В чём измеряется гравитационная постоянная

Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной – , но её возникновение легко объясняется.

Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.

После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.

То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.

Проведём математические вычисления самостоятельно.

Нужно уравнять и .

Для этого нужно разделить на 1с 2 и 1кг, а также умножить на м 3 , получим:

Получилась требуемая размерность.

Следовательно, постоянная имеет размерность .

Как найти гравитационную постоянную – история открытия

Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.

Работы Ньютона

При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.

Вместо известной сегодня постоянной присутствовал гравитационный параметр:

M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.

Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.

• для Земли ;
• Луны ;
• Солнца .

Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.

Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша

Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.

Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.

Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.

В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.

Измерение гравитационной постоянной

Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно , а Олег Павлович Спиридонов в сборнике постоянных приводит значение .

Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение

с относительной погрешностью 5*10 -3 .

Современная история изменений гравитационной постоянной

Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

По результатам команды первый метод продемонстрировал значение гравитационной постоянной , второй метод – . Относительная погрешность составила 11,6*10 -6

Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.

Источник