Магнитное поле соленоида. Формула, суть явления.
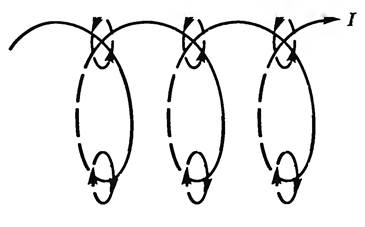
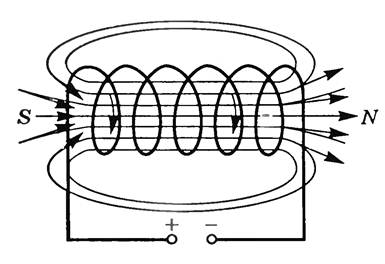
Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков.
Давайте рассмотрим магнитную индукцию, создаваемую каждым витком. Видно, что индукция внутри каждого витка направлена в одну и ту же сторону. Если смотреть в центр витка, то индукция от его краев будет складываться. При этом индукция магнитного поля между двух соседних витков направлена встречно. Так как она создана одним и тем же током то она компенсируется.
Если витки соленоида намотаны достаточно плотно, то между всеми витками встречное поле будет компенсировано, а внутри витков произойдет сложение отдельных поле в одно общее. Линии этого поля будут проходить внутри соленоида, и охватывать его снаружи.
Если исследовать магнитное поле внутри соленоида любыми способами, например, с помощью железных опилок то можно сделать вывод, что оно однородно. Лини магнитного поля в этой области представляют собой параллельные прямые. Мало того что они параллельны сами себе но они еще параллельны оси соленоида. Выходя за приделы соленоида, они искривляются и замыкаются снаружи катушки.
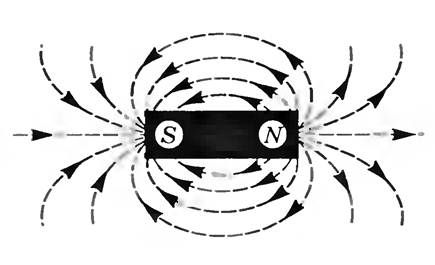
Из рисунка видно, что поле создаваемое соленоидом похоже на поле, которое создает постоянный стержневой магнит. На одном конце силовые линии выходят из соленоида и этот конец аналогичен северному полюсу постоянного магнита. А в другой они входят, и этот конец соответствует южному полюсу. Отличие же заключается в том, что поле присутствует и внутри соленоида. И если провести опыт с железными опилками, то они втянутся в пространство между витками.
Но если внутрь соленоида вставить деревянный сердечник либо сердечник из любого другого немагнитного материала, то при проведении опыта с железной стружкой картина поля постоянного магнита и соленоида будет идентична. Так как деревянный сердечник не исказит силовые лини, но при этом не даст проникнуть опилкам внутрь катушки.
Для определения полюсов соленоида можно использовать несколько методов. Например, самый простой, использовать магнитную стрелку. Она притянется к противоположному полюсу магнита. Если же известно направление тока в витке полюсы можно определить при помощи правила правого винта. Если вращать головку правого винта в направлении тока, то поступательное движение укажет направление поля в соленоиде. А зная, что поле направлено от северного полюса к южному и можно определить, где какой полюс находится.
Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.
Где N число витков соленоида
l длинна соленоида
n число витков на единицу длинны
I Ток в соленоиде
Мю магнитная проницаемость среды находящейся внутри соленоида
Источник
Способ определения энергии магнитного поля соленоида
Применим теорему о циркуляции вектора 
для вычисления простейшего магнитного поля – бесконечно длинного соленоида, представляющего собой тонкий провод, намотанный плотно виток к витку на цилиндрический каркас (рис. 2.11).
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно длинный соленоид симметричен любой, перпендикулярной к его оси плоскости. Взятые попарно (рис. 2.12), симметричные относительно такой плоскости витки создают поле, в котором вектор перпендикулярен плоскости витка, т.е. линии магнитной индукции имеют направление параллельное оси соленоида внутри и вне его.
Из параллельности вектора оси соленоида вытекает, что поле как внутри, так и вне соленоида должно быть однородным.
Возьмём воображаемый прямоугольный контур 1–2–3–4–1 и разместим его в соленоиде, как показано на рисунке 2.13.
Второй и четвёртый интегралы равны нулю, т.к. вектор перпендикулярен направлению обхода, т.е 
.
Возьмём участок 3–4 – на большом расстоянии от соленоида, где поле стремится к нулю; и пренебрежём третьим интегралом, тогда
где 
– магнитная индукция на участке 1–2 – внутри соленоида, 
– магнитная проницаемость вещества.
Если отрезок 1–2 внутри соленоида, контур охватывает ток:
где n – число витков на единицу длины, I – ток в соленоиде (в проводнике).
Тогда магнитная индукция внутри соленоида:
 , | (2.7.1) |
и 
, т.е. 
.
Бесконечно длинный соленоид аналогичен плоскому конденсатору – и тут, и там поле однородно и сосредоточено внутри.
Произведение nI – называется число ампер витков на метр.
У конца полубесконечного соленоида, на его оси магнитная индукция равна:
 , | (2.7.2) |
Практически, если длина соленоида много больше, чем его диаметр, формула (2.7.1) справедлива для точек вблизи середины, формула (2.7.2) для точек около конца.
Если же катушка короткая, что обычно и бывает на практике, то магнитная индукция в любой точке А, лежащей на оси соленоида, направлена вдоль оси (по правилу буравчика) и численно равна алгебраической сумме индукций магнитных полей создаваемых в точке А всеми витками. В этом случае имеем:
· В точке, лежащей на середине оси соленоида магнитное поле будет максимальным:
 , | (2.7.3) |
где L – длина соленоида, R – радиус витков.
· В произвольной точке конечного соленоида (рис. 2.14) магнитную индукцию можно найти по формуле
 , | (2.7.4) |
На рисунке 2.15 изображены силовые линии магнитного поля : а) металлического стержня; б) соленоида; в) железные опилки, рассыпанные на листе бумаги, помещенной над магнитом, стремятся вытянуться вдоль силовых линий; г) магнитные полюсы соленоида.
Источник
Магнитное поле соленоида
Соленоидом называют катушку цилиндрической формы из проволоки, витки которой намотаны вплотную в одном направлении, а длина катушки значительно больше радиуса витка.
Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке 3 видно, что внутри соленоида линии магнитной индукции каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление.
Поэтому при достаточно плотной намотке соленоида противоположно направленные участки линий магнитной индукции соседних витков взаимно уничтожаются, а одинаково направленные участки сольются в общую линию магнитной индукции, проходящую внутри соленоида и охватывающую его снаружи. Изучение этого поля с помощью опилок показало, что внутри соленоида поле является однородным, магнитные линии представляют собой прямые линии, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида (рис. 4).
Нетрудно заметить сходство между магнитным полем соленоида (вне его) и магнитным полем постоянного стержневого магнита (рис. 5). Конец соленоида, из которого магнитные линии выходят, аналогичен северному полюсу магнита N, другой же конец соленоида, в который магнитные линии входят, аналогичен южному полюсу магнита S.
Полюсы соленоида с током на опыте легко определить с помощью магнитной стрелки. Зная же направление тока в витке, эти полюсы можно определить с помощью правила правого винта: вращаем головку правого винта по току в витке, тогда поступательное движение острия винта укажет направление магнитного поля соленоида, а следовательно, и его северного полюса. Модуль магнитной индукции внутри однослойного соленоида вычисляется по формуле
B = μμ 0 NI l = μμ 0 nl,
где Ν — число витков в соленоиде, I — длина соленоида, n — число витков, приходящееся на единицу длины соленоида.
| Намагничивание магнетика. Вектор намагниченности. | |||||||
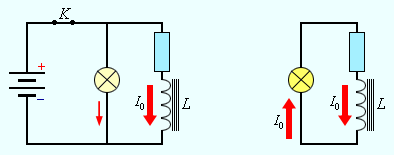
Если по проводнику течет ток, то вокруг проводника создаётся МП. Мы пока рассматривали провода, по которым текли токи, находящиеся в вакууме. Если провода, несущие ток, находятся в некоторой среде, то м.п. изменяется. Это объясняется тем, что под действием м.п. всякое вещество способно приобретать магнитный момент, или намагничиваться (вещество становится магнетиком). Вещества, намагничивающиеся во внешнем м.п. против направления поля называются диамагнетиками. Вещества, слабо намагничивающиеся во внешнем м.п. по направлению поля называются парамагнетиками Намагниченное в-во создаёт м.п. –  , это м.п. накладывается на м.п., обусловленное токами –  . Тогда результирующее поле:
Истинное (микроскопическое) поле в магнетике сильно изменяется в пределах межмолекулярных расстояний. Для объяснения намагничения тел Ампер предположил, что в молекулах вещества циркулируют круговые микроскопические токи, обусловленные движением электронов в атомах и молекулах. Каждый такой ток обладает магнитным моментом и создаёт в окружающем пространстве м.п. Если внешнее поле отсутствует, то молекулярные токи ориентированы беспорядочным образом, и обусловленное ими результирующее поле равно 0. Намагниченностью называют векторную величину, равную магнитному моменту единицы объёма магнетика:
где Суммирование производится по всем молекулам, заключённым в объёме Намагниченность можно представить так: Токи намагничивания I’ . Намагничивание вещества связано с преимущественной ориентацией магнитных моментов отдельных молекул в одном направлении. Элементарные круговые токи, связанные с каждой молекулой, называются молекулярными. Молекулярные токи оказываются ориентированными, т.е. возникают токи намагничивания — Токи, текущие по проводам, вследствие движения в веществе носителей тока называют токами проводимости —
Для электрона движущегося по круговой орбите по часовой стрелке; ток направлен против часовой стрелки и Циркуляция вектора намагниченности Дифференциальная форма записи теоремы о циркуляции вектора
Дифференциальная форма записи теоремы о циркуляции — формула (54.7) – ротор вектора Напряжённость магнитного поля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. В СИ: В СГС: В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ0μ H в системе СИ (см. Магнитная проницаемость, также см. Магнитная восприимчивость). В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр. 1 Э = 1000/(4π) А/м ≈ 79,5775 А/м. 1 А/м = 4π/1000 Э ≈ 0,01256637 Э. Физический смыслВ вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряжённость магнитного поля совпадает с вектором магнитной индукции с точностью до коэффициента, равного 1 в СГС и μ0 в СИ. В магнетиках (магнитных средах) напряжённость магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ , что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было». Например, если поле создаётся катушкой с током, в которую вставлен железный сердечник, то напряжённость магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ — с точностью до постоянного размерного коэффициента) с вектором B0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, без всякой дополнительной информации о материале сердечника и его магнитных свойствах. При этом надо иметь в виду, что более фундаментальной характеристикой магнитного поля является вектор магнитной индукции B. Именно он определяет силу действия магнитного поля на движущиеся заряженные частицы и токи, а также может быть непосредственно измерен, в то время как напряжённость магнитного поля H можно рассматривать скорее как вспомогательную величину (хотя рассчитать её, по крайней мере, в статическом случае, проще, в чём и состоит её ценность: ведь H создают так называемые свободные токи, которые сравнительно легко непосредственно измерить, а трудно измеримые связанные токи — то есть токи молекулярные и т. п. — учитывать не надо). Правда, в обычно используемое выражение для энергии магнитного поля (в среде) B и H входят почти равноправно, но надо иметь в виду, что в эту энергию включена и энергия, затраченная на поляризацию среды, а не только энергия собственно поля. Энергия магнитного поля как такового выражается только через фундаментальное B. Тем не менее видно, что величина H феноменологически и тут весьма удобна. Виды магнетиков Диамагнетики имеют магнитную проницаемость чуть меньше 1. Отличаются тем, что выталкиваются из области магнитного поля. Парамагнетики имеют магнитную проницаемость чуть более 1. Подавляющее количество материалов являются диа- и пара- магнетиками. Ферромагнетики обладают исключительно большой магнитной проницаемостью, доходящей до миллиона. По мере усиления поля проявляется явление гистерезиса, когда при увеличении напряженности и при последующем уменьшении напряженности значения В(Н) не совпадают друг с другом. В литературе различают несколько определений магнитной проницаемости. Начальная магнитная проницаемость mн — значение магнитной проницаемости при малой напряженности поля. Максимальная магнитная проницаемость mmax — максимальное значение магнитной проницаемости, которое достигается обычно в средних магнитных полях. Из других основных терминов, характеризующих магнитные материалы, отметим следующие. Намагниченность насыщения — максимальная намагниченность, которая достигается в сильных полях, когда все магнитные моменты доменов ориентированы вдоль магнитного поля. Петля гистерезиса — зависимость индукции от напряженности магнитного поля при изменении поля по циклу: подъем до определенного значения — уменьшение, переход через нуль, после достижения того же значения с обратным знаком — рост и т.п. Максимальная петля гистерезиса — достигающая максимальной намагниченности насыщения. Остаточная индукция Bост — индукция магнитного поля на обратном ходе петли гистерезиса при нулевой напряженности магнитного поля. Коэрцитивная сила Нс — напряженность поля на обратном ходе петли гистерезиса при которой достигается нулевая индукция.
|
.
,
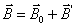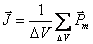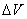— физически бесконечно малый объём, взятый в окрестности рассматриваемой точки; 
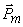— магнитный момент отдельной молекулы.
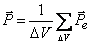где,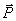 
— поляризованность диэлектрика , 
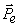— дипольный элемент 
).
.
.
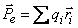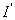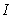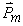по правилу правого винта направлен вертикально вверх.
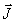по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром Г.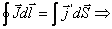
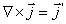
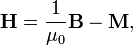где 
— магнитная постоянная.
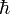), тогда электроны, протоны и нейтроны имеют спин равный ½ 
