Способ образования непосредственных умозаключений

Непосредственное умозаключение

Умозаключение – форма мышления, посредством которой из одного и более суждений (исходных посылок) по определенным правилам получают новое знание, называемое выводным.

Элементы структуры умозаключения:

1. 1. Посылки – это суждения, из которых делается вывод.
   2. Заключение – это суждение, выводимое из посылок.
   3. Логическая связь между посылками и заключением.

Различают виды умозаключений по следующим основаниям:

1. по степени достоверности вывода:
   • Логически необходимые (достоверные) умозаключения, которые да­ют истинные выводы. К ним относятся дедукция, полная индукция, строгая аналогия.
   • Вероятные (правдоподобные) умозаключения, которые дают вероят­ные виды. К ним относятся неполная индукция, нестрогая аналогия.
2. по направлению движения мысли:
   • Дедукция (от лат. deductio – выведение) – умозаключение от общего к частному.
   • Индукция (от лат. induction – наведение) – умозаключение от частного к общему.
   • Аналогия (от греч. analogia – соответствие) – умозаключение, принцип мышления которого направлен от мысли к мысли одинаковой степени общности.

Непосредственным называют дедуктивное умозаключение, в котором вывод делается из одной посылки путем ее преобразования.

Виды непосредственных умозаключений:

1. 1. превращение,
   2. обращение,
   3. преобразование по логическому квадрату.

При помощи операций превращения, обращения (а также производных от них — противопоставление субъекту и противопоставление предикату) получаются новые суждения, которые будут эквивалентными исходным.

Превращение

Превращение — это дедуктивное умозаключение, в результате которого связка исходного суждения меняется на противоположную и предикат исходного суждения меняется на противоположный.

Данный вид умозаключения подчиняется закону двойного отрицания.

Закон двойного отрицания — это закон логики, позволяющий отбрасывать двойное отрицание. Его можно сформулировать так:

• • отрицание отрицания дает утверждение, или :
  • повторенное дважды отрицание ведет к утверждению.

Другими словами, чтобы получить истинное суждение, необходимо отрицать дважды: первый раз — в связке, второй раз — в предикате.

Например, исходное суждение:

«Все разумные люди хотят мира» (Все S есть Р).

В результате применения операции превращения преобразованным суждением станет суждение:

«Ни один разумный человек не хочет войны» (Ни одно S не есть не Р).

Превращать можно категорические суждения всех четырех видов:

1. А в Е:
   • Все освободительные войны являются справедливыми.
   • Ни одна освободительная война не является несправедливой.
2. Е в А:
   • Ничто на земле не проходит бесследно.
   • Все на земле оставляет след.
3. J в О:
   • Некоторые свидетели дают ложные показания.
   • Некоторые свидетели не дают правдивые показания.
4. О в J:
   • Некоторые приговоры суда не являются обвинительными.
   • Некоторые приговоры суда являются оправдательными.

В результате выполнения операции превращение:

1. 1. утвердительные суждения преобразуются в отрицательные, и наоборот;
   2. получается суждение, эквивалентное исходному.

На первый взгляд, представляется, что выполнение операции превращения не ведет к получению нового знания. Тем не менее происходит существенное уточнение исходной мысли .

Действительно, если в суждении большую информационную нагрузку несет предикат, то при выполнении операции превращения мы на тот же самый предмет мысли смотрим с противоположной точки зрения.

Обращение

В ходе операции обращения субъект и предикат суждения меняются местами (обращаются), при этом не меняется качество суждения.

Виды обращения (от распределенности терминов исходного суждения):

Если термины суждения оба распределены или оба не распределены, то обращение является чистым (простым). При таком обращении не меняется количественная характеристика суждения .

«Некоторые студенты проживают в общежитии».

Для преобразования данного суждения посредством операции обращения необходимо изобразить с помощью круговых диаграмм Эйлера отношение между субъектом «студенты» и предикатом «проживающие в общежитии». Эти понятия частично совпадают, оба термина не распределены, поэтому обращение будет чистым.

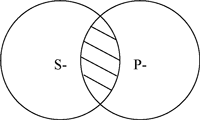
«Некоторые проживающие в общежитии студенты».

В случае, когда распределенность терминов суждения разная, обращение будет с ограничением, при котором поменяется количественная характеристика суждения .

«Граждане России имеют право на образование».

Отношение между понятием субъекта «граждане России» и понятием предиката «имеющие право на образование» является отношением подчинения, где предикат — подчиняющее понятие, а субъект — подчиненное.

Термин субъекта распределен, а предиката не распределен, поэтому обращение будет с ограничением и поменяется количественная характеристика суждения.

«Некоторые имеющие право на образование — граждане России».

Правила обращения различных типов суждений:

1. Суждения типа А в основном обращаются с ограничением. Исключением являются общеутвердительные суждения, в которых объемы понятий субъекта и предиката совпадают (выделяющие суждения и определения), поэтому оба термина являются распределенными, а обращение будет чистым.
2. Суждения типа J в основном преобразуются посредством чистого обращения, поскольку в этом типе суждений понятия субъекта и предиката частично совпадают. Исключением являются частноутвердительные выделяющие суждения, в которых объем предиката полностью входит в объем субъекта. Предикат распределен, а субъект не распределен. Преобразование этих суждений будет обращением с ограничением.
3. Суждения типа Е всегда обращаются без ограничения. Оба термина суждения всегда распределены, поскольку в таких суждениях весь объем субъекта исключается из всего объема предиката. Обращение будет чистым.
4. Суждения типа О не обращаются, к ним эта операция неприменима .

Точно так же, как и при выполнении операции превращения, в обращении необходимо увидеть, где оно — новое знание.

Если, как мы знаем, субъект — это то, о чем говорится в суждении, а предикат — то, что говорится о субъекте, и большую смысловую нагрузку несет именно предикат, то в результате выполнения операции обращения мы в новом суждении существенно уточняем наше представление об обоих терминах суждения.

Вспомните суждение «Мы не рабы». Какое суждение получится в результате обращения «Рабы не мы»? Если в первом суждении говорится о нас и о том, что никто из нас не является рабом, то во втором преобразованном суждении уже говорится о рабах и о том, что никто из рабов не является нами.

Преобразование по логическому квадрату

Данный вид непосредственного дедуктивного умозаключения опирается на основные логические законы, на которых основаны отношения между простыми категорическими суждениями.

Преобразованием по логическому квадрату называют непосредственное дедуктивное умозаключение, в результате которого из одного суждения можно вывести три, значения которых, в случае действия логических законов, будут известны.

Для иллюстрации отношений между простыми категорическими суждениями, подчиняющихся логическим законам, используется логический квадрат:

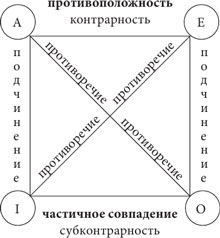
Отношение между суждениями типа А (общеутвердительное) и типа Е (общеотрицательное) называется отношением противоположности (контрарности) . Это отношение подчиняется логическому закону непротиворечия, согласно которому два противоположных суждения не могут быть одновременно истинными, по крайней мере, одно из них необходимо ложь.

Исходя из действия закона непротиворечия, если одно из противоположных суждений истинно, то второе — необходимо ложь:

• • если суждение А истинно, то суждение Е ложно;
  • если суждение Е истинно, то суждение А ложно.

Например, если суждение «Все люди смертны» (тип А) истинно, то противоположное ему суждение «Ни один человек не является смертным» (тип Е) необходимо ложно.

Точно так же, если суждение «Ни один человек не живет вечно» (тип Е) истинно, то противоположное ему «Все люди живут вечно» (тип А) ложно.

Но если первое суждение ложно, то второе является неопределенным по значению:

• • если суждение А ложно, то суждение Е либо истинно, либо ложно, то есть неопределенно;
  • если суждение Е ложно, то суждение А либо истинно, либо ложно, то есть неопределенно.

Например, если исходное суждение «Все студенты отличники» (тип А) ложно, то значение противоположного ему суждения «Ни один студент не является отличником» (тип Е) неопределенно.

Отношения между суждениями А (общеутвердительное) и О (частноотрицательное), а также Е (общеотрицательное) и J (частноутвердительное) называются отношением противоречия ( контрадикторности ). Это отношение подчиняется закону исключенного третьего, согласно которому два противоречащих суждения не могут быть одновременно ни истинными, ни ложными.

Исходя из действия закона исключенного третьего, если одно из противоречащих суждений истинно, то второе — необходимо ложь, и, наоборот, если первое суждение ложное, то второе — необходимо истинное.

Например, если суждение «Все люди смертны» (тип А) истинно, то противоречащее ему суждение «Некоторые люди не являются смертными» (тип О) необходимо ложно.

Точно так же, если суждение «Ни один человек не живет вечно» (тип Е) истинно, то противоречащее ему «Некоторые люди живут вечно» (тип J) ложно.

Если исходное суждение «Все студенты отличники» (тип А) ложно, то значение противоречащего ему суждения «Некоторые студенты не являются отличниками» (тип О) однозначно истинно.

Отношения между суждениями А (общеутвердительное) и J (частноутвердительное), а также Е (общеотрицательное) и О (частноотрицательное) называются отношением подчинения (контрарности) . Это отношение подчиняется закону достаточного основания, согласно которому истинности общего суждения достаточно для признания истинности частного суждения.

Исходя из действия закона достаточного основания, если общее суждение истинно, то и частное суждение будет необходимо истинным.

Например, из истинности суждения «Все люди смертны» (тип А) однозначно следует истинность частного суждения «Некоторые люди смертны» (тип J).

Но если общее суждение ложное, то значение частного суждения может быть как истинным, так и ложным, то есть является неопределенным: из ложного суждения «Все люди любят рыбий жир» (тип А) ничего нельзя сказать о значении ему подчиненного частного суждения.

Отношения между суждениями J (частноутвердительное) и О (частноотрицательное) называются отношением частичной совместимости (субконтрарности) . В этом виде отношения логические законы напрямую не действуют, поэтому из истинности первого частного суждения следует неопределенность второго суждения, следовательно, оно может быть как истинным, так и ложным.

В случае же, когда исходным является частное ложное суждение, значение второго частного суждения всегда будет истинным. В данном случае эта закономерность обусловлена последовательным действием двух логических законов: закона исключенного третьего и закона достаточного основания, согласно которым из ложности частного суждения следует истинность противоречащего ему общего суждения (закон исключенного третьего), а из истинности общего суждения следует истинность подчиненного ему частного суждения (закон достаточного основания).

Таким образом, преобразование по логическому квадрату позволяет судить о значении выводимых из исходного суждения суждений, значение которых может быть однозначным, если отношения между исходным и выводимым из него суждением подпадает под действие основных логических законов.

Знание зависимости истинности или ложности одних суждений от истинности или ложности других помогает делать правильные выводы в процессе рассуждения.

Противопоставление

Производными от превращения и обращения непосредственных умозаключений являются противопоставление субъекту или предикату.

Противопоставление — это логическая операция с простыми суждениями, производящая одновременно и обращение, и превращение суждений:

1) Если происходит сначала обращение , а потом превращение, то это противопоставление субъекту . Например:

«Все тигры — полосатые животные».

Применим к суждению операцию превращения:

Все тигры — полосатые животные. Ни один тигр не является не полосатым животным.

Теперь к полученному суждению применим операцию обращения:

Ни один тигр не является не полосатым животным . Ни одно не полосатое животное не является тигром.

2) В случае, когда происходит сначала превращение , а потом обращение, то это операция противопоставления предикату . Например:

«Некоторые студенты -иногородние».

Сначала применим к суждению операцию обращения:

Некоторые иногородние — студенты. Некоторые студенты — иногородние.

Теперь к полученному суждению применим операцию превращения:

Некоторые студенты — иногородние. Некоторые студенты не являются местными.

Источник

Непосредственные умозаключения

6.5.1 Понятие и специфика непосредственных умозаключений

Непосредственные умозаключения – это умозаключения, в которых вывод совершается из одной посылки, являющейся категорическим высказыванием.

К ним относятся превращение, обращение, противопоставление предикату, противопоставление субъекту и выводы по «логическому квадрату». Практически непосредственные умозаключения (кроме выводов по «логическому квадрату») представляют собой преобразования категорических суждений, в результате которых получаются суждения другой формы, но выражающие ту же самую мысль, что и исходные суждения.

Необходимость применять непосредственные умозаключения в человеческом общении основывается на том факте, что разные люди выражают свои мысли по-разному. Поэтому одну и ту же мысль трудно бывает узнать. Отсюда возникает проблема взаимопонимания, которая в логике сводится к выяснению того, в каких случаях разные по форме мысли имеют тождественное или сходное содержание.

Разрешить подобные вопросы в конкретных ситуациях иногда бывает довольно сложно. Действительно, возьмём два суждения:

а) Всякий трансцендентальный синтез является априорным.

б) Никакой неаприорный синтез не является трансцендентальным.

Далеко не каждый сможет сразу определить: выражают эти суждения одну и ту же мысль или нет. Но если подобные суждения встречаются, например, в споре, то реагировать нужно быстро, а для этого необходимо иметь навык работы с такого рода мыслями. Надо уметь узнавать одну и ту же мысль, высказанную в различных формах, и уметь доказывать, что то, что выдаётся за разное выражение одной и той же мысли, на самом деле таковым не является.

Непосредственные умозаключения как раз и позволяют выработать необходимый навык распознавания и отождествления разных по форме суждений с одним и тем же или близким смыслом.

6.5.2 Превращение

Превращение – это умозаключение, состоящее в преобразовании некоторого категорического суждения в противоположное по качеству с предикатом, противоречащим предикату исходного суждения.

Другими словами, при выводе с помощью превращения отрицательное суждение преобразуется в утвердительное и, наоборот, утвердительное – в отрицательное, а предикат берётся с отрицанием (то есть Р меняется на не-Р или не-Р на Р).

Формы выводов с помощью превращения:

1) для общеутвердительного суждения:

Ни одно S не есть не-Р.

2) для общеотрицательного суждения:

Ни одно S не есть Р.

3) для частноутвердительного суждения:

Некоторые S есть Р.

Некоторые S не есть не-Р.

4) для частноотрицательного суждения:

Некоторые S не есть Р.

Некоторые S есть не-Р.

Прежде чем преобразовать суждение при помощи операции превращения (а также при помощи других непосредственных умозаключений), его желательно записать в логической форме. Это позволяет не совершать ошибок при определении тех понятий, которые являются субъектом и предикатом категорических суждений, и таким образом избегать нелепостей при выводе. Причем, при записи категорического суждения в логической форме нужно помнить о том, что его субъект и предикат должны иметь общий род.

Пример. «Все жидкости упруги». Это общеутвердительное суждение (А). Записывая его в логической форме (Все S есть Р), получаем вывод:

Все вещества, являющиеся жидкостями (S),

есть вещества, являющиеся упругими (Р).

Ни одно вещество, являющееся жидкостью (S),

не есть вещество, не являющееся упругим (не-Р).

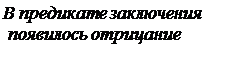Справедливы выводы и в обратную сторону – от нижнего суждения к верхнему.

6.5.3 Обращение

Обращение – это непосредственное умозаключение, состоящее в преобразовании категорического суждения в такое суждение, субъектом которого является предикат исходного, а предикатом – субъект исходного суждения.

Другими словами, при выводе с помощью обращения субъект и предикат меняются местами. При этом в случае, когда исходным суждением (посылкой) является общеутвердительное суждение, меняется также количество суждения, то есть заключение становится частным. Такое обращение называется «обращением с ограничением» или «чистым обращением».

Формы выводов с помощью обращения:

1) для общеутвердительного суждения:

Некоторые Р есть S.

2) для общеотрицательного суждения:

Ни одно S не есть Р.

Ни одно Р не есть S.

3) для частноутвердительного суждения:

Некоторые S есть Р.

Некоторые Р не есть S.

4) для частноотрицательного суждения путём обращения нельзя логически правильно вывести какое-либо заключение, так как в этом случае нарушается общее правило выводов из категорических суждений: термин, не распределённый в посылках, не должен быть распределён в заключении.

Пример 1. «Всякий студент обязан сдавать экзамены». Это общеутвердительное суждение, поэтому выполняем обращение с ограничением, записывая исходное суждение в логической форме (Все S есть Р):

Все люди, являющиеся студентами (S),

есть люди, обязанные сдавать экзамены (Р).

Некоторые люди, обязанные сдавать экзамены (Р),

есть люди, являющиеся студентами (S).

Обратите внимание на то,

что субъект посылки становится а предикат посылки —

предикатом заключения, субъектом заключения.

Пример 2. Если мы попытаемся сделать обращение из частноотрицательного суждения «Некоторые деревья не являются соснами», то заключение окажется явно некорректным:

Некоторые растения, являющиеся деревьями (S — ),

не есть растения, являющиеся соснами (Р + ).

Некоторые растения, являющиеся соснами (Р — ),

не есть растения, являющиеся деревьями (S + ).

Но мы знаем, что все сосны являются деревьями. Указав распределенность терминов, видим, что нарушается правило вывода из категорических суждений. В данном случае нераспределенный в посылке субъект (S — ), став предикатом в заключении, оказался распределен (S + ), а правило требует, чтобы термин, не распределенный в посылке, не был бы распределен и в заключении.

При выводах с помощью превращения и обращения необходимо учитывать существующие правила вывода: нельзя использовать посылки, содержащие пустые субъекты и предикаты (например, «существо, способное жить без пищи»), а также универсальные термины, то есть термины, выражающие универсальные понятия (например, «существо, нуждающееся в пище»).

Пример. В результате обращения суждения «Ни один человек (S) не может жить без пищи (Р)» получится заключение «Ни одно существо, которое может жить без пищи (Р), не есть существо, являющееся человеком (S)». Однако вывод полностью получается неправомерным, так как таких существ вообще нет. Дело в том, что в выводе использована посылка, в которой предикат («существо, которое может жить без пищи») представляет собой пустое понятие. Именно это и стало причиной неправомерности вывода.

6.5.4 Противопоставление предикату

Противопоставление предикату — это преобразование категорического суждения, в результате которого субъектом становится понятие, противоречащее предикату, а предикатом — субъект исходного суждения.

Такой вывод можно сделать, последовательно применяя превращение исходного суждения и далее обращение полученного при этом суждения либо следуя правилам для противопоставления предикату:

1) для общеутвердительного суждения:

Ни одно не-Р не есть S.

2) для общеотрицательного суждения:

Ни одно S не есть Р.

Некоторые не-Р есть S.

3) для частноотрицательного суждения:

Некоторые S не есть Р.

Некоторые не-Р есть S.

4) для частноутвердительных суждений нельзя проводить вывод путем противопоставления предикату, так как после превращения исходного суждения получается частноотрицательное суждение, для которого не применяется операция обращения.

Пример. Противопоставление предикату для частноотрицательного суждения «Некоторые озера не имеют стока»:

Некоторые водоемы, являющиеся озерами (S),

не есть водоемы, имеющие сток (Р).

Некоторые водоемы, не имеющие стока (не-Р),

есть водоемы, являющиеся озерами (S).

6.5.5 Противопоставление субъекту

Противопоставление субъекту—это преобразование категорического суждения, в результате которого субъектом становится предикат исходного суждения, а предикатом — понятие, противоречащее субъекту исходного суждения.

Такой вывод можно осуществить, последовательно применяя обращение исходного суждения, а затем — превращение полученного результата, либо сразу следуя правилам для противопоставления субъекту:

1) для общеутвердительного суждения:

Некоторые Р не есть не-S.

2) для общеотрицательного суждения:

Ни одно S не есть Р.

3) для частноутвердительного суждения:

Некоторые S есть Р.

Некоторые Р не есть не-S.

4) для частноотрицательных суждений не используются выводы с применением противопоставления субъекту, так как в процессе этого вывода мы должны были бы сделать обращение частноотрицательного суждения, для которого не применяется вывод посредством обращения.

Пример. «Ни один злой человек не может быть вполне справедливым». Это общеотрицательное суждение (Е). Приводя его к логической форме («Ни одно S не есть Р»), делаем вывод в соответствии с формой противопоставления субъекту для общеотрицательного суждения:

Ни один человек, являющийся злым (S),

не есть человек, который может быть вполне справедливым (Р).

Все люди, которые могут быть вполне справедливыми (Р),

есть люди, не являющиеся злыми (не-S).

6.5.6 Умозаключения по «логическому квадрату»

Умозаключения по «логическому квадрату» делаются из простых категорических суждений на основе отношений между ними, зафиксированных в «логическом квадрате».

Формы выводов по «логическому квадрату»:

1) отношение контрарности (противоположности) между общеутвердительным (А) и общеотрицательным (Е) суждениями характеризуется тем, что эти суждения не могут быть вместе истинными, следовательно:

А Е

2) отношение субконтрарности (частичной совместимости) между частноутвердительным (I) и частоотрицательным (О) суждениями характеризуется тем, что эти суждения не могут быть вместе ложными, то есть:

ùI ùO

3) отношение подчинениямежду общеутвердительным (А) и частноутвердительным (I) суждениями, а также между общеотрицательным (Е) и частноотрицательным (О) суждениями: истинность подчиняющего суждения обусловливает истинность подчиненного, а ложность подчиненного обусловливает ложность подчиняющего:

А Е ùО ùI

4) отношение контрадикторности между общеутвердительным (А) и частноотрицательным (О) суждениями, а также между общеотрицательным (Е) и частноутвердительным (I) суждениями характеризуется тем, что суждения не могут быть одновременно истинными и не могут быть одновременно ложными:

А Е ùА ùЕ О I ùO ùI

Пример. По «логическому квадрату» сделаем выводы из общеутвердительного суждения «Любой человек мечтает быть счастливым». Предположим, что оно истинно. Тогда мы можем сделать выводы на основе отношений контрарности, подчинения и контрадикторности.

1. Отношение контрарности:

А: Все существа, являющиеся людьми (S),

есть существа, мечтающие быть счастливыми (Р).

ùЕ: Неверно, что ни одно существо, являющееся человеком (S),

не есть существо, мечтающее быть счастливым (Р).

2. Отношение подчинения:

А: Все существа, являющиеся людьми (S),

есть существа, мечтающие быть счастливыми (Р).

I: Некоторые существа, являющиеся людьми (S),

есть существа, мечтающие быть счастливыми (Р).

3. Отношение контрадикторности:

А: Все существа, являющиеся людьми (S),

есть существа, мечтающие быть счастливыми (Р).

ùО: Неверно, что некоторые существа, являющиеся людьми (S),

не есть существа, мечтающие быть счастливыми (Р).

Предположим, что суждение ложно. Тогда мы можем сделать вывод на основе отношения контрадикторности:

ùА: Неверно, что все существа, являющиеся людьми (S),

есть существа, мечтающие быть счастливыми (Р).

О: Некоторые существа, являющиеся людьми (S),

не есть существа, мечтающие быть счастливыми (Р).

Источник