- Числа первой сотни
- Презентация «Методика изучения чисел в пределах сотни» презентация к уроку по математике (2 класс)
- Скачать:
- Предварительный просмотр:
- Подписи к слайдам:
- Лекция 2. Лекция Общие вопросы изучения натуральных чисел 5 Лекция Методика изучения чисел первого десятка 7
- Лекция 4. Изучение чисел первой тысячи
Числа первой сотни
Десять десятков — это сотня. Числа от 11 до 100 называют числами первой сотни. Все числа первой сотни — двузначные.
Двузначные числа записывают двумя цифрами: 37, 45, 64, 40. Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа — цифрой второго разряда или разряда десятков.
Целые десятки (10 20 30 40 50 60 70 80 90) иногда именуются разрядными числами.
Читают двузначные числа слева направо. Для чисел 21 — 100 порядок называния составляющих их разрядных чисел и порядок записи совпадает: 21 (двадцать один)
Понятие «разряд» является базовым для образования чисел первой сотни.
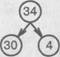
Разрядный состав — выделение разрядных чисел в двузначном числе:
На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания:
30-+ 4 34-4 34 — 30
При нахождении значений этих выражений ссылаются на разрядный состав двузначных чисел: число 34 состоит из 30 и 4. Вычитая 30 получаем 4.
Разрядные слагаемые — сумма разрядных чисел двузначного числа:
47 = 40 + 7 68 — 60 + 8
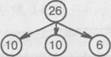
Десятичный состав — выделение десятков и единиц в двузначном числе:
26 — это 2 дес. и 6 ед.
Схема десятичного состава:
На основе схемы десятичного состава можно рассмотреть такие случаи сложения и вычитания:
26-6 26-20 26-10 26-16 20 + 6
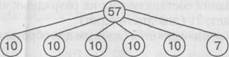
При нахождении значения этих выражений ссылаются на десятичный состав (десятичную схему) двузначного числа: вычитая из числа 26 число 16 (1 десяток и 6 единиц) получаем 1 десяток. Для наглядности ребенок прикрывает вычитаемое рукой на схеме. В дальнейшем это действие ребенок выполняет мысленно и сразу называет и пишет ответ. Использование десятичной схемы двузначного числа значительно облегчает вычислительную деятельность детям, которым вычисления «в уме» даются трудно. Например, десятичная схема числа 57 дает возможность без применения каких-либо еще вспомогательных приемов вычислений решить следующие примеры:
57 — 10 57 — 20 57 — 30
57 — 40 57-50 50 + 7
57 — 17 57 — 27 57 — 37
а также легко справиться со случаями вида: 57 + 2; 57 + 3; 57 + 10 и т. п., используя прием «десятки к десяткам, а единицы к единицам».
При изучении нумерации двузначных чисел рассматривают также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел: 43 + 1; 43 — 1; 40 + 1; 40-1.
При нахождении значения этих выражений, ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.
Приведем основные виды заданий, выполняемых детьми при изучении чисел первой сотни:
1) на способ образования чисел первой сотни:
Назови число, в котором 1 дес. 9 ед., 2 дес. 7 ед., 9 дес. 2 ед. 62
Запиши числа, в которых 3 дес. 1 ед., 7 дес. 3 ед., 7 дес. О ед.
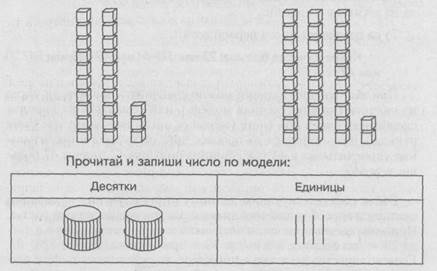
2) на соотнесение количественной модели, названия и записи числа:
Сколько кубиков на каждом рисунке?
3) на принцип образования натурального ряда чисел:
Уменьши на 1: 20, 47, 32, 50, 70
Увеличь на 1: 19, 28, 44, 67, 40, 90
Найди значение выражения: 50 + 1; 44 + 1; 68 — 1; 90 — 1.
Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.
4) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи числа: 72, 20, 70, 27? (В записи числа 72 цифра 7 обозначает количество десятков, а цифра 2 — количество единиц,. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)
5) на место числа в ряду чисел:
Вставь пропущенные числа: 40, 41 . 43. 47. 50
Вставь пропущенные числа: 70, 69. 64. 61 .
При выполнении задания ссылаются на порядок чисел при счете.
6) на разрядный состав:
20 + 3 = 23 23-3 = . 23-20 = .
37 = 30 + 7 37-30 = . 37-7 = .
При выполнении задания ссылаются на разрядную модель числа из десятков и единиц.
7) на сравнение чисел первой сотни:
Какое из чисел больше: 23 или 32? 44 или 47? 28 или 54? 20 или 4?
При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 44 три единицы получим 47, значит 47 больше, чем 44).
Более соответствующим данному этапу изучения нумерации считается способ сравнения чисел с опорой на разрядный состав. При этом сравнивать числа начинают со старших разрядов: в числе 23 — два десятка, а в числе 32 — три десятка, значит 32 > 23. Если количество десятков одинаковое, то сравнивают цифры разряда единиц: в числе 44 и числе 47 по 4 десятка, сравним разряд единиц — 7 больше, чем 4, значит 47 > 44.
Сравнивая двузначные числа с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные.
Источник
Презентация «Методика изучения чисел в пределах сотни»
презентация к уроку по математике (2 класс)
Презентация содержит пошаговую методику изучения чисел в пределах сотни с наглядным материалом и поэтапностью хода урока. Пригодится в использовании учителям начальной школы, студентам педагогических вузов
Скачать:
| Вложение | Размер |
|---|---|
| matem._dlya_publikatsii.pptx | 1.69 МБ |
Предварительный просмотр:
Подписи к слайдам:
Методика преподавания математики в специальной школе V вида Тема: Методика изучения чисел в пределах сотни Подготовила: Медникова К.О.
Десять десятков – это сотня. Числа от 11 до 100 называют числами первой сотни. Все числа первой сотни двузначные .
Двузначные числа записывают двумя цифрами: 12, 24, 37, 40, 58, 64, 73, 81, 99. Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа – цифрой второго разряда или разряда десятков.
Целые десятки (10 20 30 40 50 60 70 80 90) иногда именуются разрядными числами. Читают двузначные числа слева направо.
Для чисел 21 – 100 порядок называния составляющих их разрядных чисел и порядок записи совпадает: 21 (два- дцать один) Понятие «разряд» является базовым для образования чисел первой сотни.
Разрядный состав – выделение разрядных чисел в двузначном числе: 34 30 4
На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания: 30 + 4 34 — 4 34 — 30 При нахождении значений этих выражений ссылаются на разрядный состав двузначных чисел: число 34 состоит из 30 и 4. Вычитая 30 получаем 4.
Разрядные слагаемые – сумма разрядных чисел двузначного числа: 47 = 40 + 7 68 = 60 + 8 Десятичный состав – выделение десятков и единиц в двузначном числе: 26 – это 2 дес . и 6 ед.
Схема десятичного состава: На основе схемы десятичного состава можно рассмотреть такие случаи сложения и вычитания: 20 – 6 26 – 20 26 – 10 26 – 16 20 + 6 26 10 10 6
При нахождении значения этих выражений ссылаются на десятичный состав (десятичную схему) двузначного числа: вычитая из числа 26 число 16 (1 дес . и 6 ед.) получаем 1 десяток. Для наглядности обучающийся прикрывает вычитаемое рукой на схеме. В дальнейшем это действие обучающийся выполняет мысленно и сразу называет и пишет ответ. Использование десятичной схемы двузначного числа значительно облегчает вычислительную деятельность детям, которым вычисления «в уме» даются трудно.
Например, десятичная схема числа 57 дает возможность без применения каких-либо еще вспомогательных приемов вычислений решить следующие примеры: 57 – 10 57 – 20 57 — 30 57 – 40 57 – 50 50 + 7 57 – 17 57 – 27 57 – 37 А также легко справиться со случаями вида: 57 + 2; 57 + 3; 57 + 10 и т.п., используя прием «десятки к десяткам, а единицы к единицам». 57 10 7
При изучении нумерации двузначных чисел рассматривают также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел: 43 +1; 43 – 1; 40 + 1; 40 – 1. При нахождении значения этих выражений, ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.
Приведем основные виды заданий, выполняемых детьми при изучении чисел первой сотни: 1) На способ образования чисел первой сотни: Назови число, в котором: 1 дес . 9 ед., 2 дес . 7 ед., 9 дес . 2 ед. Запиши числа, в которых: 3 дес . 7 ед., 7 дес . 3 ед., 7 дес . 0 ед.
2) На соотнесение количественной модели, названия и записи числа: Сколько кубиков на каждом рисунке?
3) На принцип образования натурального ряда чисел: Уменьши на 1: 20, 47, 32, 50, 70 Увеличь на 1: 19, 28, 44, 67, 40, 90 Найди значение выражения: 50 + 1; 68 – 1. Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.
4) На поместное значение цифры в записи числа: Что обозначает каждая цифра в записи числа: 72, 20, 70, 27? (В записи числа 72 цифра 7 обозначает количество десятков, а цифра 2 – количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)
5) На место числа в ряду чисел: 5) На место числа в ряду чисел: Вставь пропущенные числа: 40, 41 … 43 … … … 47 … … 50 Вставь пропущенные числа: 70, 69 … … … … 64 … … 61 … При выполнении задания ссылаются на порядок чисел при счете.
6) На разрядный состав: 20 + 3 = 23 23 – 3 = 23 – 20 = 37 = 30 + 7 37 – 30 = 37 – 7 = При выполнении задания ссылаются на разрядную модель числа из десятков и единиц.
7) На сравнение чисел первой сотни: Какое из чисел больше: 23 или 32? 44 или 47? 28 или 54? 20 или 4? При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания или отсчитывания (присчитывая к 44 три единицы получим 47, значит 47 больше, чем 44).
Более соответствующим данному этапу изучения нумерации считается способ сравнения чисел с опорой на разрядный состав. При этом сравнивать числа начинают со старших разрядов: в числе 23 – два десятка, а в числе 32 – три десятка, значит 32 > 23. Если количество десятков одинаковое, то сравнивают цифры разряда единиц: в числе 44 и числе 47 по 4 десятка, сравним разряд единиц – 7 больше, чем 4, значит 47 > 44. Сравнивая двузначные числа с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные.
При сравнении чисел вида: 99 … 100 67 … 68 98 … 99 59 … 60 100 … 100 20 … 21 следует ссылаться на порядок следования чисел при счете: следующее число всегда больше, чем предыдущее. Для наглядного сравнения чисел первой сотни можно использовать портновскую ленту. >Мне нравится
Источник
Лекция 2. Лекция Общие вопросы изучения натуральных чисел 5 Лекция Методика изучения чисел первого десятка 7
| Название | Лекция Общие вопросы изучения натуральных чисел 5 Лекция Методика изучения чисел первого десятка 7 |
| Дата | 27.01.2020 |
| Размер | 380.79 Kb. |
| Формат файла |  |
| Имя файла | Лекция 2.docx |
| Тип | Лекция #105943 |
| страница | 5 из 6 |
 С этим файлом связано 1 файл(ов). Среди них: Сетевые педагогические сообщества.docx. Показать все связанные файлы Подборка по базе: Дискуссионные вопросы.docx, БД Тестовые вопросы по ХД.docx, Тема 1 общие вопросы ППС.doc, криминология вопросы.doc, Налоги и налоговая система все вопросы.pdf, Экзаменационные вопросы и тесты (факультетская хирургия).doc, Контрольные вопросы.rtf, 03.11.2021 Деловые игры в экономике, Лекция.docx, Материаловедение. Лекция 2.doc, Ответы на вопросы по уголовно-исполнительному праву.doc Лекция 4. Изучение чисел первой тысячи1. Задачи изучения темы. 2. Методика изучения чисел первой тысячи: 2.1 Формирование понятия сотни. 2.2 Изучение устной нумерации. 2.3 Изучение письменной нумерации. 2.4Виды заданий при изучении чисел первой тысячи. 3. Средства изучения чисел первой тысячи. 1. Познакомить учащихся с новой счетной единицей – сотней и с разрядом сотен. 2. Закрепить понимание позиционного построения десятичной системы счисления. 3. Разъяснить соотношение разрядных единиц в трехзначном числе. (10ед = 1дес, 10дес = 1сот.) 4. Научить определять количество десятков и сотен в трехзначном числе (десятичный состав числа). 5. Сформировать умение читать и записывать трехзначные числа. 6. Сформировать умение складывать и вычитать числа на основе разрядного состава трехзначных чисел. 7. В связи с изучением нумерации трехзначных чисел рассмотреть соотношения единиц длины (дм, м, км.) 2.1Формирование понятия сотни Изучение устной нумерации в пределах тысячи начинается с формирования у учащихся понятия о сотне как о новой счетной единице. Для этого считают предметы по одному, десятками, сотнями (сто, двести,,…..девятьсот, тысяча). В практике часто используют палочки в пучках, также можно использовать пособие «Квадраты и полоски». 2.2 Изучение устной нумерации. — Чтобы у учащихся не сложилось неправильное представление о натуральной последовательности чисел за пределами первой сотни, следует включать упражнения в счете предметов или присчитывании по одному. Для этого можно использовать ленту «тысячи» или рулетку. — На следующем этапе учащиеся знакомятся с образованием чисел из сотен, десятков и единиц. Используя наглядные пособия, учащиеся получают и изображают числа и учатся называть эти числа. Выполняются и упражнения обратного характера – указать, сколько сотен, десятков и единиц содержится в названном числе. — При изучении устной нумерации дети учатся устанавливать общее число разрядных единиц в числе (десятичный состав числа). Опираясь на наглядные пособия, учитель показывает, что , например, в числе 345 имеется 4 десятка, но если сосчитать все десятки, т.е. и те которые сгруппированы в сотни, то в данном числе содержится 34 десятка. Аналогично выясняем количество единиц в этом числе. – Одновременно с разъяснением десятичного состава числа ведется работа над натуральной последовательностью. С этой целью включают упражнения, выполняемые сначала с опорой на наглядность, например: «Покажите часть ленты длиной290см; присчитывайте (отсчитывайте) по 1см (по 10см, по 100см). Найдите на ленте «тысячи» числа 400,399. Какое из них больше? На сколько? Назовите число следующее за числом 799, предшествующее числу 1000? 2.3 Изучение письменной нумерации. — При ознакомлении с письменной нумерацией чисел в пределах 1000, опираясь на умения детей записывать двузначные числа, надо показать, что сотни, т.е. единицы III разряда, записываются на третьем месте справа. Вначале учащиеся иллюстрируют числа с помощью предметов и обозначают их цифрами, например: 65, 165, 365, 360, 305. Целесообразно при этом располагать палочки или квадраты в таблице (абаке) под соответствующими названиями разрядов. Далее учащиеся записывают числа в таблицу разрядов. Для усвоения способа чтения и записи трехзначных чисел: — образуют числа, читают числа по модели; — соотносят вещественную модель и символическую запись; — используют схематические разрядные модели. Особое внимание следует уделять числам, в записи которых имеются нули. 2.4 Виды заданий, выполняемых при изучении чисел первой тысячи. 1) На способ образования чисел первой тысячи: — Назови число, в котором 3сот. 1дес. 9ед.; 1сот.2дс.7ед. — Запиши числа, в которых 3сот. 0дес. 7ед.; 1сот.7дес.3ед. — Сколько всего палочек, если есть: 2 пучка по 100 палочек,4 пучка по 10 палочек и 5 палочек? 2) На соотнесение количественной модели, названия и записи числа: — Как с помощью палочек изобразить в таблице числа: двести тридцать шесть? Триста пять? — Прочитай числа, записанные в таблице:
-Запиши в таблице и прочитай числа: 7сот.3дес. 3ед.; 4сот. 6дес. 0ед.
3) На принцип образования натурального ряда: — Какое число при счете следует за числом 199, 999. Какое число предшествует числу 840? 1000? — Увеличь на 1: 199,287, 444, 67, 901. — Найди значение выражения: 500-1; 744+1; 689+1; 990-1. — Что обозначает каждая цифра в записи чисел: 894, 809, 408, 900? — Сколько всего цифр использовано для записи каждого числа: 578, 785? Используя эти же цифры, запиши другие трехзначные числа. — Во Дворце спорта в одном ряду были свободны места с 231 по 240. Назови, какие места свободны. — Замени число суммой по образцу: 195=100+90+5, -Заполни пропуски, чтобы равенства были верными: 999 = ….+90+9; 564=500+….+4. — Вычисли: 400+80-1, 978-8-1, 500+99+1, 750-50+1. — Какое из чисел больше: 709 или 789, 578 или 571, 499 или 500, 300 или 150? — Расположи числа в порядке убывания: 658, 397, 542, 488, 165. — Сколько десятков в числах: 150, 270, 400? — Запиши 5 чисел, в которых содержится 37 десятков. Сколько всего таких чисел? — Сколько единиц составляют 5сот., 2сот., 24дес.? — В прыжке с шестом спортсмен взял высоту 600см. Вырази эту высоту в метрах. — Заполни пропуски, чтобы равенства были верными: 1сот. =10дес. ….ед., 10сот =100дес. =……ед. 1. Пучки палочек. 2. Лента «тысячи». Лента шириной 3-5см и длиной 10м изготавливается из плотной бумаги, на ней различным цветом обозначены метры (сотни),дециметры (десятки), сантиметры (единицы). Источник |
