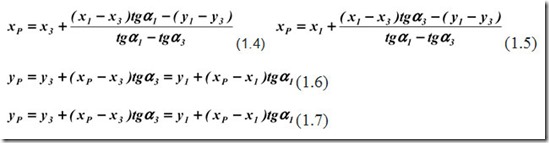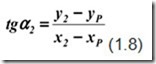Обратная угловая засечка в геодезии
Доброго времени суток, уважаемые читатели моего блога!
Определение положения точки посредством измерения углов (направлений) на определяемой точке, на три и более пункта с известными координатами в геодезии – это и есть обратная угловая засечка. Если исходных пунктов три – это однократная угловая засечка, если больше – многократная угловая засечка.
Французский математик Л.Потенот в 1692 году предложил математическое решение задачи по определению координат искомой точки по известным координатам трёх других точек. Сейчас решений этой задачи существует более ста. Один из видов решения – использование формул Жана Деламбра, французского геодезиста, астронома, метролога. Обратная засечка по Деламбру определяется через нумерацию исходных точек и углов по часовой стрелке с выбранным начальным направлением.
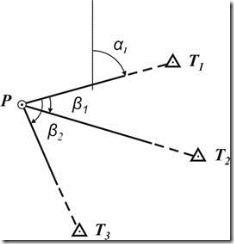
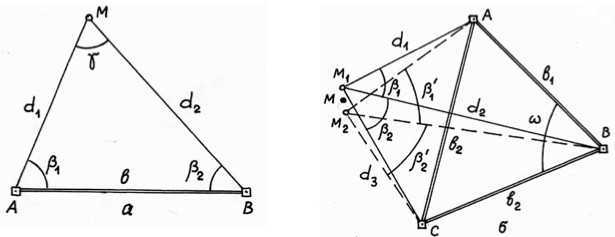
На рисунке 1 начерчена схема обратной засечки в соответствии с формулами Деламбра. Пункты триангуляции Т1, Т2, Т3 – исходные, точка (пункт) Р – определяемая, выбрано начальное направление – РТ1, на пункте Р измерены углы β1, β2 в направлении пунктов Т2, Т3.
Рис. 1. Обратная однократная угловая засечка (схема).
Сначала нужно определить дирекционный угол начального направления РТ1:
Итог: прямая угловая засечка с известными углами направлений с точки Р на исходные пункты. Известный способ определения координат Хр, Ур точки Р – это необходимое и достаточное применение формул Гаусса, которые выражаются через координаты исходных точек, вернее, их приращения:
Вычисления координат пункта Р происходит дважды; процесс вычисления, таким образом контролируется. Угол α2 высчитывается так:
Необходимо понимать, что значения α2, которое произведено по формуле 1.8, может не соответствовать значению, вычисленному по формуле 1.2 – на 180 градусов. Это связано с тем, что знаки числителя, знаменателя (формула 5.1) не могут определить приращения координат ∆х, ∆у. Контролируемое значение α2 требует определения знаков и четверти на карте проекта, где отмечены вставки точек методом обратной засечки.
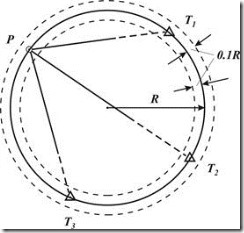
Аксиомой является то, что у обратной угловой засечки с тремя исходными пунктами нет решения, если пункт, который определяется, расположен на одной и той же окружности, что и исходные точки. Такая окружность называется «опасной». Удаление от неё определяемой точки на 0,1 х R (радиус окружности), обеспечит точность местоположения пункта, который является искомым.
Рис. 2. «Опасная» зона в обратной угловой засечке.
Если при схематичном составлении на карте (плане) обратной угловой засечки, пункт, который вычисляется, расположен в границах треугольника с вершинами – исходными пунктами (точками), можно констатировать, что «опасной окружности» здесь нет. В иных случаях, сообразно геометрическим законам, на карте (плане) строится окружность, которая проходит через 3 исходных пункта, после чего визуально определяется «опасная» зона для вычисляемого пункта.
Для работы по формулам обратной угловой засечки существует программа вычислений в режиме он-лайн, которая базируется на сайте map-info.ru. Ещё один способ определения необходимого пункта – это обратная линейно – угловая засечка. О ней поговорим в следующий раз.
На этом все друзья. Спасибо за внимание. Отличного Вам дня и хорошего настроения. Пока!!
Источник
Способы прямой и обратной угловых засечек
Способ угловой засечки применяют для разбивки недоступных
точек, находящихся на значительном расстоянии от исходных
пунктов.
Различают прямую и обратную угловые засечки.
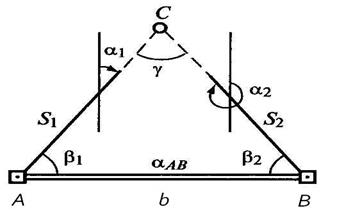
В способе прямой угловой засечки положение на местности проектной точки С (рис. 1) находят отложением на исходных пунктах А и В проектных углов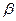 
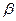
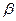
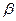
1 и 2. Базисом засечки служит или специально измеренная сторона, или сторона разбивочной сети. Проектные углы 1 и 2 вычисляют как разность дирекционных углов сторон. Дирекционные углы находят из решения обратной геодезической задачи по проектным координатам определяемой точки и известным координатам исходных пунктов.
Рисунок 1 − Схема разбивки способами прямой и линейной засечек
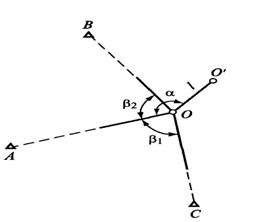
Способ обратной угловой засечки. На местности находят приближенно
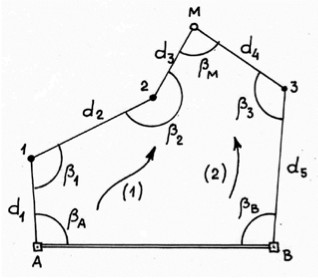
положение О’ разбиваемой точки О (рис. 2). В этой точке устанавливают теодолит и с требуемой точностью измеряют углы не менее чем на три
исходных пункта с известными координатами. По формулам обратной засечки вычисляют координаты приближенно определенной точки и сравнивают их с проектными значениями. По разности координат вычисляют величины редукции (угловой и линейный элементы) и смещают точку в проектное положение.
Для контроля на этой точке измеряют углы, вновь вычисляют ее координаты и сравнивают их с проектными. В случае недопустимых расхождений все действия повторяют.
Рисунок 2 − Схема способа обратной угловой засечки
Источник
Способы разбивочных работ
Способ прямой и обратной угловых засечек. Чаще всего эти способы применяют для выноса недоступных точек, а также точек, находящихся на значительных расстояниях от геодезической основы.
В способе прямой угловой засечки (см. рис. а) положение точки М определяют с исходных пунктов А и В геодезической основы построением в каждой из них горизонтальных углов β1 и β2, которые являются разбивочными элементами. Указанные углы строят на местности по правилам, изложенным в § 88. В данной схеме целесообразно использовать одновременно два теодолита. При этом положение проектной точки фиксируют по команде двух наблюдателей при положениях КЛ, а затем – при положениях КП. После фиксирования среднего положения точки М выполняют контрольное измерений углов β1 и β2.
Необходимо иметь в виду, что величина угла γ при точке М не должна быть малой и слишком большой. Оптимальным углом, при котором вынос точки может быть выполнен с меньшей погрешностью, является γ ≈109 0 − 110 0 при примерно равных расстояниях от исходных точек до точки М. То есть следует стремиться обеспечить симметричную схему построения точки М. Кроме того, для повышения точности построения проектной точки, а также для контроля её построения, вынос проектной точки на местность выполняют часто с двух базисов геодезической разбивочной основы.
Во многих случаях бывает сложно из одного приема вынести точку М с заданной точностью в её проектное положение. В таких случаях используют способ замкнутого треугольника. Вынос точки осуществляют последовательными приближениями. Для этого с максимально возможной точностью выполняют построение точки М, затем несколькими приёмами измеряют все углы треугольника, уравнивают углы и вычисляют координаты точки М из решения по формулам прямой угловой засечки. Полученные координаты сравнивают с проектными и при недопустимых отклонениях в их значениях определяют поправки (редукции) в положение точки М и смещают последнюю в проектное положение. Для контроля снова измеряют углы и выполняют аналогичные вычисления.
Вынос проектной точки способами прямой и обратной угловых засечек: а) способ прямой угловой засечки; б) способ обратной угловой засечки
Вынос на местность проектной точки способом полярных координат
Вынос на местность проектной точки способом проектного полигона
Метод последовательных приближений используют и в способе обратной угловой засечки (см. рис. б). Предварительно точку М выносят на местность и измеряют при ней углы β1 и β2. По формулам обратной угловой засечки определяют координаты точки М и сравнивают их с проектными. При необходимости положение точки М редуцируют на величины отклонений по координатам Х и Y, точку М фиксируют в положении М2 и снова уже в новой точке измеряют горизонтальные углы β а затем вычисляют координаты новой точки М. Все указанные действия выполняют до тех пор, пока задача качественного построения проектной точки не будет решена.
Способ полярных координат используют в тех случаях, когда проектные точки находятся сравнительно недалеко от точек геодезической основы. При этом предпочтительно, чтобы расстояния до них не превышали длины мерного прибора (ленты или рулетки).
На местности от исходного направления АВ (см. рис.) строят проектный угол β и проектное расстояние d, которые в данном способе являются разбивочными элементами.
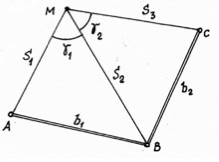
Проектная точка может находиться далеко от точек геодезической основы или не может быть вынесена по техническим условиям способами угловой засечки. В таких случаях к точке прокладывают полигонометрический ход (см. рис.), используя для этого последовательно расчётные проектные углы и проектные расстояния. Данный способ называют способом проектного полигона.
По двум ходам от базисной линии АВ геодезической основы получают два положения точки М из решения ходов (1) и (2). В качестве первого приближения вычисляют средние значения координат проектной точки. Затем в полученной точке М измеряют угол βМ и линии d3 и d4 и вычисляют координаты точки М в общей схеме замкнутого полигона. Если координаты точки М будут значительно отличаться от проектных, то определяют поправки (редукции) в положение точки М, точку смещают и снова измеряют угол βМ и линии d3 и d4. Из решения хода находят координаты точки М и сравнивают их с проектными. Такие действия выполняют до достижения необходимой точности построения проектной точки.
Вынос на местность проектной точки способом линейной засечки
Способы створных засечек: а) способ створно-линейной засечки; б) способ створной засечки
При небольших расстояниях от проектной точки до точек геодезической основы удобно использовать способ линейной засечки, реализуемый с помощью двух или трёх рулеток (см. рис.). Разбивочными элементами в этом способе являются только расстояния S или горизонтальные проложения.
Для выноса осей сооружений удобно использовать способы створных засечек (см. рис.).
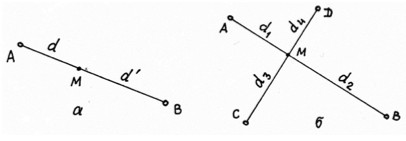
В схеме створно-линейной засечки (см. рис. а) положение точки М определяют на линии створа, образованного пунктами А и В геодезической основы. По линии створа проектным расстоянием d задают положение искомой точки М. При необходимости положение точки М может быть проконтролировано с другой точки створа. В точке А створа устанавливают теодолит, а в точке В – визирную цель (на штативе, с возможностью центрирования и горизонтирования).
В схеме створной засечки (см. рис. б) точку М задают на линии пересечения створов АВ и СD. Для повышения точности работу целесообразно выполнять одновременно двумя теодолитами и двумя визирными целями несколькими приёмами с перестановкой теодолитов и визирных целей. Для контроля измеряют расстояния от построенной точки до исходных пунктов геодезической основы.
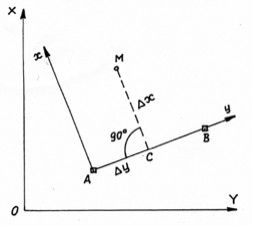
Обычно на строительной площадке имеется т.н. строительная сетка. В её системе координат задано положение всех осей (главных, основных и т.д.), а также всех главных (узловых) точек. В этом случае вынос проектных точек осуществляется в системе координат строительной сетки по приращениям координат Δx и Δy (см. рис.). В общегосударственной или местной системах координат ХОY используется система координат хАy строительной сетки c началом координат в точке А. Ось Аy задается исходным направлением на другую исходную точку (В) геодезической основы. Положение точки М определяется расстояниями Δx и Δy, т.е. приращениями координат в системе координат строительной сетки.
Разбивка точек сооружения от строительной сетки
Способ бокового нивелирования
Предварительно строят проектное расстояние Δy, устанавливают в полученной точке С теодолит, строят проектный угол β, равный 90 0 на точку М и в полученном направлении откладывают отрезок Δx. Для обеспечения более высокой точности построения точки меньшее из Δx и Δy следует строить в виде перпендикуляра, а большее – по створу исходной линии.
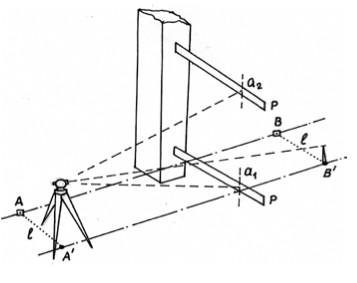
Вынос вертикальных осей конструкций выполняют способом бокового нивелирования (см. рис.). От оси АВ, на которой находится строительная конструкция, например, колонна, а небольшом расстоянии l строят линию А’В’, параллельную исходной линии АВ. В точке А’ устанавливают теодолит, который визируют на марку, находящуюся в точке В’. Перпендикулярно к оси колоны последовательно на её основание и верх устанавливают рейку Р (с уровнем, ориентированным осью по продольной оси рейки) и берут отсчёты а1 и а2 по вертикальной нити сетки зрительной трубы. Равенство указанных отсчётов определяет вертикальность оси колонны. Если расхождение между отсчётами недопустимо, то положение вертикальной оси колонны выправляют.
Оставьте свой отзыв, комментарий или задайте вопрос
Источник
