Способ обратной засечки тахеометром

Обратная засечка тахеометром по двум точкам

Привет друзья и коллеги!

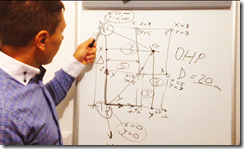
Если вы пользовались тахеометром, то знаете, что он работает в системе условных координат. И для того что бы привязаться к точкам нужно знать их координаты, так как прибор их запрашивает. Но что делать когда вы не знаете координаты точек. В этом случае вы можете одну из них принять за начало координат, с координатами Х=0 и У=0.

А координаты второй точки можно высчитать, зная расстояние между ними. Вот и получается все что нам нужно знать – это расстояние между точками. Определить расстояние можно рулеткой, а еще лучше с помощью тахеометра. Для этих целей в тахеометре Sokkia есть специальная функция ОНР – определение недоступного расстояния.

Следующий этап – нужно задать направление осям координатной сетки нашей условной системы координат. Лучше всего направить оси так, что бы точки объекта с которым будем работать, имели положительные значения координат по оси Х и по оси У.

Задав направление осям координат и зная расстояние между точками мы без труда вычислим координаты этих точек. А уже зная координаты мы сможет с помощью обратной засечки привязаться к ним. После привязки тахеометр будет настроен и будет работать в условной системе координат, которую мы сами создали. Фактически прибор определяет координаты точки стояния прибора. Точка стояния прибора или станция это точка в которой пересекаются вертикальная ось вращения тахеометра и ось вращения трубы. А зная свои координаты, тахеометр может вычислить координаты любой точки на которую мы сделаем измерения.

Следующий этап – это вычисление координат точек, которые нужно вынести в натуру. Зная расстояния от этих двух точек до точек, которые будем выносить, мы без труда высчитаем их координаты.

И последний этап, засекаемся от наших двух точек обратной засечкой и выносим в натуру наше строение. Весь это процесс я для наглядности записал на видео.

Обязательно поставьте лайк, если видео вам понравилось и принесло пользу. На этом все друзья, встретимся в следующем выпуске.

Источник

Обратная угловая засечка в геодезических измерениях

Засечкой называют относительно простой метод вычисления координат некоторой точки посредством измерения на ней углов и расстояний по направлению на уже закрепленные на местности контуры.

К ней достаточно часто прибегают в различных геологических, строительных и инженерных работах за счет ее простоты и экономичности. На практике обратная засечка чаще всего используются для вычисления координат пунктов геодезической сети, выноса в натуру проектных точек и т.д.

Опытный геодезист сможет без труда провести нужные измерения при помощи теодолита, тахеометра или любого другого прибора всего за пару минут.

Виды засечек

В зависимости от местности и способов построения сетей сгущения в геодезии существует два основных вида привязки к опорным пунктам:

1. Непосредственная. Подразумевает привязку теодолитного или полигонометрического хода к триангуляционным пунктам высшего класса с возможностью выполнить измерения примычных углов. Используется в тех случаях, когда на опорных точках можно выполнить те же измерения, что и на соседних.
2. Косвенная. Проводится только при отсутствии возможности провести непосредственные измерения примычных длин и углов. К этому виду привязки и относится засечка.

По способу же построения геодезическая засечка бывает:

• линейной (полярные и биполярные по числу пунктов);
• угловой (прямая и обратная);
• комбинированной (положение точки определяют по известным углам и линейным расстояниям).

В геодезии чаще всего прибегают к комбинированию прямой и обратной засечек. Кроме того, чтобы полученные результаты были наиболее достоверными, измеряют больше величин, чем нужно, а само местоположение искомых пунктов получают посредством уравнивания.

Однократная и многократная засечка

Если для определения координат берется только один исходный пункт, то такая засечка будет называться однократной, а если более трех – многократной.

В основе обратной однократной угловой засечки лежит так называемая задача Потенота, которая была названа в честь французского математика Лорана Потенота, удачно решившего ее еще в 1692 году. Ученый предложил по известным значениям трех близлежащих точек вычислять координаты искомой.

На сегодняшний день существует уже более ста вариаций ее решения, которые были предложены многими именитыми учеными, но в геодезической практике наибольшую популярность получили формулы Жана Деламбра, Кнейссля и Гаусса.

Рисунок 1. Обратная многократная засечка

Важно отметить, что достоверные данные удается получить только в тех случаях, когда искомая точка находится в пределах треугольника, который образовали исходные пункты или же вне его, но напротив одной из его вершин.

Если же искомая точка попадает в пределы окружности, проходящей через эти точки, она становится неопределяемой. Этот ключевой недостаток в задаче Потенота, именуемый опасным кругом, приводит к необходимости определения дополнительной точки.

Обратная многократная угловая засечка как раз и подразумевает определение местоположения пункта через измерения на этом самом пункте углов или направлений как минимум на четыре твердых пункта, чьи координаты установлены. Этот метод более трудоемкий, но гарантирует надежный контроль результатов измерений. При обработке данных используют метод Гаусса-Ньютона, который в геодезии также называют параметрическим.

Способ Деламбра

Решение обратной засечки при помощи этого способа выполняется в такой последовательности:

Вычисляется дирекционный угол исходного направления с отметки 1 на точку «0» по формуле обратной геодезической засечки:

Значения дирекционных углов с исходных отметок Т2, Т3, Т4 получают из формул:

Находят координаты точки Р с помощью формул тангенсов или котангенсов дирекционных углов направлений.

Способ Кнейссля

Аналогично способу Деламбра последовательность формул при решении задачи обратной геодезической засечки по Кнейсслю будет иметь следующий вид:

Определяются вспомогательные коэффициенты:

Вычисляется котангенс дирекционного угла исходного направления на заданный пункт:

Приращения координаты точки Р относительно исходного пункта 1 находят при помощи нижеприведенных формул:

\(\Delta x_<1-p>=c\cdot \Delta y_<1-p>\)

Определяются координаты точки Р:

\(y_

=y_<1>+\Delta y_<1-p>\)

Средняя квадратическая погрешность вычисления местоположения пункта Р по трем направлениям вычисляется при помощи выражения:

Оценивается точность обратной угловой засечки по способу Кнейссля с определением погрешности:

Допустимость в расхождениях полученных значений двух вариантов решений выполняется по формуле:

Если данное условие соблюдено, то итоговое значение координат берется как среднее арифметическое значение из результатов двух решений.

Уравнивание при помощи параметрического способа

Под определение обратной многократной угловой засечки попадает как совокупность простых однократных измерений, так и просто большое количество избыточных. Однако в обоих случаях необходимо уравнивание, которое выполняется по измеренным углам и направлениям.

К примеру, неизвестные \(x_

\) и \(y_

\) – координаты точки Р, которые в данном способе будут представлены в качестве параметров. Для этого их представляют в виде приближенных значений \(x_<0>\), \(y_<0>\) и поправок к ним \(δх\) и \(δу\).

В приведенном уравнении \(x_<0>\) и \(y_<0>\) – результаты обработки однократных засечек, а \(δх\) и \(δу\) получают через уравнивание методом наименьших квадратов параметрическим способом с применением дифференциальных формул.

Этот метод подразумевает применение не только параметрического, но и коррелатного способа. Они дают одинаковые результаты, но отличаются по объему вычислений.

Однако в геодезической практике целесообразнее применять параметрический способ, поскольку при любом количестве избыточных измерений число нормальных уравнений будет аналогично числу неизвестных. При этом каждое неизвестное будет представлено в виде суммы приближенного значения и его поправки.

Сферы применения

Обратная угловая засечка нашла широкое применение в строительстве высотных зданий и сооружений, вроде опорных конструкций для мостов и дымовых труб. Кроем того, она позволяет быстро построить строительную сетку или определить местоположение точки в пространстве. В геодезии ее нередко используют в трилатерации и триангуляции.

Нельзя также не упомянуть ее огромного практического значения в навигации и военном деле. В частности, засечка по обратным дирекционным углам используется для топографогеодезической подготовки командно-наблюдательного пункта и позиции ведения огня.

Источник

Обратная линейно угловая засечка тахеометром SOKKIA серии CX

Геодезическая засечка или просто засечка это — способ получения информации о координатах расположения точки путём измерения углов и расстояний от этой точки до известных ориентиров (пунктов опорной геодезической сети), который широко используется в практике геофизических, геологических, инженерных, строительных и др. работ.
Определение координат станции методом обратной засечки
Ввод Вывод
Координаты известной точки : (Xi,Yi, Zi) Координаты станции : (X0,Y0, Z0)
Измеренный горизонтальный угол : Hi
Измеренный вертикальный угол : Vi
Измеренное расстояние : Di

По результатам наблюдений известных точек вычисляются либо все координаты станции (X, У, Н), либо только высотная компонента Н.
В случае координатной засечки полученные значения замещают введенные или измеренные ранее координаты станции (X, Y, Н) однако в случае высотной засечки замещается только значение Н. Всегда выполняйте измерения в последовательности, описанной в разделах
“Координатная засечка” и “Высотная засечка».
Введенные координаты известных точек и вычисленные данные точки стояния могут быть записаны в выбранный файл работы.
«ВЫБОР И УДАЛЕНИЕ ФАЙЛА РАБОТЫ»
При выполнении линейных измерений можно использовать от 2 до 10 известных пунктов, а при выполнении угловых измерений — от 3 до 10.
1. В экране координатных измерений выберите «Ввод СТН».
2. Нажмите клавишу [ЗАСЕЧ]
3. Выберите “XYH”.
4. Наведитесь на первую известную точку и нажмите [ИЗМЕР] для запуска измерений. Результаты измерений выводятся на экран.
Если была нажата клавиша [УГОЛ], расстояние на экран не выводится.

5. Нажмите клавишу [ДА], чтобы использовать результаты измерений на первую известную точку.
Здесь также можно ввести высоту отражателя.

6. Введите координаты 1-й известной точки и нажмите [СЛЕД], чтобы перейти ко 2-й известной точке.
Если нажать клавишу [СЧИТ], то можно использовать записанные в памяти координаты.

Для возврата к предыдущей точке нажмите .
7. Аналогичным образом повторите шаги 4-6 для второй точки. Когда количество измеренных точек будет достаточно для вычисления координат станции, появится клавиша [ВЫЧ].
8. После окончания наблюдений всех известных точек нажмите [ВЫЧ] для автоматического запуска процесса вычислений. На экране отображаются координаты станции и значения стандартных отклонений, характеризующие точность измерений.

9. Нажмите [РЕЗ-Т] для просмотра результатов.
Если проблем с результатами нет, нажмите для возврата в предыдущий экран.
Если имеется известная точка, которая не была измерена, или если требуется добавить новую известную точку, нажмите <ДОБ>.

10. Если есть сомнения относительно результатов измерений на какую-либо точку, поставьте курсор на нужную строку и нажмите клавишу [ПЛОХ]. Слева от номера точки появится символ»*”. Повторите процедуру для всех проблемных точек.

11. Нажмите клавишу [П-Выч] для выполнения повторных вычислений без использования точек, помеченных на шаге 10. Результат вычислений отображается на экране. Если результаты не вызывают сомнений, переходите к шагу 12. Если снова возникли проблемы, повторите действия с шага 4.
Нажмите клавишу [П_Набл.> для наблюдения точки, помеченной на шаге 10. Если на шаге 10 точки не помечены, то можно повторить наблюдения на все точки или только на последнюю измеренную точку.

12. Нажмите [ДА] в экране шага 9, чтобы завершить измерения. Координаты станции определены. Нажмите [ДА], если хотите установить дирекционный угол на 1 -ю известную точку как на точку обратного ориентирования (за исключением помеченных точек). Отображается экран настройки станции. Нажатие клавиши [ДА] задает дирекционный угол и координаты станции, после чего отображается экран .

13. При нажатии [ЗАП] отображается экран измерений на точку обратного ориентирования.
Нажмите [ДА], чтобы сохранить: координаты станции, измерения на точку обратного ориентирования, координаты известной точки и результаты угловых измерений (результаты измерения расстояний сохраняются при нажатии клавиши [ИЗМЕР]).

Чтобы вернуться в экран настройки станции без установки дирекционного угла, нажмите [НЕТ]. Отсюда повторите процедуру установки дирекционного угла.

Если в режиме настроек выбрана единица измерения “дюйм”, то стандартное отклонение отображается в “футах” или «футах США» в зависимости от того, какой именно фут был выбран ранее.

Высотная засечка

В результате засечки определяется только координата Н (высота) станции.
Для известных точек должно быть измерено только расстояние.
Для измерений можно использовать от 1 до 10 известных точек.
1. В экране координатных измерений выберите «Ввод СТН».
2. В открывшемся окне нажмите клавишу [ЗАСЕЧ].
3. Выберите “Высота”. Если инструмент находится вне диапазона работы компенсатора, выводится соотвествующий экран. Приведите инструмент к горизонту.

4. Наведитесь на 1-ю известную точку и нажмите клавишу [ИЗМЕР] для запуска измерений. Чтобы остановить измерения, нажмите [СТОП].
Результаты измерений отображаются на экране.

5. Нажмите клавишу [ДА], чтобы использовать результаты измерений на 1-ю известную точку.

6. Введите координаты известной точки. После ввода высоты первой точки нажмите клавишу [СЛЕД] для перехода ко второй известной точке.
7. При использовании двух и более известных точек повторите действия 4-6 в том же порядке, начиная со второй точки. Для возврата к предыдущей известной точке нажмите .
8. После окончания наблюдений всех известных точек нажмите [ВЫЧ] для автоматического запуска процесса вычислений. На экране отображаются высота станции и значение стандартного отклонения, характеризующие точность измерения.
9. Нажмите [РЕЗ-Т] для просмотра результатов. Если проблем с результатами нет, нажмите клавишу и переходите к шагу 10.

10. Если есть сомнения относительно результатов измерений на какую-либо точку, поставьте курсор на нужную строку и нажмите клавишу [ПЛОХ]. Слева от номера точки появится символ»*».
11. Нажмите клавишу [П-Выч] для выполнения повторных вычислений без использования точек, помеченных на шаге 10. Результат вычислений отображается на экране. Если результаты не вызывают сомнений, переходите к шагу 12. Если снова возникли проблемы, повторите действия с шага 4.
12. Чтобы завершить измерения, нажмите [ДА]. Устанавливается только координата Н станции. Координаты X и Y станции не перезаписываются.
Процесс вычисления обратной засечки
Тахеометр определяет плановые координаты X и У, используя уравнения наблюдений углов и расстояний, при этом плановые координаты станции вычиляются с использованием метода наименьших квадратов. Координата Н станции рассчитывается путем усреднения значений координаты Н станции, полученных из наблюдений каждой известной точки.

О чем следует помнить при выполнении обратной засечки
В некоторых случаях невозможно вычислить координаты неизвестной точки (станции), если эта точка и три или более известных пунктов лежат на одной окружности.

Желательно, чтобы точки были расположены по отношению друг к другу, как указано ниже.

Иногда невозможно правильно выполнить вычисление, например, в ситуации, показанной ниже.

Когда точки находятся на одной окружности, предпримите одно из следующих действий.
(1) Переместите точку стояния как можно ближе к центру треугольника.
(2) Отнаблюдайте еще одну известную точку, не лежащую на этой окружности.
(3) Выполните измерение расстояния, по крайней мере, на одну из этих трех точек.

В некоторых случаях невозможно вычислить координаты станции, если угол, заключенный между известными точками, слишком мал. Чем больше расстояние между точкой стояния и известными точками, тем острее заключенный между известными точками угол. Будьте внимательны, поскольку известные точки могут находиться на одной окружности.

Источник