Способ обозначения выражения чисел

Способ выражения и обозначения чисел

Последняя бука буква «е»

Ответ на вопрос «Способ выражения и обозначения чисел «, 9 (девять) букв:
счисление

Альтернативные вопросы в кроссвордах для слова счисление

Определение слова счисление в словарях

Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
СЧИСЛЕНИЕ (нумерация) способ выражения и обозначения чисел. В системах счисления некоторое число n единиц (напр., десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д.

Большая Советская Энциклопедия Значение слова в словаре Большая Советская Энциклопедия
нумерация, совокупность приёмов наименования и обозначения чисел. Наиболее совершенным принципом представления чисел является позиционный (поместный) принцип, согласно которому один и тот же числовой знак ( цифра ) имеет различные значения в зависимости.

Примеры употребления слова счисление в литературе.

Из-за густого снега и сплошной облачности пришлось полагаться на счисление: когда в пост управления зенитным огнем угодил снаряд, автопрокладчик вышел из строя.

Мало того, разделив счисление на алгебраическое и арифметическое, Конт допускает — как он необходимо и должен допустить, — что алгебраическое счисление более обще, чем арифметическое, однако же он не скажет, что алгебра предшествовала арифметике по времени.

Под вечер, в сумерках, когда до губы Белушьей осталось по счислению еще сто двадцать две мили, буксирный трос лопнул.

Основные технические характеристики машины: система счисления — двоичная, форма представления чисел — с фиксированной запятой, разрядность — 36, система команд — одноадресная, быстродействие — 100 операций в 1 сек.

Десять пальцев рук утвердили всю десятеричную систему счисления, по мнению многих, одну из наименее эффективных, поскольку 10 имеет всего два делителя, в отличие скажем от 12, имеющих четыре делителя65.

Источник: библиотека Максима Мошкова

Источник

Способ выражения чисел

Последняя бука буква «е»

Ответ на вопрос «Способ выражения чисел «, 9 (девять) букв:
счисление

Альтернативные вопросы в кроссвордах для слова счисление

Определение слова счисление в словарях

Большая Советская Энциклопедия Значение слова в словаре Большая Советская Энциклопедия
нумерация, совокупность приёмов наименования и обозначения чисел. Наиболее совершенным принципом представления чисел является позиционный (поместный) принцип, согласно которому один и тот же числовой знак ( цифра ) имеет различные значения в зависимости.

Энциклопедический словарь, 1998 г. Значение слова в словаре Энциклопедический словарь, 1998 г.
СЧИСЛЕНИЕ (нумерация) способ выражения и обозначения чисел. В системах счисления некоторое число n единиц (напр., десять) объединяется в одну единицу 2-го разряда (десяток), то же число единиц 2-го разряда объединяется в единицу 3-го разряда (сотню) и т.д.

Примеры употребления слова счисление в литературе.

Из-за густого снега и сплошной облачности пришлось полагаться на счисление: когда в пост управления зенитным огнем угодил снаряд, автопрокладчик вышел из строя.

Мало того, разделив счисление на алгебраическое и арифметическое, Конт допускает — как он необходимо и должен допустить, — что алгебраическое счисление более обще, чем арифметическое, однако же он не скажет, что алгебра предшествовала арифметике по времени.

Под вечер, в сумерках, когда до губы Белушьей осталось по счислению еще сто двадцать две мили, буксирный трос лопнул.

Основные технические характеристики машины: система счисления — двоичная, форма представления чисел — с фиксированной запятой, разрядность — 36, система команд — одноадресная, быстродействие — 100 операций в 1 сек.

Десять пальцев рук утвердили всю десятеричную систему счисления, по мнению многих, одну из наименее эффективных, поскольку 10 имеет всего два делителя, в отличие скажем от 12, имеющих четыре делителя65.

Источник: библиотека Максима Мошкова

Источник

Числовые и буквенные выражения

Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Числовое выражение – это запись , состоящая из чисел и знаков действий между ними.

Например, 44 + 32

Значение выражения — это результат выполненных действий.

Например, в записи 44 + 32 = 76, значение выражения — это 76.

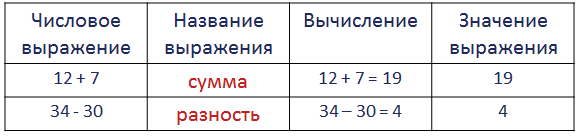
Чтение числовых выражений

49 — 20 — разность

34 — (8 + 21) — из 34 вычесть сумму чисел 8 и 21

13 + (26 — 8) — к 13 прибавить разность чисел 26 и 8

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Давай сравним значения двух выражений: 14 — 6 и 18 — 9.

Для этого найдем значения каждого из них:

Буквенные выражения

Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

В этих выражениях буквы могут обозначать различные числа. Число, которым заменяют букву, называют значением .

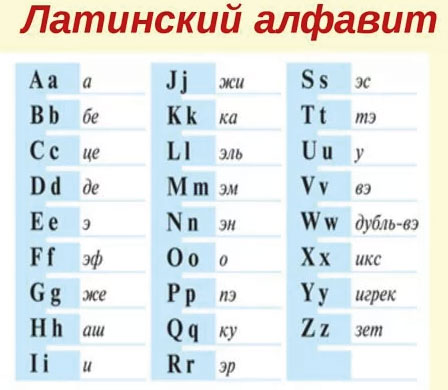
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

Алгоритм — значит, порядок, план выполнения команд.

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Поделись с друзьями в социальных сетях:

Источник

Числовые и буквенные выражения

Числовые выражения

Числовое выражение — это запись, составленная со смыслом, в которой числа обозначены цифрами (в неё также могут входить знаки арифметических действий и скобки). Числовые выражения так же называются арифметическими выражениями.

7 — числовое выражение,

2 + 2 — 1 — числовое выражение,

7 — 2 · + : 1 — бессмысленный набор символов.

Вычислить значение выражения — это значит выполнить все арифметические действия, указанные в выражении. Действия выполняются в определённом порядке, в зависимости от самих действий и присутствия в выражении скобок. Про порядок выполнения действий можно прочитать в теме Порядок действий .

Значение числового выражения — это число, получившееся после выполнения всех вычислений. Например, в выражении

число 8 — это значение числового выражения 6 + 2.

Пример 1. Найдите значение числового выражения 4 + 3.

Пример 2. Вычислите значение числового выражения 4 · 3.

Пример 3. Запишите числовые выражения и найдите их значения.

1) Из числа 60 вычесть сумму чисел 23 и 7.

2) К частному чисел 30 и 6 прибавить 18.

3) Число 93 уменьшить на произведение 5 и 6.

4) Из разности чисел 57 и 7 вычесть число 8.

1) 60 — (23 + 7) = 60 — 30 = 30.

2) 30 : 6 + 18 = 5 + 18 = 23.

3) 93 — 5 · 6 = 93 — 30 = 63.

4) (57 — 7) — 8 = 50 — 8 = 42.

С помощью числовых выражений можно записывать решение задач.

Задача. Из куска шёлка длиной 18 метров сшили 4 платья, расходуя на каждое по 3 метра. Сколько метров шёлка осталось в куске?

Решение: Задача решается в два действия: сначала узнаём сколько шёлка было израсходовано на платья, а затем сколько шёлка осталось. Решение по действиям можно записать так:

1) 3 · 4 = 12 (м) — израсходовали на платья.

2) 18 — 12 = 6 (м) — осталось в куске.

Объединив эти два действия, получим числовое выражение

Значение этого выражения является ответом на вопрос данной задачи.

Буквенные выражения

Буквенное выражение — это числовое выражение, в котором числа могут быть обозначены и цифрами, и буквами. Буквенные выражения так же называются алгебраическими выражениями.

При обозначении чисел буквами обычно используют строчные (маленькие) буквы латинского алфавита:

7 · a — буквенное выражение,

a – (b + c) — буквенное выражение.

Чаще всего в буквенных выражениях разные числа обозначены разными буквами, но, например, в выражении:

подразумевается, что a и b являются одним и тем же числом.

Значение буквенного выражения — это число, получившееся после выполнения всех вычислений. Действия в буквенных выражениях выполняются после подстановки вместо букв их численных значений.

Пример. Найдите значение буквенного выражения 2 · a + 3 при a = 7.

2 · 7 + 3 = 14 + 3 = 17.

Если в записи выражения одна и та же буква, например a, употребляется несколько раз, то под значением этой буквы во всех случаях мы должны иметь ввиду одно и тоже число.

Пример. Найдите значение буквенного выражения 5x — 2x при x = 4.

5 · 4 — 2 · 4 = 20 — 8 = 12.

В арифметике буквенные обозначения употребляют, когда необходимо выразить, что свойство (или правило) относится не к каким-нибудь отдельным числам, а является общим для любых чисел. Например:

Данное равенство показывает нам, что, как бы мы не переставляли слагаемые, сумма от этого не изменится. Подставив вместо букв любые числа, мы можем убедиться в этом сами:

Запись буквенных выражений

При записи буквенных выражений, знак умножения пишется только:

между буквой и числом:

между закрывающей скобкой и следующей за ней буквой или числом:

Знак умножения между числом и буквой, между буквами и перед открывающей скобкой не пишут:

В буквенных выражениях числовой множитель записывается перед буквенными множителями:

Частное двух чисел, обозначенных буквами, обычно записывается с помощью дробной черты, например:

Источник

Числовые, буквенные выражения и выражения с переменными: определения, примеры

В математике принято использовать свои обозначения. Запись условий задач с их помощью приводит к появлению так называемых математических выражений. Можно говорить про числовые, буквенные выражения и математические выражения с переменными. Для удобства и одни, и вторые и третьи называются просто выражениями. В этой статье мы дадим определения и по порядку рассмотрим каждый тип математических выражений.

Числовые выражения

С самый первых уроков математики школьники начинают знакомство с числовыми выражениями. Выражение содержит числа, и действия над этими числами. Возьмем простейшие примеры для счета: 5 + 2 ; 3 — 8 ; 1 + 1 . Все это — числовые выражения. Если выполнить действия, указанные в выражении, то получится его значение.

Конечно, числовые выражения содержат не только знаки «плюс» и «минус». Они могут включать деление и умножение, содержать скобки, степени, корни, логарифмы и состоять из нескольких действий.

Учитывая все сказанное, дадим определение. Что такое числовое выражение?

Определение. Числовое выражение

Числовые выражения — это комбинация чисел, арифметических действий, знаков дробных черт, корней, логарифмов, тригонометрических и других функций, а также скобок и иных математических символов.

Числовым выражением считается только та комбинация, которая составлена с учетом математических правил.

Поясним данное определение.

Во-первых, числа. Математическое выражение может содержать любые числа. Это значит, что в математическом выражении можно встретить:

• натуральные числа: 6 , 173 , 9 ,
• целые числа: 18 , 0 , 64 ,
• рациональные числа:
  обыкновенные дроби 1 3 , 3 4 ,
  смешанные числа 6 1 8 , 89 5 7 ,
  периодические и непериодические десятичные дроби 9 , 78 , 8 , 556
• иррациональные числа: π , e ,
• комплексные числа: i = — 1 .

Во-вторых, арифметические действия. то известные нам еще из курса начальной школы сложение, умножение, вычитание и деление. Знаки » + » , » — » , » · » и » ÷ » могут присутствовать в выражении не один раз. Вот пример такого числового выражения: 12 + 4 — 3 + 3 ÷ 1 · 8 · 6 ÷ 2 .

деление в выражениях может присутствовать как в виде знака, так и в виде дробной черты.

Скобки в числовых выражениях

• указывают порядок выполнения действий: 5 — 2 , 5 + 5 * 0 , 25 ;
• используются для записи отрицательных чисел: 5 + ( — 2 ) ;
• отделяют аргумент функции: sin π 2 — π 3 ;
• отделяют показатель степени: 2 — 1 , 3 2

Есть и специальные значения для записи скобок. Например, запись 1 , 75 + 2 означает, что к целой части числа 1 , 75 прибавляется число 2 .

Согласно определению, числовые выражения могут содержать степени, корни, логарифмы, тригонометрические и обратные тригонометрическим функции. Приведем пример такого числового выражения:

В качестве примера использования в числовых выражениях специальных знаков, можно привести знак модуля.

— 2 2 5 · 6 + — 5 — 8 · 2

Буквенные выражения

После знакомства с числовыми выражениями можно вводить понятие буквенных выражений. Интуитивно понятно, что в них вместо чисел используются буквы. Но обо всем по порядку.

Запишем числовое выражение, но вместо одного числа оставим пустой квадратик.

В квадратик мы можем вписать любое число. Например, 2 , или 1032 .

Если условится записывать вместо числа в квадратике букву a , означающую данное число, то мы получим буквенное выражение:

Определение. Буквенное выражение

Выражение, в котором буквы заменяняют некоторые цифры, называется буквенным выражением. Буквенное выражение должно содержать по крайней мере одну букву.

Принципиальная разница числового и буквенного выражений в том, что первое не может содержать букв. В буквенных выражениях чаще всего используются маленькие буквы латинского алфавита a , b , c . . или маленькие греческие буквы α , β , γ . . и т.д.

Приведем пример сложного буквенного выражения.

x 3 + 2 — 4 · x 5 + 4 x y + 8 y 2 3 8 — 4 x 2 · a r c cos α + 1 3 x 2 + 2 y — 1

Выражения с переменными

В рассмотренных выше буквенных выражениях буква обозначала какое-то конкретное числовое значение. Величина, которая может принимать ряд различных значений, называется переменной. Выражение с такой величиной, соответственно, называются выражением с переменной.

Определение. Выражения с переменными

Выражение с переменной — выражение, в котором все или некоторые буквы обозначают величины, принимающие различные значения.

Пусть переменная x принимает натуральные значения из интервала от 0 до 10 . Тогда выражения x 2 — 1 есть выражение с переменной, а x — переменная в этом выражении.

В выражении может быть не одна, а несколько переменных. Например, при переменных x и y выражение x 3 · y + y 2 2 — 1 представляет собой выражение с двумя переменными.

Вообще буквенные выражения и выражения с переменными позволяют посмотреть на задачу вне контекста конкретных чисел, то есть более широко. Они широко используются в математическом анализе для формулировок и доказательств.

Внешний вид буквенного выражения не позволяет узнать, являются входящие в него буквы переменными, или нет. Для этого нужно знать условия конкретной задачи, описываемой выражением. Вне контекста ничто не мешает считать входящие в выражение буквы переменными. Таким образом, разница между понятиями «буквенное выражение» и «выражение с переменными» нивелируется.

Источник