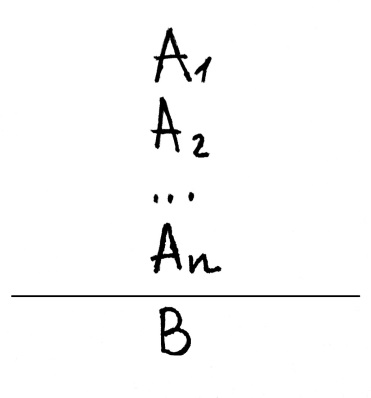Способ обоснования истинности суждения с помощью логических умозаключений

Доказательство – способ обоснования истинности

Получение опосредованных, выводных знаний происходит не только в форме умозаключения. Доказательствостроится на умозаключениях, но не сводится к ним. Открывая истину, человек стремится передать ее другим людям, а для этого он должен убедиться сам в ее истинности, и убедить в этом других. Только так она получает общественное признание.

Доказательство — это рассуждение, устанавливающее истинность какого-либо утверждения путем приведения других утверждений, истинность которых уже не вызывает сомнений. В логике и в повседневной жизни доказательства понимается по-разному. В обыденности под доказательством понимают: факты, с помощью которых обосновывается истинность какого-то положения, т.е. саму действительность. Логика исследует доказательство как мыслительную структуру, форму мысли, конструкцию логически связанных между собой нескольких мыслей, обосновывающих исходную мысль. По форме оно сложнее, чем умозаключение, состоит порой из нескольких умозаключений. Отличие от умозаключения и в том что оно предназначено для выведения новых знаний, а доказательство для установки истинность или ложность того или иного знания, оно служат важным средством формирования убеждений — уверенности в правоте тех или иных знаний.

В действительности немногие истины являются самоочевидными и не требующими доказательств. К ним относятся истины факта, получаемые с помощью органов чувств; аксиомы (ценный, бесспорный, заслуживающий доверия), в истинности которых убеждает вся предшествующая практика человечества; постулаты, положения, принимаемые на веру. Грань между не доказываемыми и доказываемыми положениями подвижна, условна, относительна, с одной стороны, с ростом знаний растет и число аксиом, а с другой — наука всемерно стремится сузить их число, доказать.

Эмпирические и дедуктивные доказательства

Различают доказательства дедуктивного и индуктивного характера. Дедуктивные доказательства более распространены в математике, теоретической физике, философии и других науках, имеющих дело с неспецифицированными объектами, с объектами, не воспринимаемыми непосредственно. Индуктивные доказательства — в опытных, экспериментальных, прикладного характера науках.

Структура доказательства

Во всяком доказательстве различают три части: доказываемое положение, или тезис — то, что должно быть доказано или сделано очевидным, выражается в форме суждения; основание доказательства, или аргументы; — то, при помощи чего тезис доказывается или делается очевидным; демонстрация — форма доказательства, или способ, каким тезис выводится из аргументов. Тезис — соответствует заключению в силлогизме, аргументы – посылкам. Демонстрация — логическая схема, при помощи которой выводится заключение. Аргументы и тезис, поскольку они суждения, могут связываться между собой либо по фигурам категорического силлогизма, либо по правильным модусам условных, разделительных и условно-разделительных силлогизмов.

При сопоставлении структурных элементов доказательства и умозаключения, видно их сходство и различие. Простейшее доказательство может выглядеть в виде одного, как бы перевернутого умозаключения, например, простого категорического. Тезисом в этом доказательстве будет то суждение, которое в силлогизме является выводом. Аргументами будут выступать посылки умозаключения, а демонстрацией — логическая связь между посылками, обуславливающая возможность вывода-тезиса.

Пример: доказать, что «Железо плавится» — это тезис.

Для доказательства воспользуемся двумя аргументами: «Все металлы плавятся» и «Железо — металл». Построив силлогизм, мы докажем наш тезис.

Самое трудное в доказательстве — показать, что между аргументами и тезисом существует определенная логическая связь, что тезис действительно вытекает из приведенных аргументов. В повседневной жизни часто, высказав некоторые аргументы, человек присоединяет к ним свой тезис с помощью слов «таким образом», «поэтому», «итак», «следовательно» и т.п. Но эти слова не создают логической связи между аргументами и тезисом. Если в действительности такой связи нет, то она и не появится от этих слов. Доказательство безупречно тогда, когда рассуждениям придается вид определенного умозаключения. Если нужно доказать тезис «Этот проводник нагревается», то аргументами будут суждения: «Если по проводнику проходит электрический ток, то он нагревается» — физический закон — и «По этому проводнику проходит электрический ток» — установленный факт. Из них по утверждающему модусу условно-категорического силлогизма выводим тезис: «Следовательно, этот проводник нагревается».

Но не всегда связь аргументов с тезисом представлена в виде умозаключения, часто она усматривается интуитивно и важно то, чтобы эта связь действительно существовала.

Прямое и косвенное доказательство

По способу проведения доказательства делятся на два вида, прямое (прогрессивное) и косвенное (регрессивное). При прямом доказательстве задача состоит в том, чтобы найти такие убедительные аргументы, из которых логически вытекает тезис, и тезис непосредственно следует из аргументов. Косвенное доказательство имеет более сложную структуру. К элементам доказательства добавляется еще один элемент — антитезис, утверждение, противоречащее тезису, а затем показывается, что он ложен, т.е. устанавливается справедливость тезиса тем, что вскрывается ошибочность противопоставляемого допущения. Это дает право утверждать, что тезис истинен. Такое косвенное доказательство называют «доказательством от противного». Другая разновидность косвенного доказательства – «разделительное», когда из нескольких возможных тезисов методом исключения доказывается один, т.е. путем исключения всех членов разделительного суждения по разделительно-категорическому силлогизму, кроме нашего тезиса, являющегося одним из членов этого разделительного суждения. Данный вид доказательства будет осуществляться по разделительно-категорическому или условно-разделительному силлогизму.

В этих случаях необходимо опираться на требования логики к этим формам мысли, на законы, строго соблюдать их. При формулировке антитезиса необходимо, чтобы он был действительно противоречащим тезису, а не противоположным ему, потому что противоречие не допускает одновременной ни истинности, ни ложности этих суждений, а противоположность допускает их одновременную ложность, поэтому обоснование ложности противоположного тезису суждения, не гарантирует истинность тезиса. Косвенными доказательствами пользуются тогда, когда нет аргументов для прямого доказательства, когда невозможно обосновать тезис прямо. При разделительном косвенном доказательстве, необходимо соблюдать все требования логики к разделительному суждению, к процессу деления объема данной предметной области, а именно главные требования логики к делению — расчленение по одному основанию деления, последовательно (без скачков, пропусков), полно, соразмерно и чтобы члены деления исключали друг друга.

Пример: доказать, что «сумма углов четырехугольника равна 360°».

Доказательство: разделим четырехугольник на два треугольника, следовательно, сумма его углов равна сумме углов двух треугольников. Известно, что сумма углов треугольника составляет 180°, поэтому сумма углов четырехугольника равна 360°.

Пример: построить косвенное доказательство тезиса: «Квадрат не является окружностью».

Выдвигается антитезис: «Квадрат является окружностью» и покажем, что он ложный. Выводим из него следствия, и если хотя бы одно из них, окажется ложным, это будет означать, что и само утверждение, также ложно. Неверным является следствие: «У квадрата нет углов». Поскольку антитезис ложен, исходный тезис должен быть истинным.

Опровержение

Опровержение — это отрицание доказательства, обоснование ложности или несостоятельности либо элементов, либо доказательства в целом. Опровержение структурно мало чем отличается от доказательства. Оно может быть направлено против тезиса доказательства, против аргументов его, против демонстрации. Опровергая тезис — формулирует антитезис; опровергая аргументы — выдвигает другие; опровергая демонстрацию доказательства — показывает строгое соблюдение логических связей между своими аргументами и антитезисом.

Обоснование истинности антитезиса рассматривается и как доказательство антитезиса, и как опровержение тезиса. Обоснование несостоятельности аргументов — не доказывает ложности тезиса, а указывает на недостаточность приведенных аргументов, лишь отвергает их. Т. о., опровержение аргументов не всегда можно назвать антидоказательством.

Опровергая демонстрацию, обосновывая неправильность, нелогичность связи тезиса с аргументами, указывают на нарушение логики, но этим не отрицается сам тезис и аргументы. И то, и другое может оказаться приемлемым, если найти более правильные непосредственные или опосредованные связи между ними, поэтому, не всякое опровержение отбрасывает доказательство в целом.

Видам опровержения (опровержение тезиса, аргументов и демонстрации) соответствуют и способы опровержения. Тезис можно опровергнуть путем доказательства антитезиса и путем выведения следствий из тезиса, противоречащих действительности. Аргументы можно опровергнуть как путем обоснования их ложности, так и тем, что для доказательства тезиса приведенных аргументов мало и они сами нуждаются в обосновании.

Примеры: Закон сохранения и превращения энергии в физике, опровергающие возможность создания вечного двигателя; в биологии Ч. Дарвин эволюционным учением опроверг линнеевский тезис о неизменности видов животных и растений («Видов столько, сколько их создал Бог»).

Требование к элементам доказательства

Обсуждение различных вопросов в обыденной жизни, так и научные рассуждения, приводят к истинным результатам, если соблюдены правила аргументации по отношению к тезису, аргументам, демонстрации.

Правила тезиса

Доказуемый тезис должен быть истинным, истинность тезиса не рождается, а лишь устанавливается, раскрывается. Все попытки нарушить это правило, которое вытекает из самой сущности истины как соответствия мысли действительности, завершались неудачей.

Тезис должен быть четко и ясно сформулирован, без двусмысленности, противоречивости. Описание тезиса с помощью новых терминов допустимо, но необходимо четко выявить их смысл через раскрытие содержания понятий.Четкое определение тезиса наряду с выявлением смысла употребляемых терминов включает анализ суждения, в форме которого выставляется тезис.

Если тезис — простое суждение, то нужно выявить Sи P, уяснить качество (отрицание или утверждение) и количество (общее или частное), а так же выяснить, является оно неопределенным(«некоторые, а может быть, и все») или определенным(«только некоторые») частным суждением.

Пример: «Люди — эгоисты» или «Люди самонадеянны».

Здесь не ясно — обо всех или о некоторых людях идет речь. Такого рода тезисы трудно отстаивать и трудно опровергать.

Если тезис — сложное суждение, то нужен дополнительный анализ логических связок. Предполагается его расчленение на относительно самостоятельные части с выделением существенных элементов, которые выполняют роль основных пунктов разногласия, что позволяет поэтапно обсуждать тезис — принимать или отвергать важнейшие его элементы.

Тезис на всем протяжении доказательства должен оставаться одним и тем же. Правило неизменности тезиса запрещает отступать от первоначально сформулированного положения в процессе рассуждения. Если под влиянием новых фактов выясняется, что тезис неточный, то его можно изменить, при этом необходимо оппонента поставить в известность. Негласное отступление от первоначального тезиса запрещается.

Правила аргументов

Аргументы должны быть истинными и их истинность не должна вызывать сомнений.Это правило неразрывно связано

с первым правилом тезиса.

Истинность аргументов должна устанавливаться автономно, т.е. независимо от доказываемого тезиса. Иначе может получиться, что недоказанным тезисом обосновываются недоказанные аргументы.

Аргументы должна быть непротиворечивыми. Если один из ваших аргументов противоречит другому, то, хотя бы один из них ложен. Содержательно из противоречивых оснований с необходимостью не вытекает ни одно положение.

Каждый аргумент должен быть необходимым и достаточным для вывода тезиса. Один аргумент почти никогда не дает обоснования тезиса, его доказательная сила мала. Но несколько взаимосвязанных аргументов способны создать логическую основу для вывода. Правило достаточности аргументов проявляется по-разному, в зависимости от видов умозаключений, при аналогии проявляется в малом числе сходных признаков, неубедительно и индуктивное обобщение, если исследованные случаи не отражают особенностей образца.

Правила демонстрации

Логическая связь аргументов с тезисом протекает в форме таких умозаключений, как дедукция, индукция и аналогия, поэтому правила демонстрации сводятся к соблюдению правил соответствующих умозаключений.

Источник

Урок 6. Умозаключения

В этом уроке мы, наконец, переходим к теме, которая составляет ядро любого рассуждения и любой логической системы – умозаключениям. В четвёртом уроке мы говорили, что рассуждение – это совокупность суждений или высказываний. Очевидно, что такое определение не полно, ведь оно ничего не говорит о том, почему вдруг какие-то разные высказывания оказались рядом. Если дать более точное определение, то рассуждение – это процесс обоснования какого-либо высказывания с помощью его последовательного вывода из других высказываний. Этот вывод чаще всего осуществляется в форме умозаключений.

Содержание:

Умозаключение – это непосредственный переход от одного или нескольких высказываний А₁, А₂, …, А_n к высказыванию В. А₁, А₂, …, А_n называют посылками. Посылка может быть одна, их может быть две, три, четыре, в принципе – сколько угодно. В посылках содержится известная нам информация. В – это заключение. В заключении находится уже новая информация, которую мы извлекли из посылок с помощью специальных процедур. Эта новая информация уже содержалась в посылках, но в скрытом виде. Так вот задача умозаключения сделать это скрытое явным. Кроме того, иногда посылки называют аргументами, а заключение – тезисом, а само умозаключение в этом случае называют обоснованием. Разница между умозаключением и обоснованием состоит в том, что в первом случае, мы не знаем, к какому заключению мы придём, а во втором – тезис нам уже известен, мы просто хотим установить его связь с посылками-аргументами.

В качестве иллюстрации умозаключения можно взять рассуждения Эркюля Пуаро из «Убийства в восточном экспрессе» Агаты Кристи:

Перебрав в уме еще раз показания пассажиров, я пришел к весьма любопытным результатам. Для начала возьмем показания мистера Маккуина. Первая беседа с ним не вызвала у меня никаких подозрений. Но во время второй он обронил небезынтересную фразу. Я сообщил ему, что мы нашли записку, в которой упоминается о деле Армстронгов. Он сказал: «А разве…» – осекся и, помолчав, добавил: «Ну это самое… неужели старик поступил так опрометчиво?…»

Но я почувствовал, что он перестроился на ходу. Предположим, он хотел сказать: «А разве ее не сожгли?» Следовательно, Маккуин знал и о записке, и о том, что ее сожгли, или, говоря другими словами, он был убийцей или пособником убийцы.

Логики записывают умозаключения следующим образом:

Над чертой располагаются посылки, под чертой – заключение, а сама черта обозначает отношение логического следования.

Критерии истинности умозаключений

Также как и для суждений, для умозаключений существуют определённые условия их истинности. При определении, истинное умозаключение или ложное, нужно обращать внимание на два аспекта. Первый аспект – это истинность посылок. Если хотя бы одна из посылок ложна, то и сделанное заключение тоже будет ложным. Поскольку заключение – это та информация, которая была скрыта в посылках и которую мы просто извлекли на свет, то из неверных посылок невозможно случайно получить верный вывод. Это можно сравнить с попыткой сделать бифштекс из моркови. Наверное, моркови можно придать цвет и форму бифштекса, но внутри всё равно будет морковь, а не мясо. Никакие кулинарные операции не преобразуют одно в другое.

Второй аспект – это правильность самого умозаключения с точки зрения его логической формы. Дело в том, что истинность посылок – это важное, но недостаточное условие для того, чтобы заключение было правильным. Нередки ситуации, когда посылки истинны, но заключение неверно. В качестве примера неправильного умозаключения при истинности посылок можно привести умозаключение голубки из «Алисы в стране чудес» Кэрролла. Голубка обвиняет Алису, в том, что она не змея. Вот как она приходит к этому выводу:

Змеи едят яйца.
Девочки едят яйца.
Значит, девочки – это змеи.

Хотя посылки правильные, заключение абсурдно. Умозаключение в целом сделано неверно. Чтобы избежать подобных ошибок, логики выявили такие умозаключения, логические формы которых при истинности посылок гарантируют истинность заключения. Их принято называть правильными умозаключениями. Таким образом, чтобы умозаключение было сделано верно, нужно следить за истинностью посылок и за правильностью самой формы умозаключения.

Мы рассмотрим различные формы правильных умозаключений на примере силлогистики. В этом уроке мы разберём самые простые однопосылочные заключения. В следующем уроке – более сложные заключения: силлогизмы, энтимемы, многопосылочные заключения.

Умозаключения по логическому квадрату

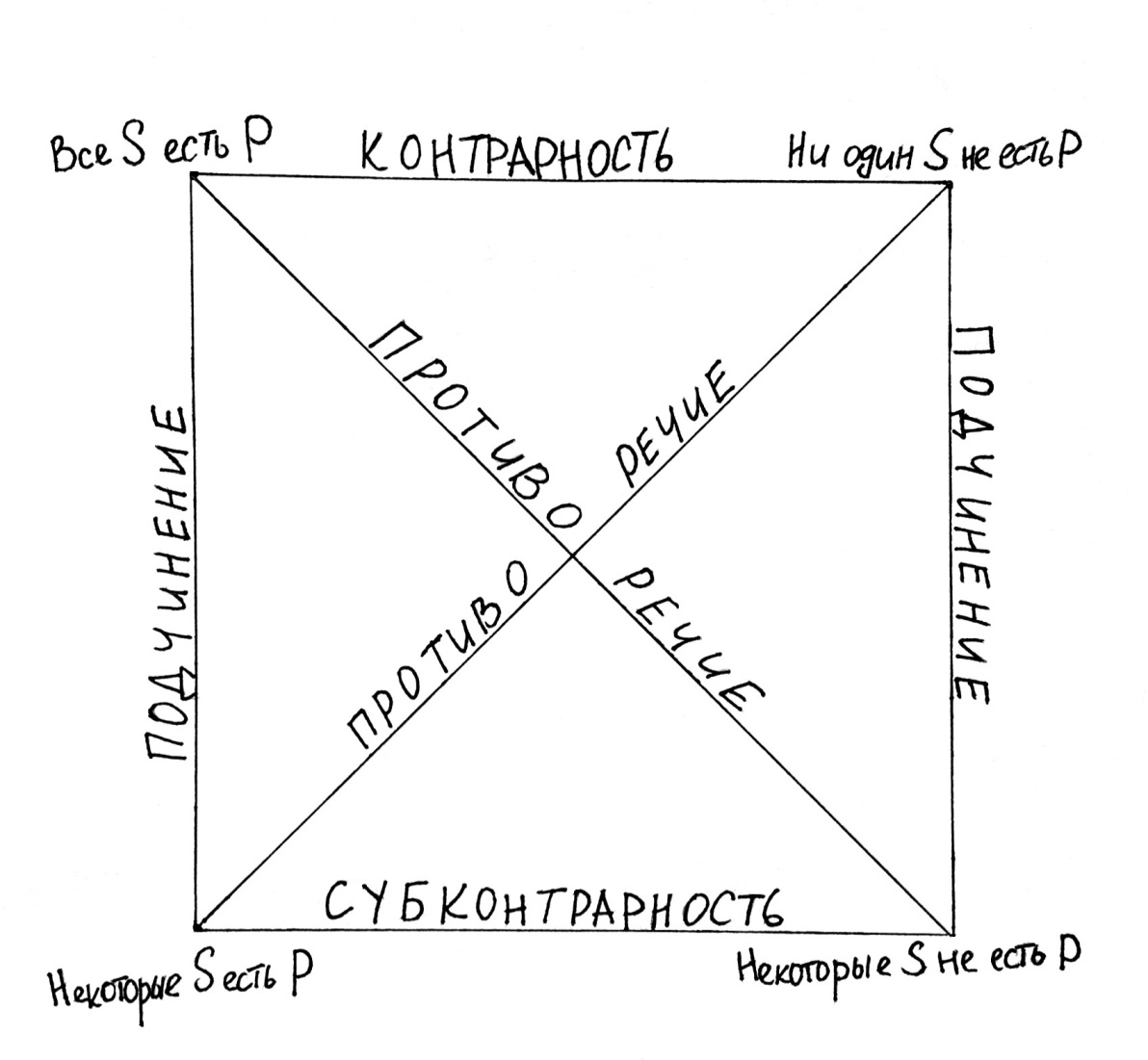
Чтобы было легче запомнить, какие именно типы умозаключений возможны между категорическими атрибутивными высказываниями, логики придумали специальный логический квадрат, изображающий отношения между ними. Поэтому некоторые однопосылочные умозаключения также называют умозаключениями по логическому квадрату. Посмотрим на этот квадрат:

Начнём с отношений подчинения. Мы уже сталкивались с ними в четвёртом уроке, когда рассматривали условия истинности для частно-утвердительных и частно-отрицательных высказываний. Мы говорили, что из высказывания «Все S есть P» будет логичным вывести высказывание «Некоторые S есть P», а из высказывания «Ни один S не есть P» – «Некоторые S не есть P». Таким образом, возможны следующие типы умозаключений:

• Все S есть P
• Некоторые S есть P
• Все птицы имеют клюв. Следовательно, некоторые птицы имеют клюв.
• Ни один S не есть P
• Некоторые S не есть P
• Ни один гусь не хочет быть пойман и зажарен. Следовательно, некоторые гуси не хотят быть пойманными и зажаренными.

Кроме того, по правилу контрапозиции из отношений подчинения можно вывести ещё два правильных умозаключения. Правило контрапозиции – это логический закон, который гласит: если из высказывания А следует высказывание В, то из высказывания «неверно, что В» будет следовать высказывание «неверно, что А». Вы можете попробовать проверить этот закон с помощью таблицы истинности. Итак, будут верны и следующие умозаключения по контрапозиции:

• Неверно, что некоторые S есть P
• Неверно, что все S есть P
• Неверно, что некоторые автомобили не имеют колёс. Поэтому неверно, что все автомобили не имеют колёс.
• Неверно, что некоторые S не есть P
• Неверно, что все S не есть P
• Неверно, что некоторые вина не являются спиртными напитками. Таким образом, неверно, что все вина не являются спиртными напитками.

Отношение контрарности (противоположности) означает, что высказывания типа «Все S есть P» и «Ни один S не есть P» не могут быть одновременно истинными, но они могут быть одновременно ложными. Это хорошо видно из таблицы истинности для категоричных атрибутивных высказываний, которую мы построили в прошлом уроке. Отсюда можно вывести так называемый закон контрарного противоречия: Неверно, что все S есть P и в то же время ни один S не есть P.

По закону контрарного противоречия будут истинными следующие виды умозаключений:

• Все S есть P
• Неверно, что ни один S не есть P
• Все яблоки – это фрукты. Следовательно, неверно, что ни одно яблоко не является фруктом.
• Ни один S не есть P
• Неверно, что все S есть P
• Ни один кит не умеет летать. Поэтому неверно, что все киты умеют летать.

Отношения субконтрарности (подпротивоположности) означают, что высказывания типа «Некоторые S есть P» и «Некоторые S не есть P» не могут быть одновременно ложными, хотя могут быть одновременно истинными. На этом основании может быть сформулирован закон субконтрарного исключённого третьего: Некоторые S не есть P или Некоторые S есть P.

• Согласно этому закону правильными будут следующие умозаключения:
• Неверно, что некоторые S есть P
• Некоторые S не есть P
• Неверно, что некоторые продукты полезны для здоровья. Поэтому некоторые продукты не полезны для здоровья.
• Неверно, что некоторые S не есть P
• Некоторые S есть P
• Неверно, что некоторые ученики из нашего класса не являются двоечниками. Таким образом, некоторые ученики из нашего класса являются двоечниками.

Отношения противоречия (контрадикторности) говорят о том, что высказывания, находящиеся в них, не могут быть одновременно истинными или ложными. На основании этих отношений можно сформулировать два закона противоречия и два закона исключённого третьего. Первый закон противоречия: Неверно, что все S есть P и некоторые S не есть P. Второй закон противоречия: Неверно, что ни один S не есть P и некоторые S есть P. Первый закон исключённого третьего: Все S есть P или некоторые S не есть P. Второй закон исключённого третьего: Ни один S не есть P или некоторые S есть P.

На этих законах строятся умозаключения следующих видов:

• Все S есть P
• Неверно, что некоторые S не есть P
• Все дети нуждаются в заботе. Следовательно, неверно, что некоторые дети не нуждаются в заботе.
• Некоторые S не есть P
• Неверно, что все S есть P
• Некоторые книги не являются скучными. Поэтому, неверно, что все книги являются скучными.
• Неверно, что все S есть P
• Некоторые S не есть P
• Неверно, что все сотрудники нашей фирмы усердно работают. Таким образом, некоторые сотрудники нашей фирмы не работают усердно.
• Неверно, что некоторые S не есть P
• Все S есть P
• Неверно, что некоторые зебры не имеют полосок на коже. Следовательно, все зебры имеют полоски на коже.
• Ни один S не есть P
• Неверно, что некоторые S есть P
• Ни одна картина в этом зале не относится к XX веку. Поэтому неверно, что некоторые картины в этом зале относятся к XX веку.
• Некоторые S есть P
• Неверно, что ни один S не есть P
• Некоторые студенты занимаются спортом. Таким образом, неверно, что ни один студент не занимается спортом.
• Неверно, что ни один S не есть P
• Некоторые S есть P
• Неверно, что ни один учёный не интересуется искусством. Следовательно, некоторые учёные интересуются искусством.
• Неверно, что некоторые S есть P
• Ни один S не есть P
• Неверно, что некоторые коты курят сигары. Таким образом, ни один кот не курит сигары.

Как вы, скорее всего, заметили во всех этих умозаключениях, высказывания над чертой и под чертой несут одну и ту же информацию, просто поданную в разной форме. Важная деталь заключается в том, что смысл одних из этих высказываний воспринимается легко и интуитивно, в то время как смысл других тёмен, и над ними порой приходится поломать голову. Например, смысл утвердительных высказываний воспринимается легче, чем смысл отрицательных высказываний, смысл высказываний с одним отрицанием более понятен, чем смысл высказываний с двумя отрицаниями. Таким образом, основное назначение умозаключений по логическому квадрату состоит в том, чтобы привести сложные для восприятия, непонятные высказывания к наиболее простой и ясной форме.

Операция обращения

Ещё одним видом однопосылочных умозаключений является обращение. Это такой тип умозаключений, при которых субъект посылки совпадает с предикатом заключения, а субъект заключения совпадает с предикатом посылки. Грубо говоря, в заключении S и P просто меняются местами.

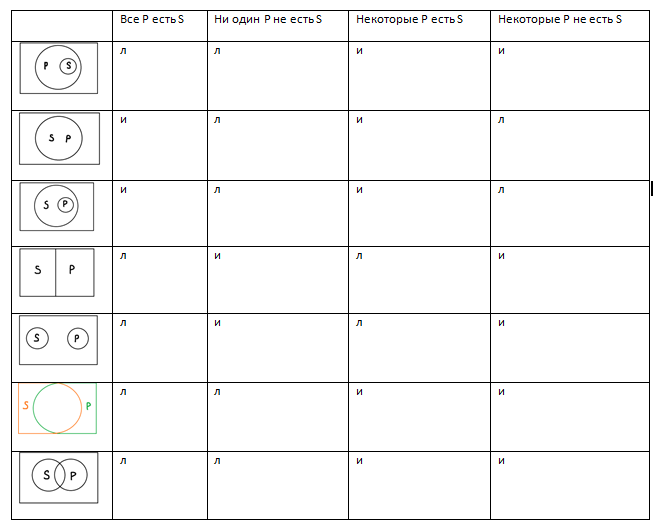
Прежде чем перейти к умозаключениям через обращение, построим таблицу истинности для высказываний, в которых P встанет на место субъекта, а S – на место предиката.

Сравните её с той таблицей, которую мы строили в прошлом уроке. Обращение, как и другие умозаключения, может быть правильным, только когда посылка и заключение одновременно истинны. При сравнении двух таблиц, вы увидите, что таких комбинаций не так уж и много.

Итак, существует два вида обращения: чистое и с ограничением. Чистое обращение происходит тогда, когда количественная характеристика не изменяется, то есть если в посылке было слово «все», то и в заключении тоже будет слова «все»/«ни один», если в посылке слово «некоторые», то и в заключении «некоторые. Соответственно, при обращении с ограничением количественная характеристика меняется: были «все», а стали «некоторые». Для высказываний типа «Ни один S не есть P» и «Некоторые S есть P» правильным будет следующее чистое обращение:

• Ни один S не есть P
• Ни один P не есть S
• Ни один человек не может выжить без воздуха. Следовательно, ни одно живое существо, способное выжить без воздуха, не является человеком.
• Некоторые S есть P
• Некоторые P есть S
• Некоторые змеи ядовиты. Поэтому, некоторые ядовитые существа – это змеи.
• Для высказываний типа «Все S есть P» и «Ни один S не есть P» верно обращение с ограничением:
• Все S есть P
• Некоторые P есть S
• Все пингвины – это птицы. Таким образом, некоторые птицы – это пингвины.
• Ни один S не есть P
• Некоторый P не есть S
• Ни один крокодил не ест зефир. Следовательно, некоторые существа, едящие зефир, не являются крокодилами.
• Высказывания типа «Некоторые S не есть P» вообще не обращаются.

Хотя обращения, как и умозаключения по логическому квадрату, это однопосылочные умозаключения, и мы точно также извлекаем всю новую информацию из имеющейся посылки, посылку и заключение в них уже нельзя назвать просто разными формулировками одной и той же информации. Полученная информация относится уже к другому субъекту, а потому она уже не кажется такой тривиальной.

Итак, в этом уроке мы начали рассматривать правильные виды умозаключений. Мы поговорили о самых простейших однопосылочных умозаключениях: умозаключениях по логическому квадрату и умозаключениях через обращение. Хотя эти умозаключения довольно просты и даже где-то тривиальны, люди повсеместно совершают в них ошибки. Понятно, что сложно удержать в памяти все виды правильных умозаключений, поэтому, когда вы будете выполнять упражнения или столкнётесь с необходимостью проверить или сделать однопосылочное умозаключение в реальной жизни, не бойтесь прибегать к помощи модельных схем и таблиц истинности. Они помогут вам проверить, всегда ли при истинности посылок заключение тоже истинное, а это главное для правильного умозаключения.

Упражнение «Подберите ключ»

В этой игре вам нужно создать ключ правильной формы. Для этого установите засечки нужной длины (от 1 до 3, 0 – быть не может), а затем нажмите кнопку «Попробовать». Вам будут даны 2 суждения, сколько засечек выбранной длины присутствуют в ключе (для простоты значение «наличие»), и сколько из выбранных находятся на своём месте (для простоты значение «на месте»). Скорректируйте своё решение и пробуйте, пока не подберёте ключ.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Упражнения

Сделайте все возможные умозаключения из следующих высказываний по логическому квадрату:

• Все медведи на зиму залегают в спячку.
• Неверно, что все люди завистливы.
• Ни один гном не достигает роста в два метра.
• Неверно, что ни один человек не был на Северном полюсе.
• Некоторые люди никогда не видели снега.
• Некоторые автобусы ходят по расписанию.
• Неверно, что некоторые слоны летали на луну.
• Неверно, что некоторые птицы не имеют крыльев.

Сделайте обращения с теми, высказываниями, с которыми это возможно:

• Никто ещё не построил машину времени.
• Некоторые официанты очень назойливы.
• Все профессионалы опытны в своём деле.
• Некоторые книги не имеют твёрдой обложки.

Проверьте, правильно ли сделаны следующие умозаключения:

• Некоторые кролики не носят белые перчатки. Следовательно, некоторые кролики носят белые перчатки.
• Неверно, что никто не был на Луне. Таким образом, некоторые люди были на Луне.
• Все люди смертны. Поэтому все смертные – это люди.
• Некоторые птицы не умеют летать. Следовательно, некоторые существа, не умеющие летать, это птицы.
• Ни один ягнёнок не имеет пристрастия к виски. Следовательно, ни одно существо, имеющее пристрастие к виски, не является ягнёнком.
• Некоторые морские животные млекопитающие. Таким образом, неверно, что ни одно морское животное не является млекопитающим.

Проверьте свои знания

Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник