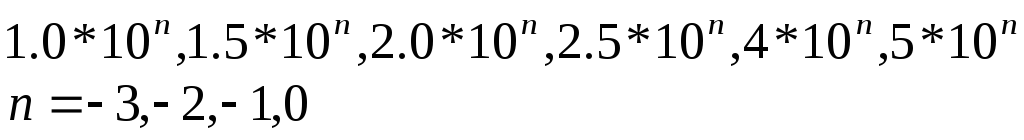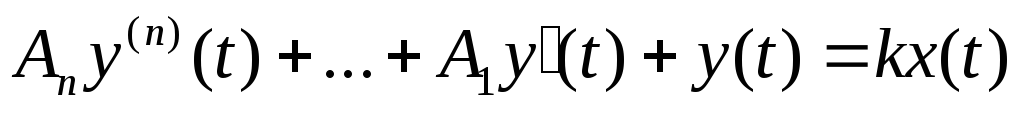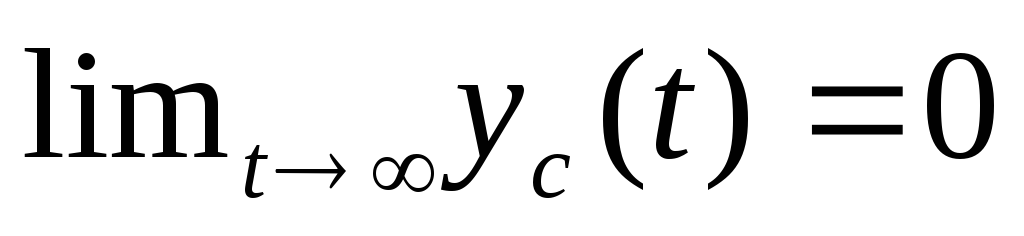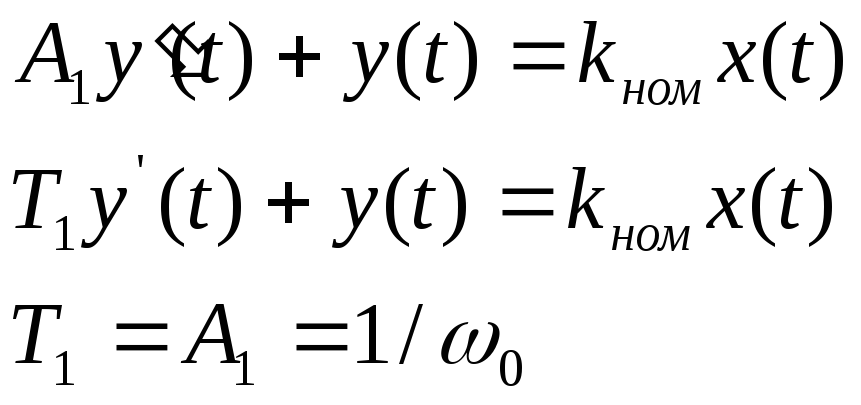Способ нормирования основной погрешности

Нормирование погрешностей средств измерений Классы точности

Основные погрешности средств измерения нормируются путем задания пределов допускаемой основной погрешности, при которой средство измерения (СИ) по техническим требованиям может быть допущено к применению.

Для того чтобы оценить погрешность, которую внесет данное СИ в конечный результат, пользуются предельными значениями погрешности для данного типа СИ.

Предел допускаемой основной абсолютной погрешности D может быть представлен одним из трех способов:

— постоянным для любых значений X числом, характеризующим аддитивную погрешность,

— в виде двухчленной формулы, включающей аддитивную и мультипликативную погрешности,

— в виде уравнения

При сложной зависимости (6.3) допускается представлять погрешность в виде графика и таблицы.

Пределы допускаемой относительной погрешности для случая (6.1) в процентах выражают формулой

(6.4)

для случая (6.2) – формулой

где Хк – предел измерений;

— имеет смысл приведенной погрешности в конце диапазона измерений (при Х=Хк);

— имеет смысл приведенной погрешности в начале диапазона измерений (при Х = 0), причем c > d.

Предел допускаемой приведенной погрешности в процентах выражается формулой

(6.5)

где р – отвлеченное положительное число.

Согласно ГОСТ 8.401-80 для указания нормированных пределов допускаемых погрешностей значения р, q, с, d выражаются в процентах и выбираются из ряда чисел: (1;1,5;2;2,5;3;4;5 и 6) ´10n , где n=+1;0;-1;-2;-3 и т.д.

В настоящее время в эксплуатации большое число средств измерений, метрологические характеристики которых нормируются на основе классов точности.

Класс точности – обобщенная характеристика средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими свойствами средств измерений, влияющими на точность, значение которых устанавливают в соответствующих стандартах.

Класс точности позволяет судить о том, в каких пределах находится погрешность средст измерений одного типа, но не характеризует точности измерений, выполняемых такими средствами, так как погрешность зависит и от метода измерений, и от условий измерений и т.д.

С использованием чисел указанного выше ряда чисел разработаны следующие условные обозначения классов точности СИ, наносимые на них.

1. Класс точности указывают просто одним из чисел приведенного выше предпочтительного ряда р (например, 1,5). Это используют для СИ, у которых предел допускаемой приведенной погрешности постоянен (присутствует только аддитивная погрешность), как в (6.1), Xn в (6.5) выражена в единицах измеряемой величины. Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой или степенной (с показателем степени не более двух) шкалой.

2. Класс точности указывает числом из приведенного выше ряда, под которым ставится треугольная скобка, например, . Такое обозначение применяют для приборов с резко неравномерной шкалой, для которых Хn выражают в единицах длины шкалы (мм, см, условных делениях). В этом случае при измерении, кроме значения измеряемой величины, обязательно должен быть записан отсчет X в единицах длины шкалы и предел Хn в этих же единицах, иначе нельзя будет вычислить погрешность результата. Таким способом обозначают класс точности омметров.

3. Число, обозначающее класс точности, обводят кружком например, . Такое обозначение применяют для СИ, у которых предел допускаемой относительной погрешности постоянен во всем диапазоне измерений (имеется только мультипликативная погрешность, (a в (6.2) равна нулю) и его определяют по (6.4). Таким способом нормируют погрешности измерительных мостов, магазинов, масштабных преобразователей. При этом обычно указывают границы рабочего диапазона, для которых справедлив данный класс точности.

4. Класс точности обозначается двумя числами, записываемыми через косую черту, т. е. в виде условной дроби c/d, например, 0,02 / 0,01. Такое обозначение применяют для СИ, у которых погрешность нормирована по двухчленной формуле (6.2). Таким способом указывают классы точности цифровых вольтметров, высокоточных потенциометров постоянного тока и других высокоточных приборов.

Источник

Нормирование погрешностей СИ

Средства измерений можно использовать только тогда, когда известны их метрологические характеристики. Обычно указываются номинальные значения параметров средств измерений и допускаемые отклонения от них. Сведения о метрологических характеристиках приводятся в технической документации на средства измерений или указываются на них самих. Как правило, реальные метрологические характеристики имеют отклонения от их номинальных значений. Поэтому устанавливают границы для отклонений реальных метрологических характеристик от номинальных значений – нормируют их. Нормирование метрологических характеристик средств измерений позволяет избежать произвольного установления их характеристик разработчиками.

C помощью нормируемых метрологических характеристик решаются следующие основные задачи:

— предварительный расчет с их помощью погрешностей результатов технических измерений (до проведения измерений);

— выбор средств измерений по заданным характеристикам их погрешностей.

Нормирование характеристик СИ проводится в соответствии с положениями стандартов. Например, ГОСТ 8.009-84 «ГСИ. Нормируемые метрологические характеристики средств измерений». Соответствие средств измерений установленным для них нормам делает эти средства взаимозаменяемыми.

Одной из важнейших метрологических характеристик СИ является их погрешность, знание которой необходимо для оценивания погрешности измерения.

Необходимо отметить, что погрешность СИ является только одной из составляющих погрешности результата измерений, получаемого с использованием данного СИ. Другими составляющими являются погрешность метода измерений и погрешность оператора, проводящего измерения.

Погрешности средств измерений могут быть обусловлены различными причинами:

— неидеальностью свойств средства измерений, то есть отличием его реальной функции преобразования от номинальной;

— воздействием влияющих величин на свойства средств измерений;

— взаимодействием средства измерений с объектом измерений — изменением значения измеряемой величины вследствие воздействия средства измерения;

— методами обработки измерительной информации, в том числе с помощью средств вычислительной техники.

Погрешности конкретных экземпляров СИ устанавливают только для эталонов, для остальных СИ вся информация об их погрешностях представляет собой те нормы, которые для них установлены. Нормирование погрешностей изложено в Рекомендации 34 МОЗМ «Классы точности средств измерений» и в ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования ».

В основе нормирования погрешностей средств измерений лежат следующие основные положения.

1. В качестве норм указывают пределы допускаемых погреш-ностей, включающие в себя систематические и случайные составляющие.

Под пределом допускаемой погрешности понимается наибольшее значение погрешности средства измерений, при котором оно еще признается годным к применению. Обычно устанавливают пределы, т.е. зоны, за которую не должна выходить погрешность. Данная норма отражает то положение, что средства измерений можно применять с однократным считыванием показаний.

2. Порознь нормируют все свойства СИ, влияющие на их точность: отдельно нормируют основную погрешность, по отдельности – все дополнительные погрешности и другие свойства, влияющие на точность измерений. При выполнении данного требования обеспечивается максимальная однородность средств измерений одного типа, то есть близкие значения дополнительных погреш-ностей, обусловленных одними и теми же факторами. Это дает возможность заменять один прибор другим однотипным без возможного увеличения суммарной погрешности.

Пределы допускаемых погрешностей средств измерения применяются как для абсолютной, так и для относительной погрешности.

Пределы допускаемой абсолютной погрешности устанавливают по формуле D = ± а для аддитивной погрешности. Для мультипликативной погрешности они устанавливаются в виде линейной зависимости

где х – показание измерительного прибора, а и b – положительные числа, не зависящие от х..

Предел допускаемой относительной погрешности (в относительных единицах) для мультипликативной погрешности устанавливают по формуле

Для аддитивной погрешности формула имеет вид:

d = D / х = ± [ c + d ( x_k / x – 1)]

где х_{k —} конечное значение диапазона измерений прибора; c и d — относительные величины.

Первое слагаемое в этой формуле имеет смысл относительной погрешности при х = х_k , второе — характеризует рост относительной погрешности при уменьшении показаний прибора. Пределы допускаемой приведенной погрешности(в процентах) следует устанавливать по формуле

где х_N – нормирующее значение; р — отвлеченное положительное число из ряда 1; 1,5; 2; 2,5; 4; 5; 6, умноженное на 10 n ( n = 1, 0, -1, -2 и т.д.)

Нормирующее значение принимается равным: конечному значению шкалы (если 0 находится на краю шкалы), сумме конечных значений шкалы (если 0 внутри шкалы), номинальному значению измеряемой величины, длине шкалы.

Источник

12. Способы нормирования погрешностей си. Нормирование основной и дополнительной погрешностей.

Класс точности средства измерения– основная интегральная метрологическая характеристика средства измерения, дающая предел основной погрешности.

В некоторых случаях класс точности задает и дополнительные погрешности, и другие метрологические характеристики. Значение класса точности выбирают из некоторого числового ряда:

Пример: 0.1 1.5 2.5 0.5/0.2 4- худший класс точности

У электронных осциллографов класс точности отражает другую величину.

Нормирование – задание номинальной характеристики для данного типа средства измерения и допускаемых отклонений для данного результата.

Тип средства измерения– совокупность средств измерений одного и того же назначения, основанная на одном и том же принципе, имеющие одинаковую конструкцию и выполненные по одной технологической документации.

Поверка – это выяснение соответствия данного средства измерения своему классу точности.

2 способа поверки – 1. Метод сравнения

2. Метод сличения

1. ОМ – образцовая мера

СИ – поверяемое средство измерения

На ходе ОМ формируется ФВ заданного значения с необходимой точность, причем погрешность ОМ пренебрежимо мала по сравнению с погрешностью СИ.

.

х_{вых си}СИ- поверяемое ср-во измерения

ОСИ– образцовое СИ

х_{вых оси}И – источник ФВ

Динамический режим может быть описан:

Переходные и импульсно-переходные характеристики

Поведение средства измерения в динамическом режиме может быть описано линейным неоднородным дифференциальным уравнением с постоянными коэффициентами.

Пусть статическая погрешность равна 0.

A_i– описывает характер поведения СИ

Общее решение невозможно. Удобно рассмотреть поведение средства измерения отдельно для переходного и установившегося режима.

y_c(t)- общее решение соответствующего однородного дифф. уравнения или свободные колебания (переходный режим СИ)

y_в(t) – частное решение неоднородного дифф. ур-ния, описывающее установившийся режим, т.е. режим вынужденных колебаний.

Для устойчивых СИ, свободные колебания носят затухающий характер, т.е. при увеличении времини приводит к окончанию свободных колебаний

Время установления показаний – выбирается таким, чтобы режим свободных колебаний уже закончился, тогда выходная величина y(t)=y_в(t)

В случае если дифф. уравнение, описывающее СИ имеет высокий порядок, то СИ разбивается на динамические звенья младших порядков.

Динамическое звено первого порядка.

T₁– постоянная времени;ω₀– некоторая граничная частота данного динамического звена.

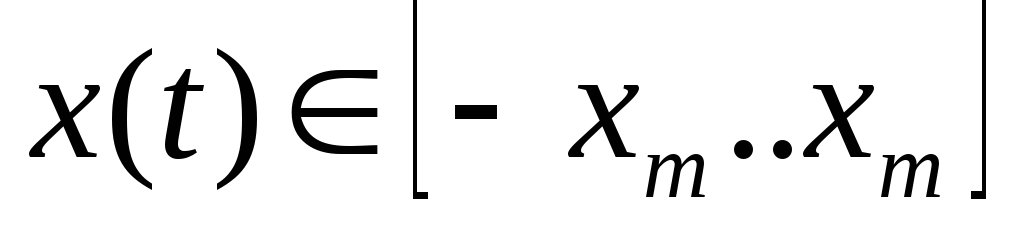
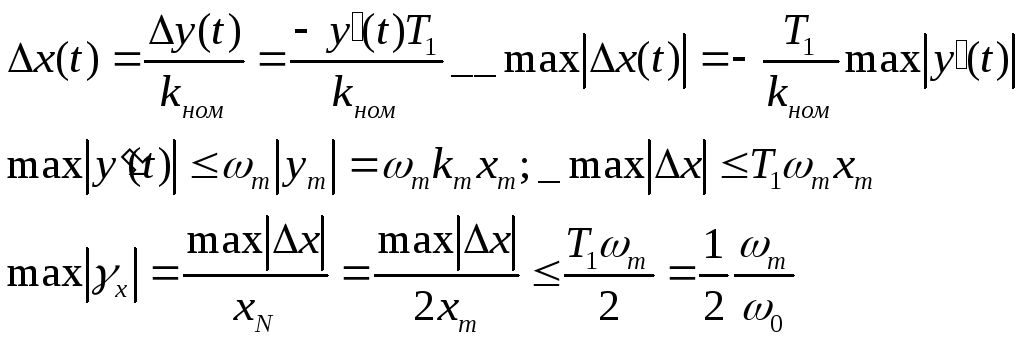
Пусть , а также имеет ограниченный спектр.

k_m–maxзначение преобр. звена первого порядка

Дает завышенную оценку, поэтому им следует пользоваться при малых значениях отношения частот (ω_m/ ω₀)

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник