Способ нормального сечения это

Способ нормального сечения это

Способ нормального сечения заключается в том, что цилиндр или призма пересекаются плоскостью, перпендикулярной образующим цилиндра или ребрам призмы.

Способ нормального сечения применяется в том случае, если основание призмы не является плоскостью уровня, а основание цилиндра – окружностью.

Строится сечение цилиндра или призмы этой плоскостью и определяется его натуральная величина. Затем сечение спрямляется, и перпендикулярно спрямленному нормальному сечению проводятся прямые, соответствующие образующим цилиндра или ребрам призмы, и на этих прямых откладываются натуральные величины образующих или ребер.

Соединив концы образующих или ребер плавной кривой или ломаной линией, получают развертку боковой поверхности цилиндра или призмы.

Рассмотрим применение этого способа для призматических поверхностей на примере треугольной призмы, ребра которой являются фронтальными линиями уровня (рис. 155).

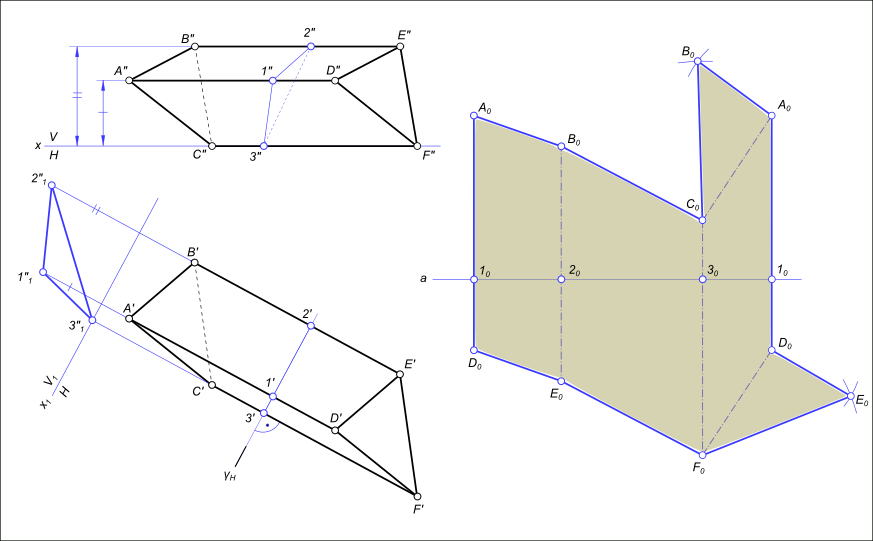
Так как боковые ребра призмы являются фронтальными линиями уровня, они проецируются на фронтальную плоскость проекций в натуральную величину. Тогда фронтально – проецирующая плоскость δ(δ₂), перпендикулярная к боковым ребрам, определит нормальное сечение I–II–III призмы. Способом плоскопараллельного движения определена его натуральная величина I’₁–II’₁–III’₁.

Для построения развертки призмы строится спрямленное нормальное сечение I₀–II₀–III₀. Для этого нужно отложить на произвольной прямой натуральные величины сторон нормального сечения, а затем через точки I₀, II₀ и III₀ нужно провести прямые, перпендикулярные к этой прямой. На этих прямых откладываются натуральные величины ребер:

Затем точки A₀, B₀, C₀, A₀ и точки A’₀, B’₀, C’₀, A’₀ соединяются прямыми линиями. К полученной развертке боковой поверхности призмы пристраиваются натуральные величины двух ее оснований:

Если боковые ребра данной призмы занимают произвольное расположение относительно плоскостей проекций, то нужно предварительно преобразовать их в линии уровня.

Рассмотрим построение разверток цилиндрических поверхностей на примере построения развертки боковой поверхности кругового цилиндра, ось i которого является фронтальной линией уровня (рис. 156).

Так же, как и в случае призмы, построено нормальное сечение цилиндра фронтально — проецирующей плоскостью α(α₂), перпендикулярной оси цилиндра и определена его натуральная величина – окружность радиусом r. Эта окружность разбита на шесть равных частей точками I, II, III, IV, V и VI. Далее строится спрямленное нормальное сечение I₀-II₀-III₀-IV₀-V₀-VI₀-I₀, длина которого равна 2πr. Через точки I₀,II₀,III₀,IV₀,V₀,VI₀ и I₀ проводятся прямые, перпендикулярные спрямленному нормальному сечению, и на них откладываются натуральные величины образующих цилиндра:

Точки A₀, B₀, C₀…и точки A’₀, B’₀, C’₀…соединяются плавными кривыми линиями, которые будут развертками верхнего и нижнего оснований цилиндра.

Если образующие цилиндра являются прямыми общего положения, то следует преобразовать их так, чтобы они стали линиями уровня.

Источник

Способ нормального сечения

Этот способ применяется для построения разверток призматических и цилиндрических поверхностей.

Построение сводится к многократному построению натурального вида трапеций, из которых состоит данная призматическая поверхность, или призматическая поверхность, вписанная (или описанная) в данную цилиндрическую поверхность и заменяющая ее. Если, в частности, призматическая или цилиндрическая поверхности ограничены параллельными основаниями, то трапеции, на которые разбивается поверхность, обращаются в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или нет плоскости оснований боковым ребрам или образующим поверхности.

Построение трапеций или параллелограммов проще всего произвести по их основаниям и высотам, причем необходимо также знать отрезки оснований, на которые они делятся высотой. Поэтому для построения развертки призматической или цилиндрической поверхности необходимо предварительно определить натуральный вид нормального сечения данной поверхности. Стороны этого сечения и будут высотами трапеций или параллелограммов, из которых состоит поверхность. Этот способ называется СПОСОБОМ НОРМАЛЬНОГО СЕЧЕНИЯ.

Пример. Построить развертку поверхности треугольной наклонной призмы АВСDEF (рис. 167).

Боковые ребра призмы имеют горизонтальное расположение. Пересечем данную призму плоскостью a(a_H), перпендикулярной к боковым ребрам, и построим проекции фигуры сечения — треугольник 1-2-3 (рис. 167).

Определим натуральные величины сторон треугольника 1-2-3 способом замены плоскостей проекций: меняем фронтальную плоскость проекций V на новую V₁ таким образом, чтобы плоскость a стала плоскостью уровня, для чего ось x₁ новой системы плоскостей проекций H/V₁ проводим параллельно a_H. Тогда на новой фронтальной плоскости V₁ получим натуральную величину треугольника 1-2-3 (рис. 167).

На произвольной горизонтальной прямой построим отрезок, равный периметру треугольника 1-2-3 (рис. 167). Отрезок 1-1 можно считать разверткой нормального сечения призмы. Из всех точек (1,2,3,1) этого отрезка проводим прямые, перпендикулярные к нему, на которых откладываем отрезки боковых ребер (натуральные величины), беря их с горизонтальной проекции, так как они являются горизонталями. Концы отложенных отрезков соединяем прямыми СА, АВ, FD, . Фигура CABCFEDF представляет собой развертку боковой поверхности призмы.

Полная развертка призмы показана на рис. 167. Для построения граней основания из точек В и С проводим дуги окружностей радиусами, равными соответственно натуральным величинам ребер ВА и СА. Пересечение дуг дает точку А. Аналогичным образом найдена точка D.

Способ раскатки

Способ раскатки рекомендуется для построения развертки цилиндрической поверхности, когда ее образующие являются прямыми уровня, то есть параллельными одной из плоскостей проекций.

Рассмотрим данный способ на примере эллиптического цилиндра с круговым основанием, которое проецируется на горизонтальную плоскость проекций без искажения (в натуральную величину).

Построение развертки данного цилиндра выполняем в следующей последовательности (рис. 168):

1. Делим окружность основания цилиндра на 12 равных частей.

2. Вписываем в цилиндр призму, боковые ребра которой совпадают с образующими цилиндра, проходящими через точки деления основания (рис. ).

3. Принимаем за плоскость развертки фронтальную плоскость g (g_H), которая проходит через ребро призмы, совпадающее с очерковой образующей цилиндра (1).

4. Находим натуральную величину первой грани, проходящей через ребро 1, для чего вращаем ее вокруг фронтали 1”до уровня этой фронтали. При этом точка 2”переместится по направлению, перпендикулярному к этой фронтали в положение 2, которое найдем, если из точки 1”это направление засечем отрезком 1’2′.

Из точки 3”проводим также перпендикуляр к ребру 1(1”) и находим точку 3, отсекая этот перпендикуляр из точки 2 отрезком 2’3′ и т.д.

Соединяя найденные точки плавной кривой получим фигуру развертки, которую можно представлять себе как отпечаток цилиндра, полученный путем его качения по фронтальной плоскости, проходящей через образующую 1.

Источник

Способ нормального сечения

Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ нормального сечения применяется для развертки призматических гранных поверхностей. Отличительная особенность данного способа является построение сечения призмы плоскостью нормальной (перпендикулярной) по отношению к ее боковым ребрам. При последующем развертывании призмы линия нормального сечения выстраивается в прямую линию и используется для откладывания от нее натуральной величины отрезков боковых ребер.

Построить развертку наклонной трехгранной призмы ABCDEF, иcпользуя способ нормального сечения.

Построим сечение заданной призмы вспомогательной плоскостью γ_H перпендикулярной к ее боковым ребрам и горизонтальной плоскости проекций H. Методом перемены плоскостей проекций определяем действительную величину сторон Δ123. В произвольном месте эпюра проводим горизонтально прямую a. От точки 1₀, отмеченной на этой прямой, откладываем отрезки [1₀2₀], [2₀3₀], [3₀1₀], конгруентные сторонам Δ123. Через точки 1₀2₀3₀ и 1₀ проводим прямые перпендикулярные к прямой a, и откладываем на них от точек 1₀2₀3₀ и 1₀ отрезки, конгруентные соответствующим действительным величинам отрезков боковых ребер. Полученные точки A₀B₀C₀A и D₀E₀ F₀D₀ соединяем прямыми. Ребра AD, BE, и CF параллельны плоскости H, поэтому на нее они проецируются в действительную величину. Плоская фигура A₀B₀C₀A₀D₀E₀F₀D₀ — развертка боковой поверхности призмы. К ней пристроены основания призмы ΔA₀B₀C₀ и ΔD₀E₀F₀.

Способ нормального сечения применяется также для получения развертки цилиндрической поверхности: Развертка цилиндра

Источник

Способ нормального сечения

1. Для получения нормального сечения проводится плоскость
перпендикулярная к боковым ребрам призмы.

2. Определяется натуральная величина нормального сечения. Стороны этого сечения определяют расстояние между боковыми ребрами, т.е. ширину граней.

3. Нормальное сечение разворачивается в прямую и через концы отрезков проводятся ребра призмы, которые перпендикулярны построенной прямой, а следовательно и к периметру 1,2,3 сечения.

4. На проведенных ребрах откладываются длины отрезков боковых ребер, заключенных между линией сечения и основаниями. Полученные точки соединяются последовательно между собой.

Пример 4. Построить полную развертку наклонной треугольной призмы (рис. 12.5).

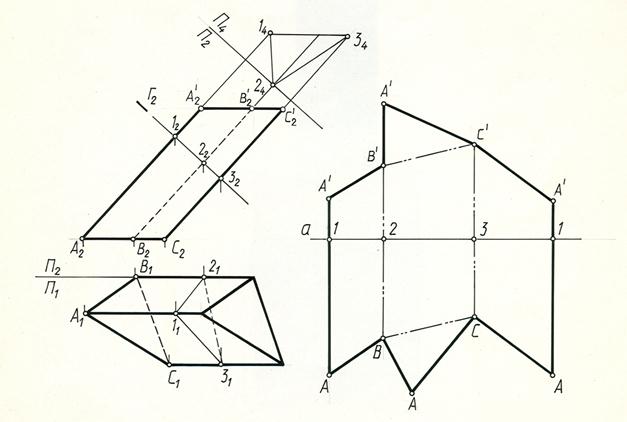
Призма расположена относительно плоскостей проекций так, что ее боковые ребра параллельны фронтальной плоскости проекций и проецируются на П₂ в натуральную величину. Стороны основания проецируется без искажения на плоскость П₁. Пересечем призму в произвольном месте плоскостью Г перпендикулярной боковым ребрам.

В нашем примере эта плоскость является фронтально-проецирующей плоскостью и пересекает призму по треугольнику 1 2 3. (1₂2₂3₂, 1₁2₁3₁) Стороны треугольника определяют расстояние между боковыми ребрами. Определяем натуральную величину сечения (треугольник A₄B₄C₄), используя способ замены плоскостей проекций. Стороны нормального сечения; последовательно отложим на прямой а: 1-2=1₄-2₄, 2-3=2₄-3₄, 3-1=3₄-1₄. Полученный отрезок 1-1 равен периметру нормального сечения.

Через точки 1, 2, 3 проведем прямые перпендикулярные к, развертке периметра сечения и на них отложим натуральную величину боковых ребер 1А=1₂А₂ и 1А’=1₂А₂‘ , 2В=2₂В₂ и 2В’=2₂В₂‘, ЗС=3₂С₂ и ЗС’=3₂С₂‘ и т.д. Соединив концы отложенных отрезков, получим развертку боковой поверхности призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований, используя натуральные величины их сторон.

Источник

8.2.2. Способ «нормального» сечения

Способом «нормального» сечения строятся развертки призматических и цилиндрических поверхностей. Построение разверток приводит, в общем случае, к многократному построению натурального вида трапеций, из которых состоит боковая поверхность призмы или призматическая поверхность вписанная (описанная) в цилиндрическую и заменяющая ее. Если призматическая или цилиндрическая поверхность ограничены параллельными основаниями, то боковые грани будут представлены параллелограммами или прямоугольниками, в зависимости от того, перпендикулярны или нет боковые ребра или образующие поверхности плоскостям оснований.

Построение трапеций или параллелограммов можно производить различными способами. Например, можно разбить их на треугольники, определить натуральную величину этих треугольников, и, пристроив один треугольник к другому, получить натуральную величину трапеции (параллелограмма).

Однако проще всего построить натуральные величины трапеций или параллелограммов по их основаниям и высотам. При этом необходимо знать отрезки a, b, c, d оснований, на которые они делятся высотой е (рисунок 171).

П

оэтому для построения развертки призматической или цилиндрической поверхности нужно предварительно определить натуральный вид «нормального» сечения данной поверхности. Стороны этого сечения, в случае призматической поверхности, и будут высотами трапеций или параллелограммов, составляющих боковую поверхность. В случае цилиндрической поверхности высотами будут хорды, стягивающие дуги «нормального» сечения, на которые разбивают кривую, ограничивающую это сечение.

Пример 1. Построить полную развертку поверхности треугольной призмы ABCDEF и нанести на развертку точку М, принадлежащую поверхности (рисунок 172).

Пусть призма расположена так, что ее боковые ребра являются фронталями и проецируются на виде спереди (фронтальной проекции) в натуральную величину.

В произвольном месте рассечем призму фронтально проецирующей плоскостью Б, перпендикулярной («нормальной») ее ребрам. Построив натуральный вид 1-2-3 этого сечения, находим натуральные величины 1-2, 2-3 и 3-1 высот параллелограммов, из которых состоит боковая поверхность призмы.

П 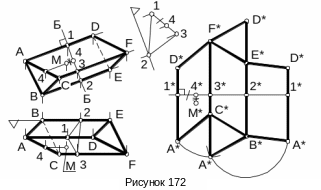оскольку боковые ребра призмы параллельны между собой, а стороны «нормального» сечения им перпендикулярны, то из свойства сохранения углов на развертке следует, что на развертке боковые ребра так же будут параллельны между собой, а стороны «нормального» сечения, будучи перпендикулярными им, развернутся в прямую линию.

Для построения развертки нужно на произвольной прямой (в нашем примере – горизонтальной) отложить натуральные величины 1-2, 2-3 и 3-1 сторон «нормального» сечения. Через полученные точки 1*, 2*, 3* и 1* проведем прямые, перпендикулярные к прямой «нормального» сечения. Теперь отложим на этих перпендикулярах по обе стороны от прямой 1*-2*-3*-1* отрезки, на которые делятся боковые ребра призмы секущей плоскостью Б. Соединяя отрезками прямых полученные точки A*, B*, C*, D*, E* и F*, получим развертку боковой поверхности призмы. Присоединив к ней оба основания-треугольника, построенные по трем известным сторонам, получим полную развертку призмы.

Для построения на развертке некоторой точки М, принадлежащей поверхности призмы, нужно отложить на прямой 1*-2*-3*-1* отрезок 1*-4*=1-4. Затем через точку 4* провести прямую, параллельную боковым ребрам и на этой прямой отложить отрезок 4*-М*=4-М.

Если бы боковые ребра призмы не были прямыми уровня, как в нашем примере, то нужно было бы предварительно преобразовать чертеж так, чтобы они стали прямыми уровня.

Пример 2. Построить развертку боковой поверхности эллиптического цилиндра (рисунок 173).

Несмотря на то, что цилиндрические поверхности являются развертывающимися, практически строят их приближенные развертки, заменяя цилиндр вписанной призматической поверхностью.

В 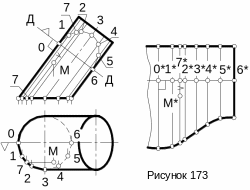нашем примере поверхность имеет фронтальную плоскость симметрии, что позволяет построить развертку только половины поверхности.

Для построения «нормального» сечения, проведем фронтально проецирующую плоскость Д перпендикулярно образующим цилиндрической поверхности. При помощи построения дополнительного вида определим натуральный вид половины «нормального» сечения цилиндрической поверхности. Разделив на шесть равных частей половину горизонтального основания цилиндра, перенесем полученные точки на дугу полуэллипса, являющегося половиной «нормального» сечения.

Проведем на поверхности цилиндра образующие, соответствующие точкам деления «нормального» сечения. При этом поверхность половины цилиндра разобьется на шесть трапеций, поскольку плоскости оснований не параллельны между собой. Основаниями трапеций будут образующие (натуральные величины которых имеются на виде спереди), а высотами – хорды, стягивающие дуги полу эллипса «нормального» сечения.

Дальнейшее построение развертки производится так же, как и в предыдущем примере, только вершины построенных на развертке трапеций соединяем не отрезками прямых, а плавными кривыми. Одна из этих кривых в нашем примере является прямой линией, так как наклонное основание цилиндра перпендикулярно его образующим.

Для построения на развертке некоторой точки М, принадлежащей поверхности цилиндра, нужно провести на поверхности через эту точку вспомогательную образующую. Затем построить соответствующую ей образующую на развертке и на ней отложить от линии сечения расстояние до точки М. При этом 7*-М*=7-М.

П 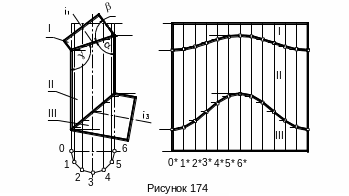ример 3. Построить развертку цилиндрического трубопровода кругового сечения, состоящего из трех элементов, расположенных параллельно фронтальной плоскости (рисунок 174).

Для более рационального использования листового материала, из которого будет изготавливаться развертка, проделаем следующее. Мысленно отделим элементы I и III от элемента II и повернем их относительно своих осей i1 и i3 на 180˚. Если теперь приставить обратно элементы I и III так, чтобы совпали эллипсы, по которым пересекаются эти элементы, то все три элемента составят один цилиндр (изображенный штрих пунктирной линией), на поверхности которого проведены два эллипса.

Справедливость вышесказанного доказать несложно. На самом деле α+γ=180°, но α=β ввиду равенства диаметров труб, поэтому β+ γ=180°.

Таким образом нужно построить развертку спрямленной трубы в виде прямоугольника и нанести на нее точки принадлежащие эллипсам, которые затем соединить плавными кривыми линиями.

В случае, когда оси отдельных элементов трубопровода расположены не в одной плоскости (как в данном примере), развертка строится аналогично приведенному примеру.

Источник